Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 64561 by aliesam last updated on 19/Jul/19

Commented by mathmax by abdo last updated on 20/Jul/19

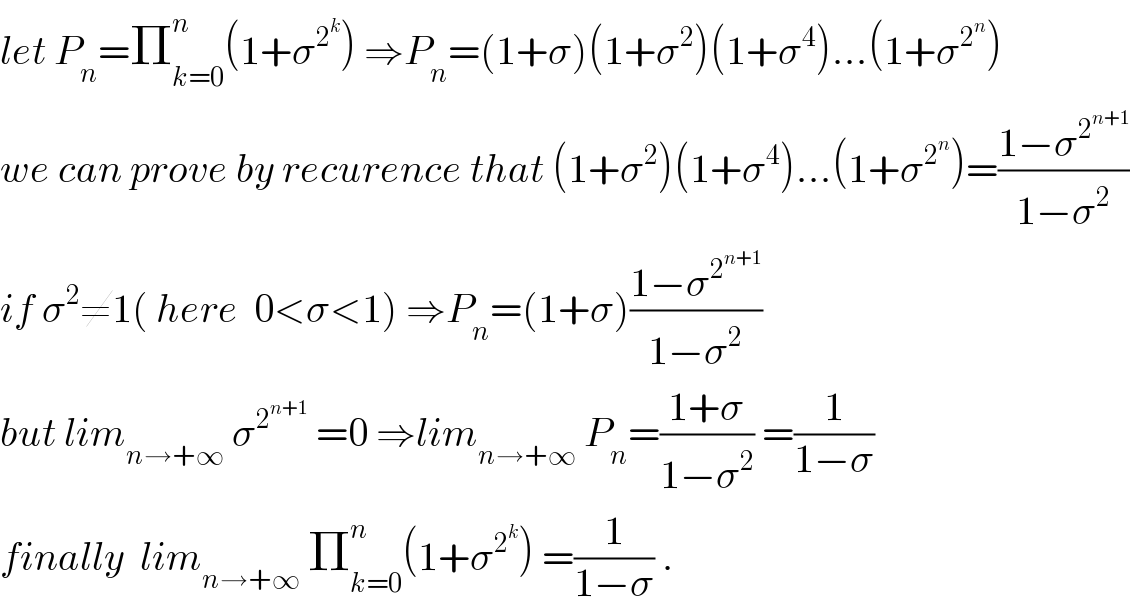
let P_n =Π_(k=0) ^n (1+σ^2^k ) ⇒P_n =(1+σ)(1+σ^2 )(1+σ^4 )...(1+σ^2^n ) we can prove by recurence that (1+σ^2 )(1+σ^4 )...(1+σ^2^n )=((1−σ^2^(n+1) )/(1−σ^2 )) if σ^2 ≠1( here 0<σ<1) ⇒P_n =(1+σ)((1−σ^2^(n+1) )/(1−σ^2 )) but lim_(n→+∞) σ^2^(n+1) =0 ⇒lim_(n→+∞) P_n =((1+σ)/(1−σ^2 )) =(1/(1−σ)) finally lim_(n→+∞) Π_(k=0) ^n (1+σ^2^k ) =(1/(1−σ)) .

$${let}\:{P}_{{n}} =\prod_{{k}=\mathrm{0}} ^{{n}} \left(\mathrm{1}+\sigma^{\mathrm{2}^{{k}} } \right)\:\Rightarrow{P}_{{n}} =\left(\mathrm{1}+\sigma\right)\left(\mathrm{1}+\sigma^{\mathrm{2}} \right)\left(\mathrm{1}+\sigma^{\mathrm{4}} \right)...\left(\mathrm{1}+\sigma^{\mathrm{2}^{{n}} } \right) \\ $$$${we}\:{can}\:{prove}\:{by}\:{recurence}\:{that}\:\left(\mathrm{1}+\sigma^{\mathrm{2}} \right)\left(\mathrm{1}+\sigma^{\mathrm{4}} \right)...\left(\mathrm{1}+\sigma^{\mathrm{2}^{{n}} } \right)=\frac{\mathrm{1}−\sigma^{\mathrm{2}^{{n}+\mathrm{1}} } }{\mathrm{1}−\sigma^{\mathrm{2}} } \\ $$$${if}\:\sigma^{\mathrm{2}} \neq\mathrm{1}\left(\:{here}\:\:\mathrm{0}<\sigma<\mathrm{1}\right)\:\Rightarrow{P}_{{n}} =\left(\mathrm{1}+\sigma\right)\frac{\mathrm{1}−\sigma^{\mathrm{2}^{{n}+\mathrm{1}} } }{\mathrm{1}−\sigma^{\mathrm{2}} } \\ $$$${but}\:{lim}_{{n}\rightarrow+\infty} \:\sigma^{\mathrm{2}^{{n}+\mathrm{1}} } \:=\mathrm{0}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{P}_{{n}} =\frac{\mathrm{1}+\sigma}{\mathrm{1}−\sigma^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{1}−\sigma} \\ $$$${finally}\:\:{lim}_{{n}\rightarrow+\infty} \:\prod_{{k}=\mathrm{0}} ^{{n}} \left(\mathrm{1}+\sigma^{\mathrm{2}^{{k}} } \right)\:=\frac{\mathrm{1}}{\mathrm{1}−\sigma}\:. \\ $$

Answered by JDamian last updated on 20/Jul/19

The answer is (1/(1−δ)) let P_n =Π_(k=0) ^(n) (1+δ^2^k ). It is easy to show that P_n is actually the sum of the following geometric progession, which: − first value is 1. − common ratio is δ. − length is 2^n . P_n =Σ_(k=0) ^(2^n −1) δ^k ∀δ 0<δ<1 lim_(n→∞) P_n =(1/(1−δ))

$${The}\:{answer}\:{is}\:\frac{\mathrm{1}}{\mathrm{1}−\delta} \\ $$$$ \\ $$$${let}\:{P}_{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\Pi}}\left(\mathrm{1}+\delta^{\mathrm{2}^{{k}} } \right).\:{It}\:{is}\:{easy}\:{to}\:{show}\:{that} \\ $$$${P}_{{n}} \:{is}\:{actually}\:{the}\:\boldsymbol{{sum}}\:\boldsymbol{{of}}\:\boldsymbol{{the}}\:\boldsymbol{{following}} \\ $$$$\boldsymbol{{geometric}}\:\boldsymbol{{progession}},\:{which}: \\ $$$$−\:{first}\:{value}\:{is}\:\mathrm{1}. \\ $$$$−\:{common}\:{ratio}\:{is}\:\delta. \\ $$$$−\:{length}\:{is}\:\mathrm{2}^{{n}} . \\ $$$$ \\ $$$${P}_{{n}} =\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}^{{n}} −\mathrm{1}} {\sum}}\delta^{{k}} \:\:\forall\delta\:\:\:\mathrm{0}<\delta<\mathrm{1} \\ $$$$\underset{{n}\rightarrow\infty} {{lim}}\:{P}_{{n}} =\frac{\mathrm{1}}{\mathrm{1}−\delta} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com