
Question Number 63790 by rajesh4661kumar@gamil.com last updated on 09/Jul/19
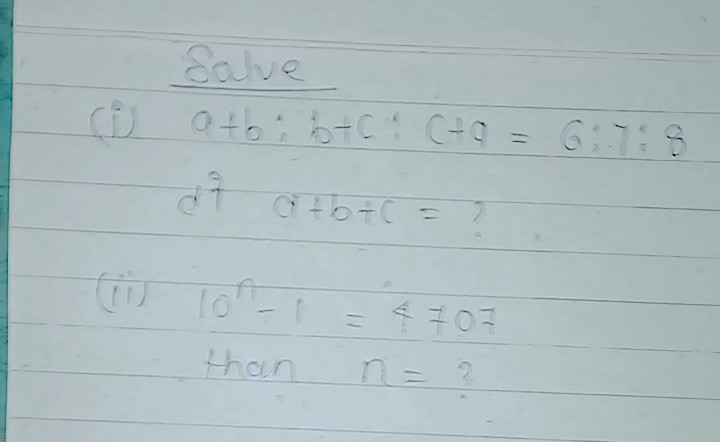
Answered by Hope last updated on 10/Jul/19
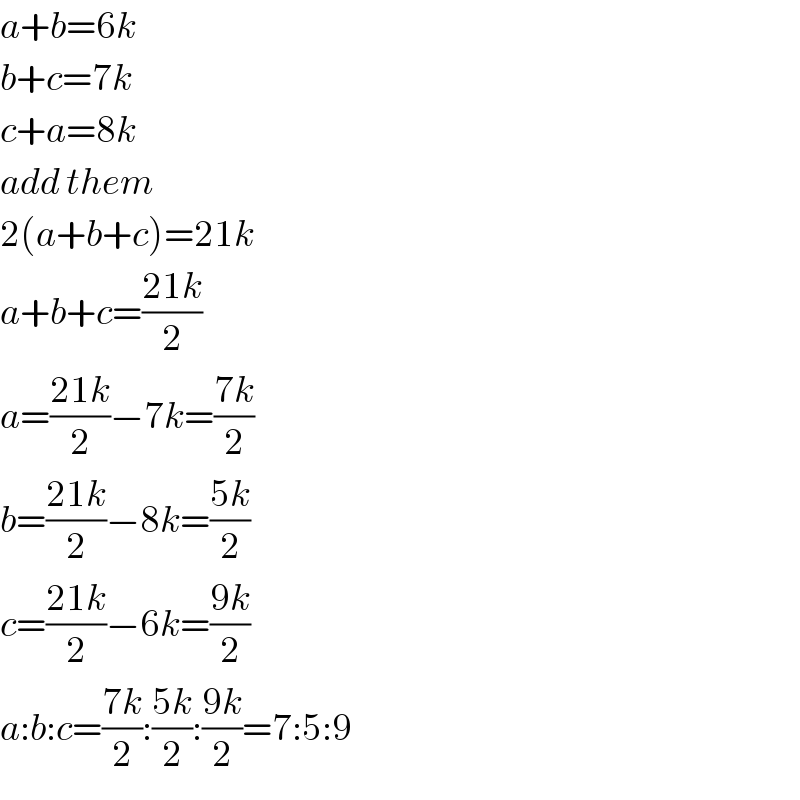
$${a}+{b}=\mathrm{6}{k} \\ $$$${b}+{c}=\mathrm{7}{k} \\ $$$${c}+{a}=\mathrm{8}{k} \\ $$$${add}\:{them} \\ $$$$\mathrm{2}\left({a}+{b}+{c}\right)=\mathrm{21}{k} \\ $$$${a}+{b}+{c}=\frac{\mathrm{21}{k}}{\mathrm{2}} \\ $$$${a}=\frac{\mathrm{21}{k}}{\mathrm{2}}−\mathrm{7}{k}=\frac{\mathrm{7}{k}}{\mathrm{2}} \\ $$$${b}=\frac{\mathrm{21}{k}}{\mathrm{2}}−\mathrm{8}{k}=\frac{\mathrm{5}{k}}{\mathrm{2}} \\ $$$${c}=\frac{\mathrm{21}{k}}{\mathrm{2}}−\mathrm{6}{k}=\frac{\mathrm{9}{k}}{\mathrm{2}} \\ $$$${a}:{b}:{c}=\frac{\mathrm{7}{k}}{\mathrm{2}}:\frac{\mathrm{5}{k}}{\mathrm{2}}:\frac{\mathrm{9}{k}}{\mathrm{2}}=\mathrm{7}:\mathrm{5}:\mathrm{9} \\ $$
Answered by Hope last updated on 10/Jul/19

$$\mathrm{10}^{{n}} −\mathrm{1}=\mathrm{4707} \\ $$$$\mathrm{10}^{{n}} =\mathrm{4708}= \\ $$$${n}={log}_{\mathrm{10}} \mathrm{4708} \\ $$
