
Question Number 63615 by aliesam last updated on 06/Jul/19
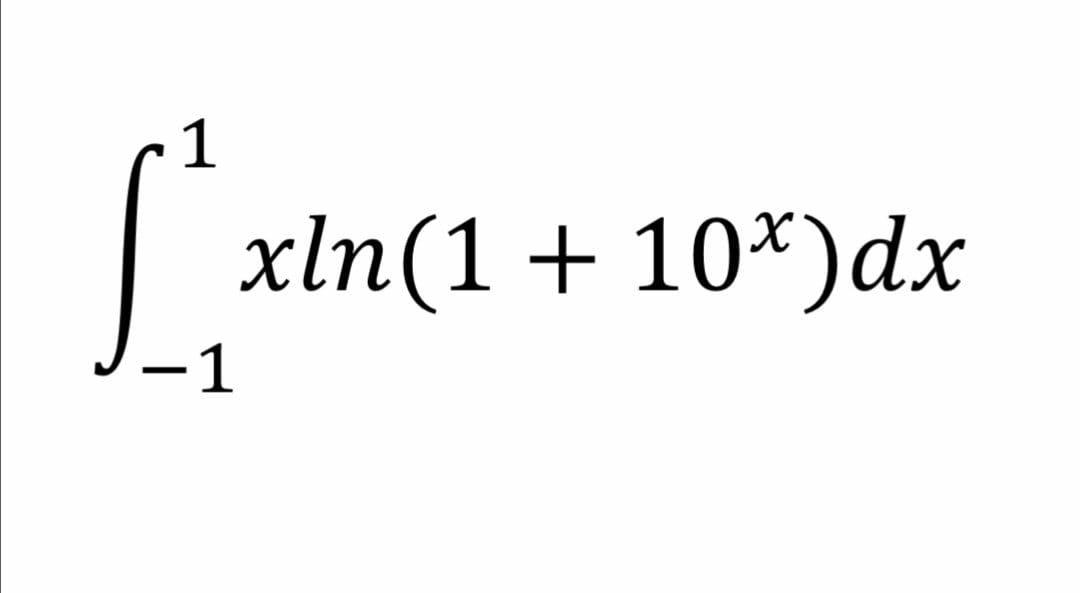
Commented by mathmax by abdo last updated on 06/Jul/19
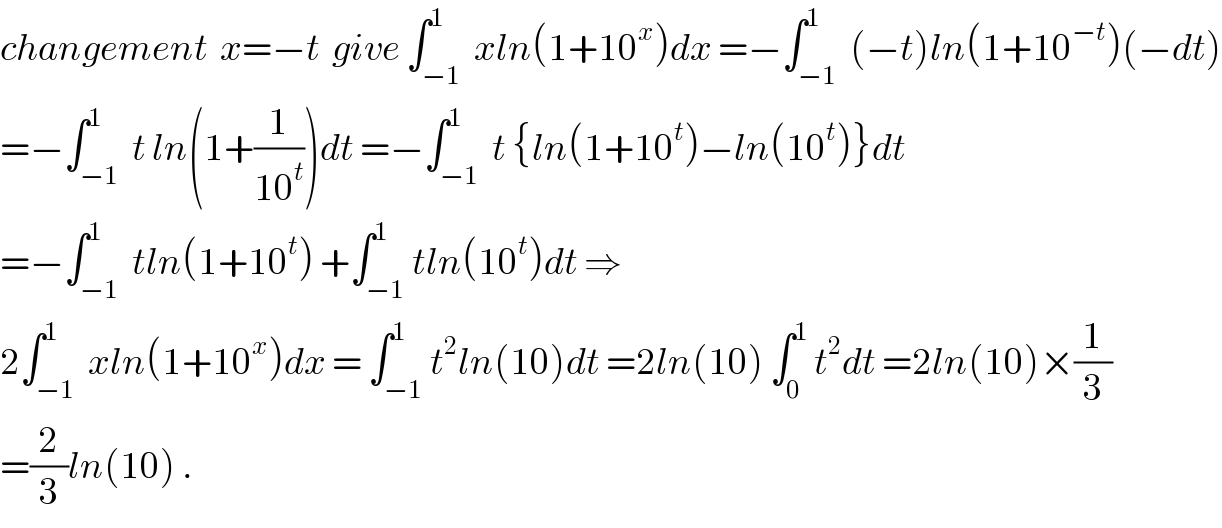
$${changement}\:\:{x}=−{t}\:\:{give}\:\int_{−\mathrm{1}} ^{\mathrm{1}} \:{xln}\left(\mathrm{1}+\mathrm{10}^{{x}} \right){dx}\:=−\int_{−\mathrm{1}} ^{\mathrm{1}} \:\left(−{t}\right){ln}\left(\mathrm{1}+\mathrm{10}^{−{t}} \right)\left(−{dt}\right) \\ $$$$=−\int_{−\mathrm{1}} ^{\mathrm{1}} \:{t}\:{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{10}^{{t}} }\right){dt}\:=−\int_{−\mathrm{1}} ^{\mathrm{1}} \:{t}\:\left\{{ln}\left(\mathrm{1}+\mathrm{10}^{{t}} \right)−{ln}\left(\mathrm{10}^{{t}} \right)\right\}{dt} \\ $$$$=−\int_{−\mathrm{1}} ^{\mathrm{1}} \:{tln}\left(\mathrm{1}+\mathrm{10}^{{t}} \right)\:+\int_{−\mathrm{1}} ^{\mathrm{1}} {tln}\left(\mathrm{10}^{{t}} \right){dt}\:\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\mathrm{2}\int_{−\mathrm{1}} ^{\mathrm{1}} \:{xln}\left(\mathrm{1}+\mathrm{10}^{{x}} \right){dx}\:=\:\int_{−\mathrm{1}} ^{\mathrm{1}} {t}^{\mathrm{2}} {ln}\left(\mathrm{10}\right){dt}\:=\mathrm{2}{ln}\left(\mathrm{10}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{\mathrm{2}} {dt}\:=\mathrm{2}{ln}\left(\mathrm{10}\right)×\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}{ln}\left(\mathrm{10}\right)\:. \\ $$
Commented by aliesam last updated on 06/Jul/19

$${god}\:{bless}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 06/Jul/19

$${you}\:{are}\:{welcome}. \\ $$
Commented by MJS last updated on 06/Jul/19

$$\mathrm{great}!\:\mathrm{but}\:\mathrm{of}\:\mathrm{course}\:\mathrm{the}\:\mathrm{final}\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\mathrm{10} \\ $$
Commented by Prithwish sen last updated on 06/Jul/19

$$\mathrm{excellent}\:\mathrm{sir}. \\ $$
