
Question Number 63570 by mr W last updated on 05/Jul/19
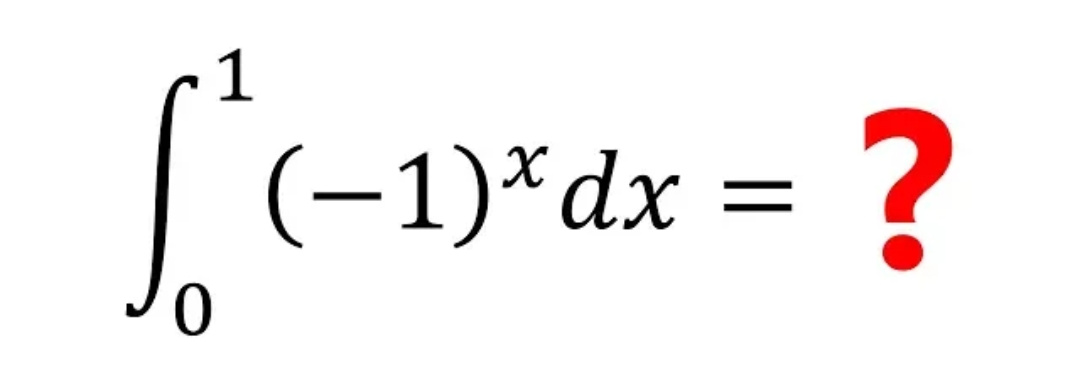
Commented by mathmax by abdo last updated on 05/Jul/19
![∫_0 ^1 (−1)^x dx =∫_0 ^1 e^(iπx) dx =[(1/(iπ)) e^(iπx) ]_0 ^1 =(1/(iπ)){ e^(iπ) −1} =((−2)/(iπ)) ⇒ ∫_0 ^1 (−1)^x dx = ((2i)/π)](Q63577.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{{x}} {dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{{i}\pi{x}} {dx}\:=\left[\frac{\mathrm{1}}{{i}\pi}\:{e}^{{i}\pi{x}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\mathrm{1}}{{i}\pi}\left\{\:{e}^{{i}\pi} −\mathrm{1}\right\}\:=\frac{−\mathrm{2}}{{i}\pi}\:\:\Rightarrow \\ $$$$\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(−\mathrm{1}\right)^{{x}} {dx}\:=\:\frac{\mathrm{2}{i}}{\pi} \\ $$
Commented by mr W last updated on 05/Jul/19

$${thank}\:{you}\:{sir}! \\ $$
Commented by mathmax by abdo last updated on 05/Jul/19
$${you}\:{are}\:{welcome}\:{sir}\:. \\ $$
Answered by MJS last updated on 05/Jul/19
![∫a^x dx=(a^x /(ln a)) +C ∫_0 ^1 (−1)^x dx=[(((−1)^x )/(ln −1))]_0 ^1 =−(2/(ln −1))=(2/π)i](Q63571.png)
$$\int{a}^{{x}} {dx}=\frac{{a}^{{x}} }{\mathrm{ln}\:{a}}\:+{C} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left(−\mathrm{1}\right)^{{x}} {dx}=\left[\frac{\left(−\mathrm{1}\right)^{{x}} }{\mathrm{ln}\:−\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} =−\frac{\mathrm{2}}{\mathrm{ln}\:−\mathrm{1}}=\frac{\mathrm{2}}{\pi}\mathrm{i} \\ $$
Commented by mr W last updated on 05/Jul/19

$${thanks}\:{sir}! \\ $$
Commented by MJS last updated on 05/Jul/19
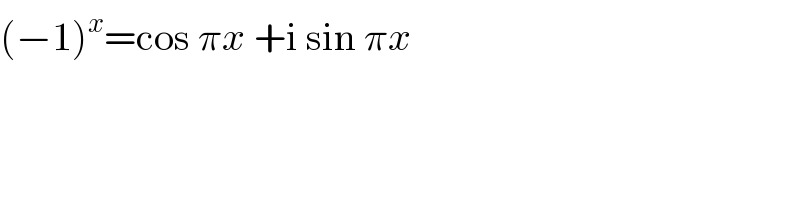
$$\left(−\mathrm{1}\right)^{{x}} =\mathrm{cos}\:\pi{x}\:+\mathrm{i}\:\mathrm{sin}\:\pi{x} \\ $$
