Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 63522 by Tawa1 last updated on 05/Jul/19

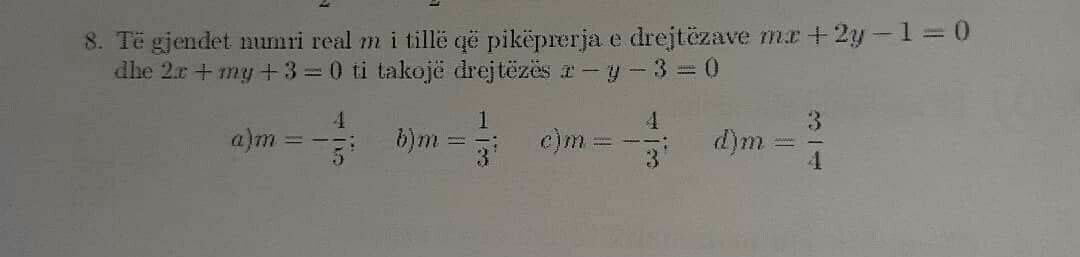
Commented by Tawa1 last updated on 05/Jul/19

Find the real parameter “m” such that cross cutting of mx + 2y - 1 = 0 and 2x + my + 3 = 0 give slopes equation belongs x - y - 3 = 0

Commented by MJS last updated on 05/Jul/19

(1) mx+2y−1=0 (2) 2x+my+3=0 (3) x−y−3=0 maybe I do not understand what to do, but we have 3 equations in 3 unknown, so we get an unique solution (1) ⇒ y=((1−mx)/2) (2) ⇒ x=((m+6)/(m^2 −4)) ⇒ y=−((3m+2)/(m^2 −4)) (3) ⇒ m=((10)/3) ⇒ x=((21)/(16))∧y=−((27)/(16))

$$\left(\mathrm{1}\right)\:{mx}+\mathrm{2}{y}−\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{2}{x}+{my}+\mathrm{3}=\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:{x}−{y}−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{maybe}\:\mathrm{I}\:\mathrm{do}\:\mathrm{not}\:\mathrm{understand}\:\mathrm{what}\:\mathrm{to}\:\mathrm{do},\:\mathrm{but} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{3}\:\mathrm{equations}\:\mathrm{in}\:\mathrm{3}\:\mathrm{unknown},\:\mathrm{so}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{an}\:\mathrm{unique}\:\mathrm{solution} \\ $$$$\left(\mathrm{1}\right)\:\Rightarrow\:{y}=\frac{\mathrm{1}−{mx}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\Rightarrow\:{x}=\frac{{m}+\mathrm{6}}{{m}^{\mathrm{2}} −\mathrm{4}}\:\Rightarrow\:{y}=−\frac{\mathrm{3}{m}+\mathrm{2}}{{m}^{\mathrm{2}} −\mathrm{4}} \\ $$$$\left(\mathrm{3}\right)\:\Rightarrow\:{m}=\frac{\mathrm{10}}{\mathrm{3}}\:\Rightarrow\:{x}=\frac{\mathrm{21}}{\mathrm{16}}\wedge{y}=−\frac{\mathrm{27}}{\mathrm{16}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com