
Question Number 6302 by sanusihammed last updated on 22/Jun/16
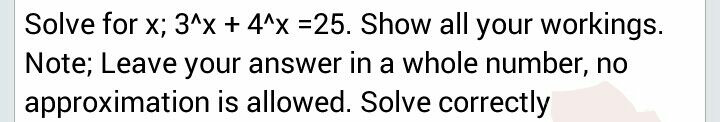
Commented by Rasheed Soomro last updated on 22/Jun/16
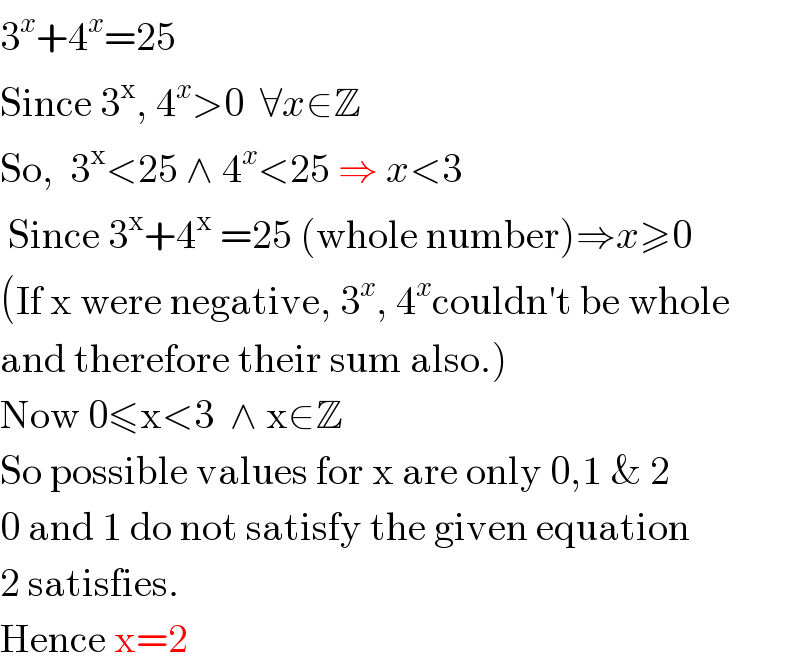
$$\mathrm{3}^{{x}} +\mathrm{4}^{{x}} =\mathrm{25} \\ $$$$\mathrm{Since}\:\mathrm{3}^{\mathrm{x}} ,\:\mathrm{4}^{{x}} >\mathrm{0}\:\:\forall{x}\in\mathbb{Z} \\ $$$$\mathrm{So},\:\:\mathrm{3}^{\mathrm{x}} <\mathrm{25}\:\wedge\:\mathrm{4}^{{x}} <\mathrm{25}\:\Rightarrow\:{x}<\mathrm{3} \\ $$$$\:\mathrm{Since}\:\mathrm{3}^{\mathrm{x}} +\mathrm{4}^{\mathrm{x}} \:=\mathrm{25}\:\left(\mathrm{whole}\:\mathrm{number}\right)\Rightarrow{x}\geqslant\mathrm{0}\:\:\:\:\: \\ $$$$\left(\mathrm{If}\:\mathrm{x}\:\mathrm{were}\:\mathrm{negative},\:\mathrm{3}^{{x}} ,\:\mathrm{4}^{{x}} \mathrm{couldn}'\mathrm{t}\:\mathrm{be}\:\mathrm{whole}\right. \\ $$$$\left.\mathrm{and}\:\mathrm{therefore}\:\mathrm{their}\:\mathrm{sum}\:\mathrm{also}.\right) \\ $$$$\mathrm{Now}\:\mathrm{0}\leqslant\mathrm{x}<\mathrm{3}\:\:\wedge\:\mathrm{x}\in\mathbb{Z} \\ $$$$\mathrm{So}\:\mathrm{possible}\:\mathrm{values}\:\mathrm{for}\:\mathrm{x}\:\mathrm{are}\:\mathrm{only}\:\mathrm{0},\mathrm{1}\:\&\:\mathrm{2} \\ $$$$\mathrm{0}\:\mathrm{and}\:\mathrm{1}\:\mathrm{do}\:\mathrm{not}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation} \\ $$$$\mathrm{2}\:\mathrm{satisfies}. \\ $$$$\mathrm{Hence}\:\mathrm{x}=\mathrm{2} \\ $$
Commented by Yozzii last updated on 22/Jun/16
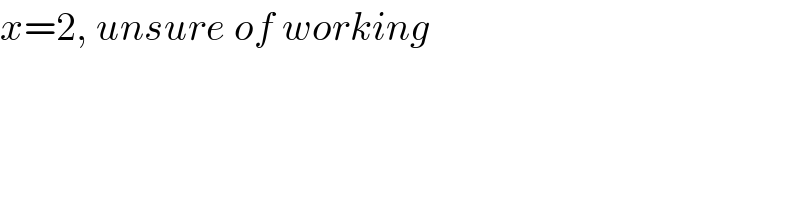
$${x}=\mathrm{2},\:{unsure}\:{of}\:{working} \\ $$
Commented by FilupSmith last updated on 23/Jun/16
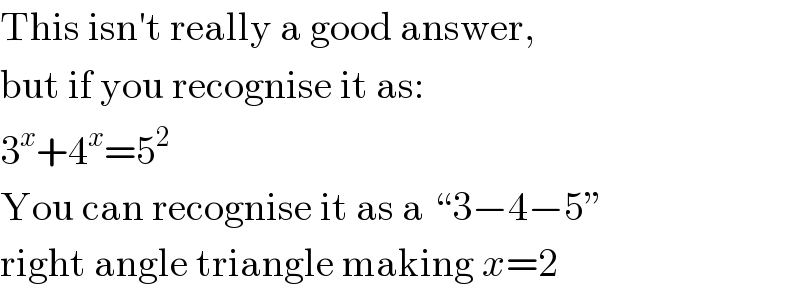
$$\mathrm{This}\:\mathrm{isn}'\mathrm{t}\:\mathrm{really}\:\mathrm{a}\:\mathrm{good}\:\mathrm{answer}, \\ $$$$\mathrm{but}\:\mathrm{if}\:\mathrm{you}\:\mathrm{recognise}\:\mathrm{it}\:\mathrm{as}: \\ $$$$\mathrm{3}^{{x}} +\mathrm{4}^{{x}} =\mathrm{5}^{\mathrm{2}} \\ $$$$\mathrm{You}\:\mathrm{can}\:\mathrm{recognise}\:\mathrm{it}\:\mathrm{as}\:\mathrm{a}\:``\mathrm{3}−\mathrm{4}−\mathrm{5}'' \\ $$$$\mathrm{right}\:\mathrm{angle}\:\mathrm{triangle}\:\mathrm{making}\:{x}=\mathrm{2} \\ $$
