
Question Number 62826 by Cheyboy last updated on 25/Jun/19

Commented by mathmax by abdo last updated on 25/Jun/19
![b) I =∫_0 ^π ((sinθ)/(√(π−θ))) changement(√(π−θ)) =x give I =∫_(√π) ^0 ((sin(π−x^2 ))/x) (−2x)dx = 2 ∫_0 ^(√π) sin(x^2 )dx the function x→sin(x^2 ) is continous on[0,(√π)] so the integral converges. 4b) i think the Q .here is find lim_(n→∞) (1/n){ f((1/n))+f((2/n))+....f((n/n))} =lim_(n→+∞) ((1−o)/n) Σ_(k=0) ^n f(0 +((k(1−o))/n)) =∫_0 ^1 f(x)dx .](Q62829.png)
$$\left.{b}\right)\:{I}\:=\int_{\mathrm{0}} ^{\pi} \:\:\frac{{sin}\theta}{\sqrt{\pi−\theta}}\:\:{changement}\sqrt{\pi−\theta}\:={x}\:{give}\:{I}\:=\int_{\sqrt{\pi}} ^{\mathrm{0}} \:\frac{{sin}\left(\pi−{x}^{\mathrm{2}} \right)}{{x}}\:\left(−\mathrm{2}{x}\right){dx} \\ $$$$=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\sqrt{\pi}} \:\:{sin}\left({x}^{\mathrm{2}} \right){dx}\:\:\:\:{the}\:{function}\:{x}\rightarrow{sin}\left({x}^{\mathrm{2}} \right)\:{is}\:{continous}\:{on}\left[\mathrm{0},\sqrt{\pi}\right]\:{so}\:{the}\: \\ $$$${integral}\:\:{converges}. \\ $$$$\left.\mathrm{4}{b}\right)\:\:{i}\:{think}\:{the}\:{Q}\:.{here}\:{is}\:{find}\:{lim}_{{n}\rightarrow\infty} \:\frac{\mathrm{1}}{{n}}\left\{\:{f}\left(\frac{\mathrm{1}}{{n}}\right)+{f}\left(\frac{\mathrm{2}}{{n}}\right)+....{f}\left(\frac{{n}}{{n}}\right)\right\} \\ $$$$={lim}_{{n}\rightarrow+\infty} \:\frac{\mathrm{1}−{o}}{{n}}\:\sum_{{k}=\mathrm{0}} ^{{n}} {f}\left(\mathrm{0}\:+\frac{{k}\left(\mathrm{1}−{o}\right)}{{n}}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\:. \\ $$
Commented by mathmax by abdo last updated on 25/Jun/19
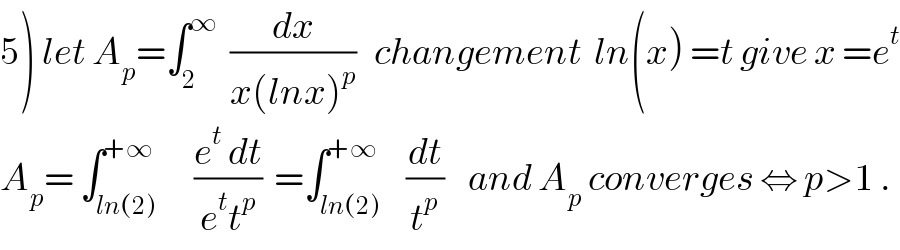
$$\left.\mathrm{5}\right)\:{let}\:{A}_{{p}} =\int_{\mathrm{2}} ^{\infty} \:\:\frac{{dx}}{{x}\left({lnx}\right)^{{p}} }\:\:\:{changement}\:\:{ln}\left({x}\right)\:={t}\:{give}\:{x}\:={e}^{{t}} \\ $$$${A}_{{p}} =\:\int_{{ln}\left(\mathrm{2}\right)} ^{+\infty} \:\:\:\:\:\frac{{e}^{{t}} \:{dt}}{{e}^{{t}} {t}^{{p}} }\:\:=\int_{{ln}\left(\mathrm{2}\right)} ^{+\infty} \:\:\:\frac{{dt}}{{t}^{{p}} }\:\:\:\:{and}\:{A}_{{p}} \:{converges}\:\Leftrightarrow\:{p}>\mathrm{1}\:. \\ $$
Commented by Cheyboy last updated on 26/Jun/19

$${Godbless}\:{you}\:{Sir} \\ $$
Commented by mathmax by abdo last updated on 26/Jun/19
$${you}\:{are}\:{welcome}\:{sir}. \\ $$
