
Question Number 62790 by Tawa1 last updated on 25/Jun/19
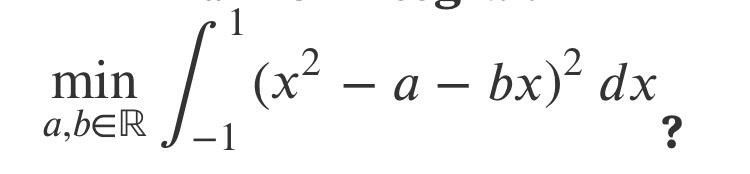
Commented by Tawa1 last updated on 25/Jun/19
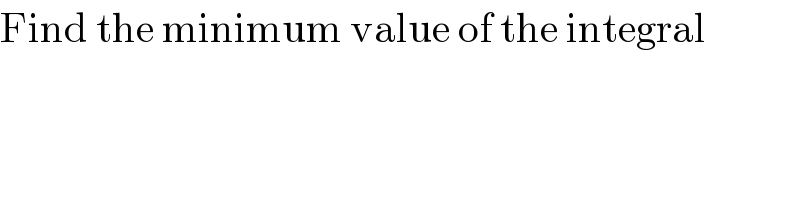
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{integral} \\ $$
Answered by MJS last updated on 25/Jun/19
![∫_(−1) ^1 (x^2 −bx−a)^2 dx=∫_(−1) ^1 (x^4 −2bx^3 −(2a−b^2 )x^2 +2abx+a^2 )dx= =[(1/5)x^5 −(b/2)x^4 −((2a−b^2 )/3)x^3 +abx^2 +a^2 x]_(−1) ^1 = =2a^2 −(4/3)a+(2/3)b^2 +(2/5) min (2a^2 −(4/3)a+(2/3)b^2 +(2/5)) = =(2/5)+min (2a^2 −(4/3)a) +min ((2/3)b^2 ) = =(2/5)+min (2a^2 −(4/3)a) +0 (d/da)[2a^2 −(4/3)a]=4a−(4/3)=0 ⇒ a=(1/3) ⇒ min (∫_(−1) ^1 (x^2 −bx−a)^2 dx)=(8/(45))](Q62792.png)
$$\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\left({x}^{\mathrm{2}} −{bx}−{a}\right)^{\mathrm{2}} {dx}=\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\left({x}^{\mathrm{4}} −\mathrm{2}{bx}^{\mathrm{3}} −\left(\mathrm{2}{a}−{b}^{\mathrm{2}} \right){x}^{\mathrm{2}} +\mathrm{2}{abx}+{a}^{\mathrm{2}} \right){dx}= \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{5}}{x}^{\mathrm{5}} −\frac{{b}}{\mathrm{2}}{x}^{\mathrm{4}} −\frac{\mathrm{2}{a}−{b}^{\mathrm{2}} }{\mathrm{3}}{x}^{\mathrm{3}} +{abx}^{\mathrm{2}} +{a}^{\mathrm{2}} {x}\right]_{−\mathrm{1}} ^{\mathrm{1}} = \\ $$$$=\mathrm{2}{a}^{\mathrm{2}} −\frac{\mathrm{4}}{\mathrm{3}}{a}+\frac{\mathrm{2}}{\mathrm{3}}{b}^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{5}} \\ $$$$\mathrm{min}\:\left(\mathrm{2}{a}^{\mathrm{2}} −\frac{\mathrm{4}}{\mathrm{3}}{a}+\frac{\mathrm{2}}{\mathrm{3}}{b}^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{5}}\right)\:= \\ $$$$=\frac{\mathrm{2}}{\mathrm{5}}+\mathrm{min}\:\left(\mathrm{2}{a}^{\mathrm{2}} −\frac{\mathrm{4}}{\mathrm{3}}{a}\right)\:+\mathrm{min}\:\left(\frac{\mathrm{2}}{\mathrm{3}}{b}^{\mathrm{2}} \right)\:= \\ $$$$=\frac{\mathrm{2}}{\mathrm{5}}+\mathrm{min}\:\left(\mathrm{2}{a}^{\mathrm{2}} −\frac{\mathrm{4}}{\mathrm{3}}{a}\right)\:+\mathrm{0} \\ $$$$\frac{{d}}{{da}}\left[\mathrm{2}{a}^{\mathrm{2}} −\frac{\mathrm{4}}{\mathrm{3}}{a}\right]=\mathrm{4}{a}−\frac{\mathrm{4}}{\mathrm{3}}=\mathrm{0}\:\Rightarrow\:{a}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{min}\:\left(\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\left({x}^{\mathrm{2}} −{bx}−{a}\right)^{\mathrm{2}} {dx}\right)=\frac{\mathrm{8}}{\mathrm{45}} \\ $$
Commented by Prithwish sen last updated on 25/Jun/19

$$\mathrm{Sir}\:\mathrm{great}\:! \\ $$
Commented by Tawa1 last updated on 25/Jun/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
