
Question Number 62542 by mr W last updated on 22/Jun/19
Commented by mr W last updated on 22/Jun/19

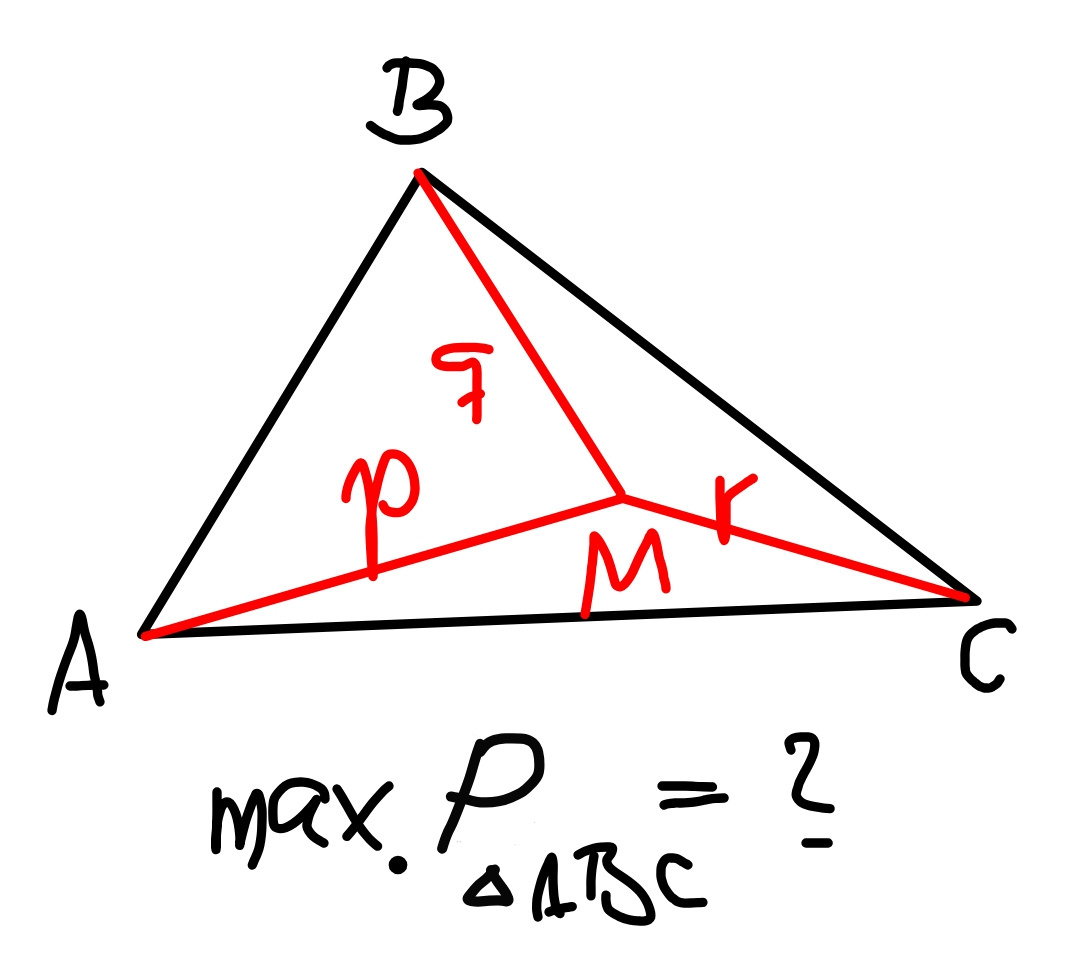
$${the}\:{distances}\:{of}\:{a}\:{point}\:{M}\:{to}\:{the} \\ $$$${vertexes}\:{of}\:{a}\:{triangle}\:{are}\:{p},{q},{r}. \\ $$$${find}\:{the}\:{side}\:{lengthes}\:{and}\:{hence}\:{the} \\ $$$${perimeter}\:{of}\:{the}\:{triangle}\:{with}\:{the} \\ $$$${largest}\:{perimeter}. \\ $$
Answered by mr W last updated on 23/Jun/19
![i think M should be center of incircle such that perimeter is maximum. let k=radius of incircle ∠A=2 sin^(−1) (k/p) ∠B=2 sin^(−1) (k/q) ∠C=2 sin^(−1) (k/r) ∠A+∠B+∠C=π ⇒sin^(−1) (k/p)+sin^(−1) (k/q)+sin^(−1) (k/r)=(π/2) ⇒cos (sin^(−1) (k/p)+sin^(−1) (k/q))=cos ((π/2)−sin^(−1) (k/r)) (√((1−(k^2 /p^2 ))(1−(k^2 /q^2 ))))−(k^2 /(pq))=(k/r) (√((1−(k^2 /p^2 ))(1−(k^2 /q^2 ))))=(k/r)+(k^2 /(pq)) (1−(k^2 /p^2 ))(1−(k^2 /q^2 ))=(k^2 /r^2 )+(k^4 /(p^2 q^2 ))+((2k^3 )/(pqr)) ((2k^3 )/(pqr))+((1/p^2 )+(1/q^2 )+(1/r^2 ))k^2 −1=0 k^3 +3((p^2 q^2 +q^2 r^2 +r^2 p^2 )/(6pqr))k^2 −2((pqr)/4)=0 ⇒k^3 +3uk^2 −2v=0 k=s−u ⇒s^3 −3u^2 s+2(u^3 −v)=0 s=2u sin {(1/3) sin^(−1) (1−(v/u^3 ))+((2nπ)/3)} k=u[2 sin {(1/3) sin^(−1) (1−(v/u^3 ))+((2π)/3)}−1]>0 ⇒k=((p^2 q^2 +q^2 r^2 +r^2 p^2 )/(6pqr))[2 sin {(1/3) sin^(−1) (1−((54p^4 q^4 r^4 )/((p^2 q^2 +q^2 r^2 +r^2 p^2 )^3 )))+((2π)/3)}−1] ⇒a=(√(q^2 −k^2 ))+(√(r^2 −k^2 )) ⇒b=(√(r^2 −k^2 ))+(√(p^2 −k^2 )) ⇒c=(√(p^2 −k^2 ))+(√(q^2 −k^2 ))](Q62558.png)
$${i}\:{think}\:{M}\:{should}\:{be}\:{center}\:{of}\:{incircle} \\ $$$${such}\:{that}\:{perimeter}\:{is}\:{maximum}. \\ $$$${let}\:{k}={radius}\:{of}\:{incircle} \\ $$$$\angle{A}=\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{{k}}{{p}} \\ $$$$\angle{B}=\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{{k}}{{q}} \\ $$$$\angle{C}=\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{{k}}{{r}} \\ $$$$\angle{A}+\angle{B}+\angle{C}=\pi \\ $$$$\Rightarrow\mathrm{sin}^{−\mathrm{1}} \frac{{k}}{{p}}+\mathrm{sin}^{−\mathrm{1}} \frac{{k}}{{q}}+\mathrm{sin}^{−\mathrm{1}} \frac{{k}}{{r}}=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{cos}\:\left(\mathrm{sin}^{−\mathrm{1}} \frac{{k}}{{p}}+\mathrm{sin}^{−\mathrm{1}} \frac{{k}}{{q}}\right)=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−\mathrm{sin}^{−\mathrm{1}} \frac{{k}}{{r}}\right) \\ $$$$\sqrt{\left(\mathrm{1}−\frac{{k}^{\mathrm{2}} }{{p}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{k}^{\mathrm{2}} }{{q}^{\mathrm{2}} }\right)}−\frac{{k}^{\mathrm{2}} }{{pq}}=\frac{{k}}{{r}} \\ $$$$\sqrt{\left(\mathrm{1}−\frac{{k}^{\mathrm{2}} }{{p}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{k}^{\mathrm{2}} }{{q}^{\mathrm{2}} }\right)}=\frac{{k}}{{r}}+\frac{{k}^{\mathrm{2}} }{{pq}} \\ $$$$\left(\mathrm{1}−\frac{{k}^{\mathrm{2}} }{{p}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{k}^{\mathrm{2}} }{{q}^{\mathrm{2}} }\right)=\frac{{k}^{\mathrm{2}} }{{r}^{\mathrm{2}} }+\frac{{k}^{\mathrm{4}} }{{p}^{\mathrm{2}} {q}^{\mathrm{2}} }+\frac{\mathrm{2}{k}^{\mathrm{3}} }{{pqr}} \\ $$$$\frac{\mathrm{2}{k}^{\mathrm{3}} }{{pqr}}+\left(\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\frac{\mathrm{1}}{{q}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }\right){k}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$${k}^{\mathrm{3}} +\mathrm{3}\frac{{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} }{\mathrm{6}{pqr}}{k}^{\mathrm{2}} −\mathrm{2}\frac{{pqr}}{\mathrm{4}}=\mathrm{0} \\ $$$$\Rightarrow{k}^{\mathrm{3}} +\mathrm{3}{uk}^{\mathrm{2}} −\mathrm{2}{v}=\mathrm{0} \\ $$$${k}={s}−{u} \\ $$$$\Rightarrow{s}^{\mathrm{3}} −\mathrm{3}{u}^{\mathrm{2}} {s}+\mathrm{2}\left({u}^{\mathrm{3}} −{v}\right)=\mathrm{0} \\ $$$${s}=\mathrm{2}{u}\:\mathrm{sin}\:\left\{\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−\frac{{v}}{{u}^{\mathrm{3}} }\right)+\frac{\mathrm{2}{n}\pi}{\mathrm{3}}\right\} \\ $$$${k}={u}\left[\mathrm{2}\:\mathrm{sin}\:\left\{\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−\frac{{v}}{{u}^{\mathrm{3}} }\right)+\frac{\mathrm{2}\pi}{\mathrm{3}}\right\}−\mathrm{1}\right]>\mathrm{0} \\ $$$$\Rightarrow{k}=\frac{{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} }{\mathrm{6}{pqr}}\left[\mathrm{2}\:\mathrm{sin}\:\left\{\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{54}{p}^{\mathrm{4}} {q}^{\mathrm{4}} {r}^{\mathrm{4}} }{\left({p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} \right)^{\mathrm{3}} }\right)+\frac{\mathrm{2}\pi}{\mathrm{3}}\right\}−\mathrm{1}\right] \\ $$$$\Rightarrow{a}=\sqrt{{q}^{\mathrm{2}} −{k}^{\mathrm{2}} }+\sqrt{{r}^{\mathrm{2}} −{k}^{\mathrm{2}} } \\ $$$$\Rightarrow{b}=\sqrt{{r}^{\mathrm{2}} −{k}^{\mathrm{2}} }+\sqrt{{p}^{\mathrm{2}} −{k}^{\mathrm{2}} } \\ $$$$\Rightarrow{c}=\sqrt{{p}^{\mathrm{2}} −{k}^{\mathrm{2}} }+\sqrt{{q}^{\mathrm{2}} −{k}^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 22/Jun/19
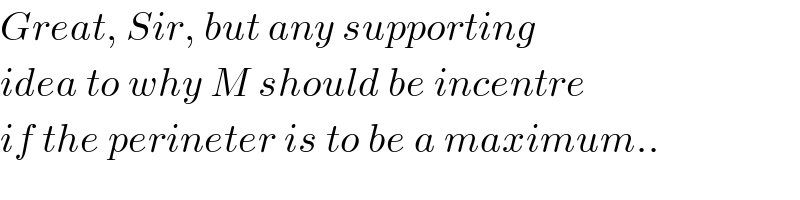
$${Great},\:{Sir},\:{but}\:{any}\:{supporting} \\ $$$${idea}\:{to}\:{why}\:{M}\:{should}\:{be}\:{incentre} \\ $$$${if}\:{the}\:{perineter}\:{is}\:{to}\:{be}\:{a}\:{maximum}.. \\ $$
Commented by mr W last updated on 23/Jun/19
Commented by mr W last updated on 23/Jun/19

$$\left({see}\:{diagram}\:{above}\right) \\ $$$${let}'{s}\:{look}\:{at}\:{the}\:{case}\:{when}\:{B},\:{C}\:{are} \\ $$$${given}\:{and}\:{A}\:{is}\:{to}\:{determine},\:{which} \\ $$$${must}\:{lie}\:{on}\:{a}\:{circle}\:{with}\:{center}\:{M}. \\ $$$${the}\:{law}\:{of}\:{nature}\:{tells}\:{us}:\:{when}\:{the} \\ $$$${path}\:{from}\:{B}\:{to}\:{C}\:{via}\:{A}\:{should}\:{be}\: \\ $$$${optimum}\:\left({minimum}\:{or}\:{maximum}\right), \\ $$$${it}\:{must}\:{follow}\:{the}\:{path}\:{of}\:{a}\:{light}\:{ray}, \\ $$$${i}.{e}.\:{as}\:{if}\:{the}\:{circle}\:{were}\:{a}\:{mirror}.\: \\ $$$${point}\:{A}\:{should}\:{be}\:{the}\:{reflection}\:{point} \\ $$$${of}\:{the}\:{light}\:{ray}\:{and}\:{therefore}\:{AM} \\ $$$${is}\:{the}\:{bisector}\:{of}\:{angle}\:\angle{BAC}. \\ $$$${when}\:{we}\:{consider}\:{not}\:{only}\:{point}\:{A}, \\ $$$${but}\:{also}\:{other}\:{vertexes},\:{we}\:{will} \\ $$$${conclude}\:{that}\:{the}\:{triangle}\:{has}\:{optimum} \\ $$$${perimeter}\:{when}\:{M}\:{is}\:{on}\:{the}\:{bisectors} \\ $$$${of}\:{all}\:{angles}\:{of}\:{the}\:{triangle},\:{that} \\ $$$${means}\:{M}\:{is}\:{the}\:{center}\:{of}\:{its}\:{incircle}. \\ $$
Commented by mr W last updated on 23/Jun/19

Commented by mr W last updated on 23/Jun/19

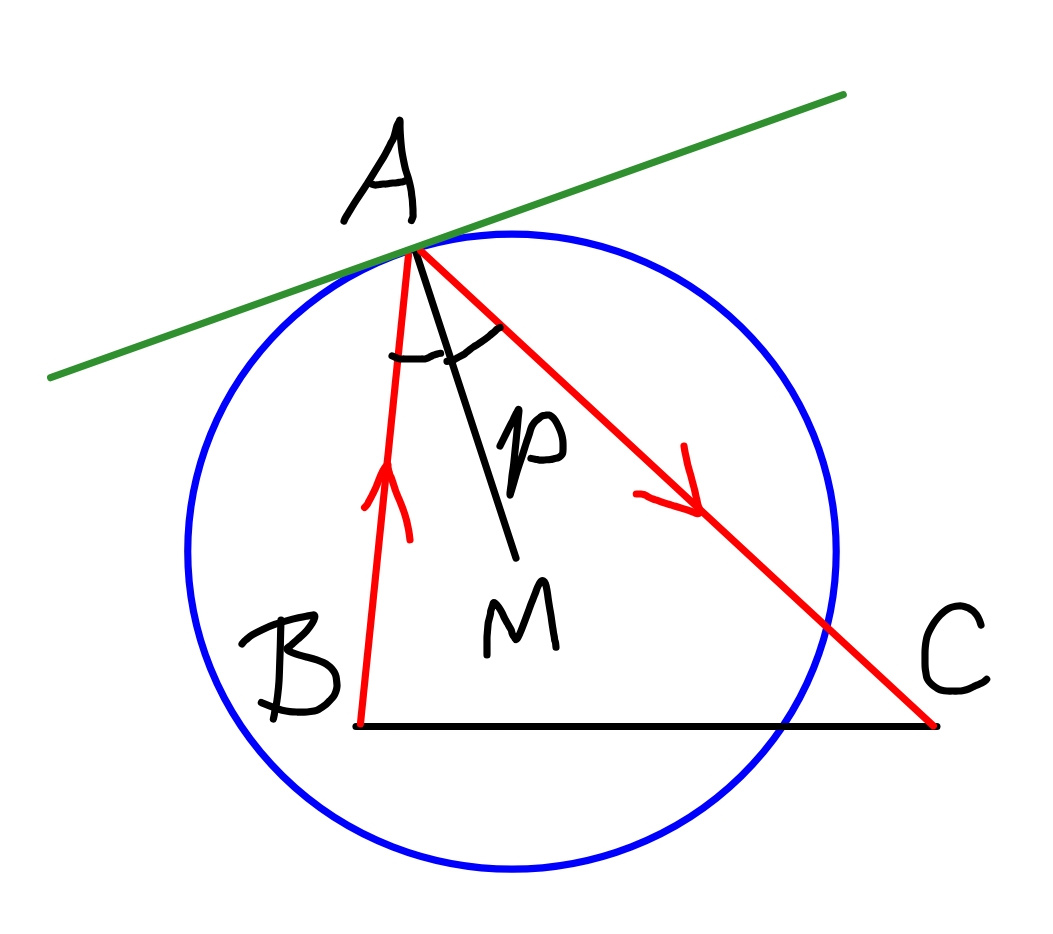
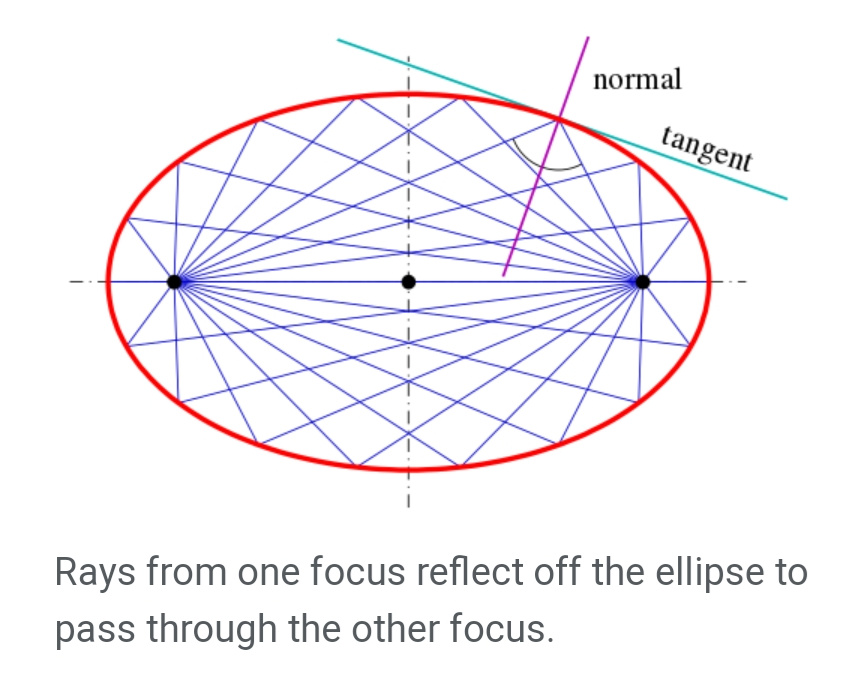
$$\left({see}\:{diagram}\:{above}\right) \\ $$$${we}\:{can}\:{also}\:{consider}\:{like}\:{this}: \\ $$$${point}\:{A}\:{lies}\:{on}\:{circle}\:{with}\:{center}\:{M}. \\ $$$${we}\:{know}\:{the}\:{locus}\:{of}\:{a}\:{point},\:{whose} \\ $$$${sum}\:{of}\:{distances}\:{to}\:{B}\:{and}\:{C}\:{is} \\ $$$${constant},\:{is}\:{an}\:{ellipse}\:{with}\:{focuses} \\ $$$${at}\:{point}\:{B}\:{and}\:{C}.\:\:{infinite}\:{such} \\ $$$${ellipses}\:{are}\:{possible}.\:{the}\:{sum}\:{of}\:{the} \\ $$$${distances}\:{AB}+{AC}\:{is}\:{maximum}, \\ $$$${when}\:{A}\:{also}\:{lies}\:{on}\:{such}\:{an}\:{ellipse} \\ $$$${which}\:{touches}\:{the}\:{circle}\:{with}\:{center}\:{M}. \\ $$$${in}\:{this}\:{case}\:{AM}\:{is}\:{also}\:{a}\:{normal} \\ $$$${of}\:{the}\:{ellipse}.\:{we}\:{know}\:{a}\:{light}\:{ray}\: \\ $$$${from}\:{a}\:{focus}\:{of}\:{an}\:{ellipse}\:{passes}\:{also} \\ $$$${through}\:{the}\:{other}\:{focus}\:{after}\:{reflection} \\ $$$${on}\:{the}\:{ellipse},\:{i}.{e}.\:{the}\:{normal}\:{at} \\ $$$${point}\:{A}\:{is}\:{the}\:{angle}\:{bisector}\:{of}\:{the} \\ $$$${light}\:{ray}\:{BA}\:{and}\:{AC},\:{see}\:{also} \\ $$$${following}\:{diagram}. \\ $$
Commented by mr W last updated on 23/Jun/19
Commented by mr W last updated on 23/Jun/19

$${due}\:{to}\:{this}\:{consideration}\:{i}\:{think}\:{the} \\ $$$${triangle}\:{we}\:{search}\:{is}\:{that}\:{one}\:{whose} \\ $$$${incircle}\:{center}\:{is}\:{the}\:{point}\:{M}. \\ $$$${we}\:{don}'{t}\:{need}\:{to}\:{apply}\:{calculus}\:{method} \\ $$$${like}\:\frac{\partial{P}}{\partial\theta}=\mathrm{0}\:{and}\:\frac{\partial{P}}{\partial\varphi}=\mathrm{0}. \\ $$
Commented by ajfour last updated on 23/Jun/19

$${Plentiful}\:{evidence},\:{Sir}.\:{Thanks} \\ $$$${a}\:{lot}.\:{But}\:{yet}\:{an}\:{analytical}\:{way} \\ $$$${to}\:{prove}\:{this}\:{isn}'{t}\:{easy}\:\left({i}\:{tried}\right)! \\ $$
