Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 62424 by aliesam last updated on 21/Jun/19

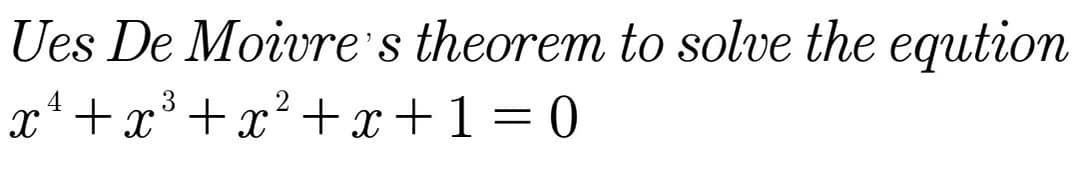
Commented by mathmax by abdo last updated on 21/Jun/19

1 is not root for this equatio (e) ⇔((1−x^5 )/(1−x)) =0 ⇔ x^5 =1 let x =re^(iθ) ( we take x from C) x^5 =1 ⇔ r^5 e^(5iθ) =e^(i2kπ) ⇔ r=1 and 5θ =2kπ ⇒θ =((2kπ)/5) k∈[0,4] the roots are x_k =e^(i((2kπ)/5)) x_0 is not roots ⇒k∈[1,4] x_1 =e^((i2π)/5) ,x_2 = e^(i(((4π)/5))) =e^(i(π−(π/5))) =−e^(−((iπ)/5)) x_3 = e^(i(((6π)/5))) =e^(i(π+(π/5))) =−e^((iπ)/5) x_4 =e^(i(((8π)/5))) =e^(i(2π−((2π)/5))) = e^(−((i2π)/5)) and we see that x_4 =x_1 ^− and x_3 =x_2 ^−

$$\mathrm{1}\:{is}\:{not}\:{root}\:{for}\:{this}\:{equatio}\: \\ $$$$\left({e}\right)\:\Leftrightarrow\frac{\mathrm{1}−{x}^{\mathrm{5}} }{\mathrm{1}−{x}}\:=\mathrm{0}\:\Leftrightarrow\:{x}^{\mathrm{5}} \:=\mathrm{1}\:\:{let}\:{x}\:={re}^{{i}\theta} \:\:\:\:\:\left(\:\:{we}\:{take}\:{x}\:{from}\:{C}\right) \\ $$$${x}^{\mathrm{5}} \:=\mathrm{1}\:\:\:\Leftrightarrow\:\:{r}^{\mathrm{5}} \:{e}^{\mathrm{5}{i}\theta} \:={e}^{{i}\mathrm{2}{k}\pi} \:\Leftrightarrow\:{r}=\mathrm{1}\:\:{and}\:\:\mathrm{5}\theta\:=\mathrm{2}{k}\pi\:\Rightarrow\theta\:=\frac{\mathrm{2}{k}\pi}{\mathrm{5}}\:\:\:\:{k}\in\left[\mathrm{0},\mathrm{4}\right] \\ $$$$\:{the}\:{roots}\:{are}\:{x}_{{k}} ={e}^{{i}\frac{\mathrm{2}{k}\pi}{\mathrm{5}}} \:\:\:\:{x}_{\mathrm{0}} {is}\:{not}\:{roots}\:\Rightarrow{k}\in\left[\mathrm{1},\mathrm{4}\right] \\ $$$${x}_{\mathrm{1}} ={e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{5}}} \:\:,{x}_{\mathrm{2}} =\:{e}^{{i}\left(\frac{\mathrm{4}\pi}{\mathrm{5}}\right)} \:={e}^{{i}\left(\pi−\frac{\pi}{\mathrm{5}}\right)} \:=−{e}^{−\frac{{i}\pi}{\mathrm{5}}} \\ $$$${x}_{\mathrm{3}} =\:{e}^{{i}\left(\frac{\mathrm{6}\pi}{\mathrm{5}}\right)} \:={e}^{{i}\left(\pi+\frac{\pi}{\mathrm{5}}\right)} \:=−{e}^{\frac{{i}\pi}{\mathrm{5}}} \\ $$$${x}_{\mathrm{4}} ={e}^{{i}\left(\frac{\mathrm{8}\pi}{\mathrm{5}}\right)} \:={e}^{{i}\left(\mathrm{2}\pi−\frac{\mathrm{2}\pi}{\mathrm{5}}\right)} \:=\:{e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{5}}} \:\:{and}\:\:{we}\:{see}\:{that}\:{x}_{\mathrm{4}} =\overset{−} {{x}}_{\mathrm{1}} \:\:\:\:{and}\:{x}_{\mathrm{3}} =\overset{−} {{x}}_{\mathrm{2}} \\ $$

Commented by aliesam last updated on 21/Jun/19

well done sir thank you

$$\mathrm{well}\:\mathrm{done}\:\mathrm{sir}\:\mathrm{thank}\:\mathrm{you} \\ $$

Answered by tanmay last updated on 21/Jun/19

another way devide both side by x^2 x^2 +(1/x^2 )+x+(1/x)+1=0 x+(1/x)=a→x^2 +(1/x^2 )=a^2 −2 a^2 −2+a+1=0 a^2 +a−1=0 a=((−1±(√(1+4)))/2)=((−1±(√5))/2) x+(1/x)=a x^2 −ax+1=0 x=((a±(√(a^2 −4)))/2) x=(((((−1+(√5))/2))±(√(((5+1−2(√5))/4)−4)))/2) x=((((−1+(√5))/2)±(√((−10−2(√5))/4)))/2) x=((−1+(√5) ±i(√(10+2(√5))))/4)→(x_1 ,x_2 ) x=((((−1−(√5))/2)±(√(((5+1+2(√5))/4)−4)))/2) x=((−1−(√5) ±(√(2(√5) −10)))/4) x=((−1−(√5) ±i(√(10−2(√5))))/4)(x_3 ,x_4 )

$${another}\:{way} \\ $$$${devide}\:{both}\:{side}\:{by}\:{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+{x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}=\mathrm{0} \\ $$$${x}+\frac{\mathrm{1}}{{x}}={a}\rightarrow{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }={a}^{\mathrm{2}} −\mathrm{2} \\ $$$${a}^{\mathrm{2}} −\mathrm{2}+{a}+\mathrm{1}=\mathrm{0} \\ $$$${a}^{\mathrm{2}} +{a}−\mathrm{1}=\mathrm{0} \\ $$$${a}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}}}{\mathrm{2}}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${x}+\frac{\mathrm{1}}{{x}}={a} \\ $$$${x}^{\mathrm{2}} −{ax}+\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{{a}\pm\sqrt{{a}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}} \\ $$$${x}=\frac{\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\pm\sqrt{\frac{\mathrm{5}+\mathrm{1}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}−\mathrm{4}}}{\mathrm{2}} \\ $$$${x}=\frac{\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\pm\sqrt{\frac{−\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}}}{\mathrm{2}} \\ $$$${x}=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}\:\pm{i}\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}\rightarrow\left({x}_{\mathrm{1}} ,{x}_{\mathrm{2}} \right) \\ $$$$ \\ $$$${x}=\frac{\frac{−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{5}+\mathrm{1}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}−\mathrm{4}}}{\mathrm{2}} \\ $$$${x}=\frac{−\mathrm{1}−\sqrt{\mathrm{5}}\:\pm\sqrt{\mathrm{2}\sqrt{\mathrm{5}}\:−\mathrm{10}}}{\mathrm{4}} \\ $$$${x}=\frac{−\mathrm{1}−\sqrt{\mathrm{5}}\:\pm{i}\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}\left({x}_{\mathrm{3}} ,{x}_{\mathrm{4}} \right) \\ $$$$ \\ $$

Commented by Tawa1 last updated on 21/Jun/19

Commented by Tawa1 last updated on 21/Jun/19

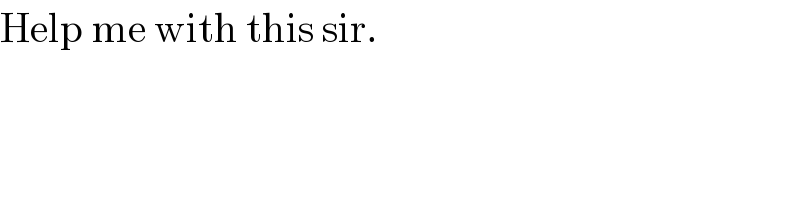
Help me with this sir.

$$\mathrm{Help}\:\mathrm{me}\:\mathrm{with}\:\mathrm{this}\:\mathrm{sir}.\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com