Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 62363 by Tawa1 last updated on 20/Jun/19

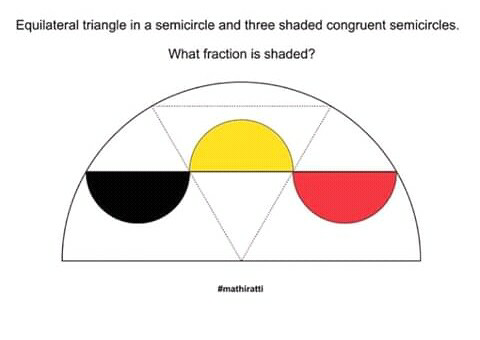
Answered by MJS last updated on 20/Jun/19

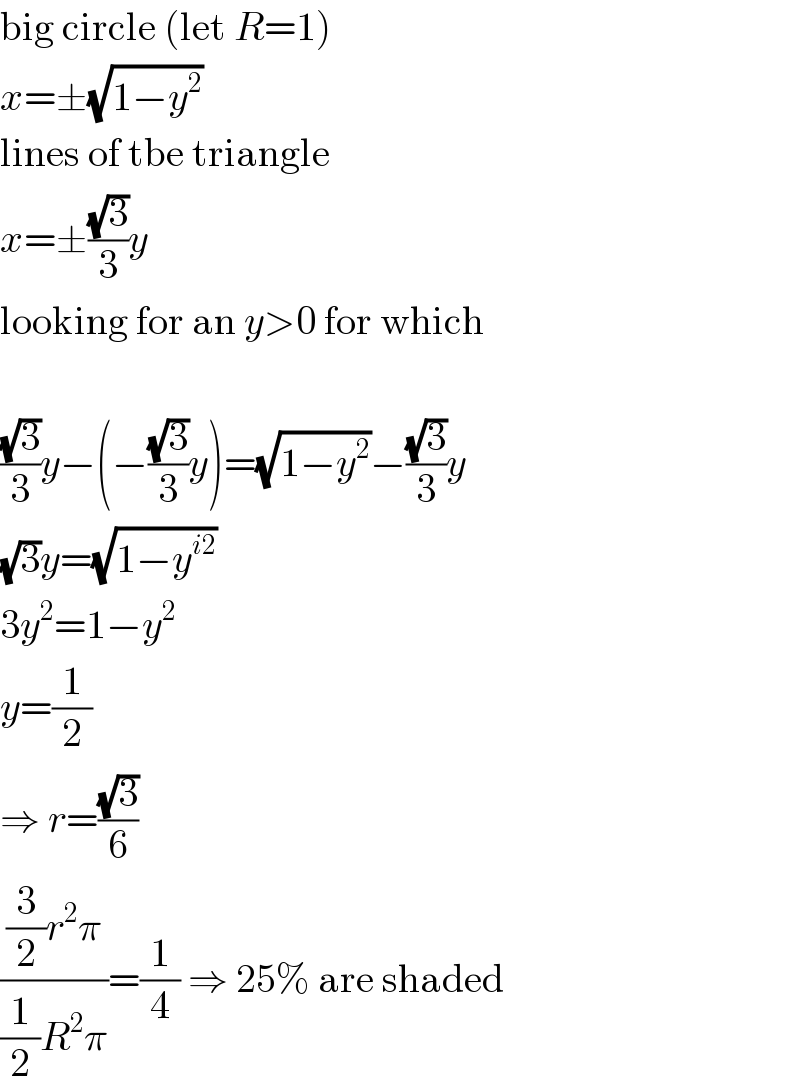
big circle (let R=1) x=±(√(1−y^2 )) lines of tbe triangle x=±((√3)/3)y looking for an y>0 for which ((√3)/3)y−(−((√3)/3)y)=(√(1−y^2 ))−((√3)/3)y (√3)y=(√(1−y^(i2) )) 3y^2 =1−y^2 y=(1/2) ⇒ r=((√3)/6) (((3/2)r^2 π)/((1/2)R^2 π))=(1/4) ⇒ 25% are shaded

$$\mathrm{big}\:\mathrm{circle}\:\left(\mathrm{let}\:{R}=\mathrm{1}\right) \\ $$$${x}=\pm\sqrt{\mathrm{1}−{y}^{\mathrm{2}} } \\ $$$$\mathrm{lines}\:\mathrm{of}\:\mathrm{tbe}\:\mathrm{triangle} \\ $$$${x}=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}{y} \\ $$$$\mathrm{looking}\:\mathrm{for}\:\mathrm{an}\:{y}>\mathrm{0}\:\mathrm{for}\:\mathrm{which} \\ $$$$ \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}{y}−\left(−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}{y}\right)=\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}{y} \\ $$$$\sqrt{\mathrm{3}}{y}=\sqrt{\mathrm{1}−{y}^{{i}\mathrm{2}} } \\ $$$$\mathrm{3}{y}^{\mathrm{2}} =\mathrm{1}−{y}^{\mathrm{2}} \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:{r}=\frac{\sqrt{\mathrm{3}}}{\mathrm{6}} \\ $$$$\frac{\frac{\mathrm{3}}{\mathrm{2}}{r}^{\mathrm{2}} \pi}{\frac{\mathrm{1}}{\mathrm{2}}{R}^{\mathrm{2}} \pi}=\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\:\mathrm{25\%}\:\mathrm{are}\:\mathrm{shaded} \\ $$

Commented by Tawa1 last updated on 20/Jun/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 20/Jun/19

R=radius of big semicircle r=radius small semicircles R^2 =(3r)^2 +((√3)r)^2 ⇒R^2 =12r^2 A_(shade) =3×((πr^2 )/2)=((3πr^2 )/2) A_(total) =((πR^2 )/2) ⇒(A_(shade) /A_(total) )=((3r^2 )/R^2 )=((3r^2 )/(12r^2 ))=(1/4)

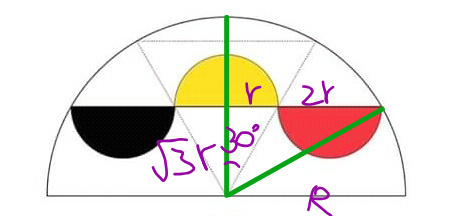
$${R}={radius}\:{of}\:{big}\:{semicircle} \\ $$$${r}={radius}\:{small}\:{semicircles} \\ $$$${R}^{\mathrm{2}} =\left(\mathrm{3}{r}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{R}^{\mathrm{2}} =\mathrm{12}{r}^{\mathrm{2}} \\ $$$${A}_{{shade}} =\mathrm{3}×\frac{\pi{r}^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{3}\pi{r}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${A}_{{total}} =\frac{\pi{R}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow\frac{{A}_{{shade}} }{{A}_{{total}} }=\frac{\mathrm{3}{r}^{\mathrm{2}} }{{R}^{\mathrm{2}} }=\frac{\mathrm{3}{r}^{\mathrm{2}} }{\mathrm{12}{r}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}} \\ $$

Commented by mr W last updated on 20/Jun/19

Commented by Tawa1 last updated on 20/Jun/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by Tawa1 last updated on 20/Jun/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com