
Question Number 59777 by Kunal12588 last updated on 14/May/19
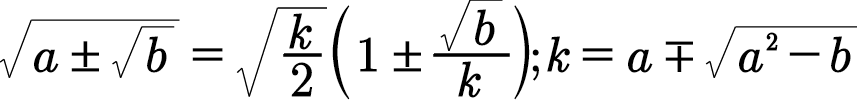
Commented by Kunal12588 last updated on 14/May/19
![I made aformula you can use it like this (√(2+(√3))) 1. find k k=a−(√(a^2 −b)) [(√(2+(√3)))] ⇒k=2−(√(4−3))=1 2. (√(2+(√3)))=(√(1/2))(1+((√3)/1))=((1+(√3))/(√2)) Can Anyone please try my formula](Q59778.png)
$${I}\:{made}\:{aformula}\:{you}\:{can}\:{use}\:{it}\:{like}\:{this} \\ $$$$\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$$\mathrm{1}.\:{find}\:{k} \\ $$$${k}={a}−\sqrt{{a}^{\mathrm{2}} −{b}}\:\:\:\:\left[\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\right] \\ $$$$\Rightarrow{k}=\mathrm{2}−\sqrt{\mathrm{4}−\mathrm{3}}=\mathrm{1} \\ $$$$\mathrm{2}.\:\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}\left(\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{1}}\right)=\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\sqrt{\mathrm{2}}} \\ $$$${Can}\:{Anyone}\:{please}\:{try}\:{my}\:{formula} \\ $$
Commented by Kunal12588 last updated on 14/May/19
![(√(2−(√3))) 1. find k k=a+(√(a^2 −b)) [(√(2−(√3)))] k=2+1=3 2. (√(2−(√3)))=(√(3/2))(1−((√3)/3))=(√(3/2))(1−(1/(√3)))=(((√3)−1)/(√2))](Q59779.png)
$$\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}} \\ $$$$\mathrm{1}.\:{find}\:{k} \\ $$$${k}={a}+\sqrt{{a}^{\mathrm{2}} −{b}}\:\:\:\:\:\left[\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\right] \\ $$$${k}=\mathrm{2}+\mathrm{1}=\mathrm{3} \\ $$$$\mathrm{2}.\:\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}=\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\left(\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\right)=\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\left(\mathrm{1}−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)=\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$
Commented by MJS last updated on 14/May/19

$$\mathrm{seems}\:\mathrm{to}\:\mathrm{work} \\ $$$$\mathrm{but}\:\mathrm{only}\:\mathrm{if}\:\sqrt{{a}^{\mathrm{2}} −{b}}\in\mathbb{N}\:\mathrm{otherwise}\:\mathrm{it}\:\mathrm{doesn}'\mathrm{t} \\ $$$$\mathrm{help} \\ $$
Commented by Kunal12588 last updated on 15/May/19

$${thank}\:{you}\:{sir} \\ $$
