
Question Number 59752 by Khairun Nisa last updated on 14/May/19
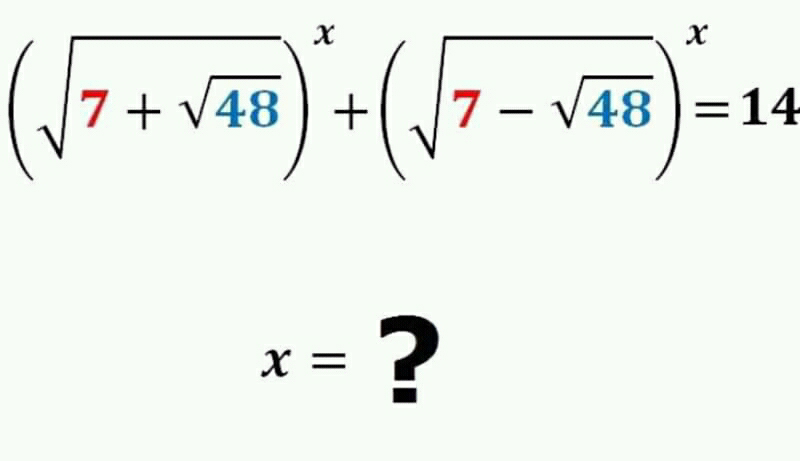
Commented by Smail last updated on 14/May/19
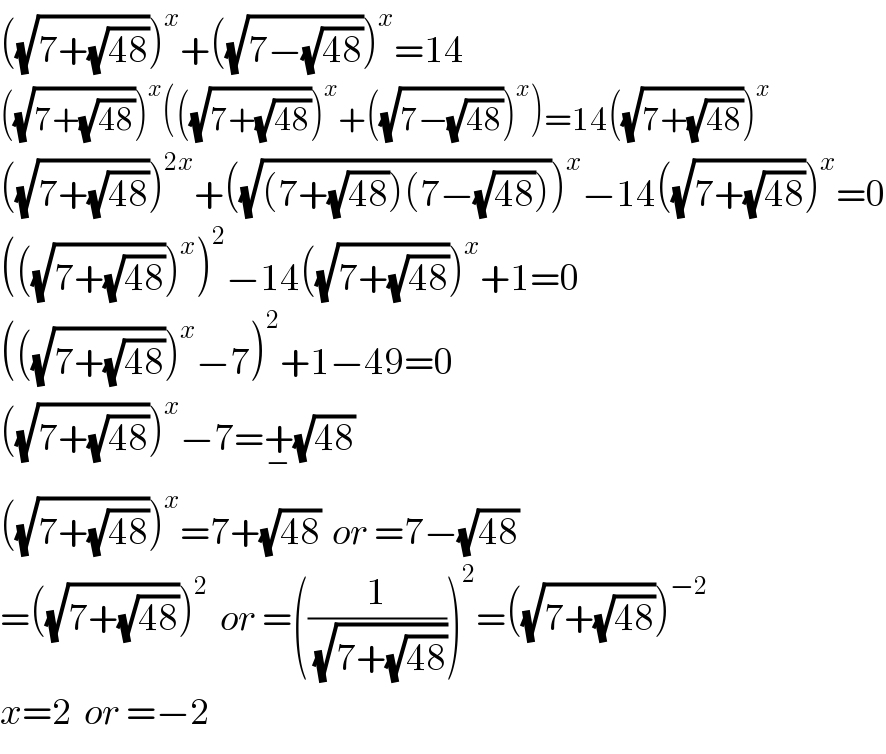
$$\left(\sqrt{\mathrm{7}+\sqrt{\mathrm{48}}}\right)^{{x}} +\left(\sqrt{\mathrm{7}−\sqrt{\mathrm{48}}}\right)^{{x}} =\mathrm{14} \\ $$$$\left(\sqrt{\mathrm{7}+\sqrt{\mathrm{48}}}\right)^{{x}} \left(\left(\sqrt{\mathrm{7}+\sqrt{\mathrm{48}}}\right)^{{x}} +\left(\sqrt{\mathrm{7}−\sqrt{\mathrm{48}}}\right)^{{x}} \right)=\mathrm{14}\left(\sqrt{\mathrm{7}+\sqrt{\mathrm{48}}}\right)^{{x}} \\ $$$$\left(\sqrt{\mathrm{7}+\sqrt{\mathrm{48}}}\right)^{\mathrm{2}{x}} +\left(\sqrt{\left(\mathrm{7}+\sqrt{\mathrm{48}}\right)\left(\mathrm{7}−\sqrt{\mathrm{48}}\right)}\right)^{{x}} −\mathrm{14}\left(\sqrt{\mathrm{7}+\sqrt{\mathrm{48}}}\right)^{{x}} =\mathrm{0} \\ $$$$\left(\left(\sqrt{\mathrm{7}+\sqrt{\mathrm{48}}}\right)^{{x}} \right)^{\mathrm{2}} −\mathrm{14}\left(\sqrt{\mathrm{7}+\sqrt{\mathrm{48}}}\right)^{{x}} +\mathrm{1}=\mathrm{0} \\ $$$$\left(\left(\sqrt{\mathrm{7}+\sqrt{\mathrm{48}}}\right)^{{x}} −\mathrm{7}\right)^{\mathrm{2}} +\mathrm{1}−\mathrm{49}=\mathrm{0} \\ $$$$\left(\sqrt{\mathrm{7}+\sqrt{\mathrm{48}}}\right)^{{x}} −\mathrm{7}=\underset{−} {+}\sqrt{\mathrm{48}} \\ $$$$\left(\sqrt{\mathrm{7}+\sqrt{\mathrm{48}}}\right)^{{x}} =\mathrm{7}+\sqrt{\mathrm{48}}\:\:{or}\:=\mathrm{7}−\sqrt{\mathrm{48}} \\ $$$$=\left(\sqrt{\mathrm{7}+\sqrt{\mathrm{48}}}\right)^{\mathrm{2}} \:\:{or}\:=\left(\frac{\mathrm{1}}{\sqrt{\mathrm{7}+\sqrt{\mathrm{48}}}}\right)^{\mathrm{2}} =\left(\sqrt{\mathrm{7}+\sqrt{\mathrm{48}}}\right)^{−\mathrm{2}} \\ $$$${x}=\mathrm{2}\:\:{or}\:=−\mathrm{2} \\ $$
Commented by Khairun Nisa last updated on 14/May/19
$${Thanku}\:{Sir} \\ $$
Answered by tanmay last updated on 14/May/19
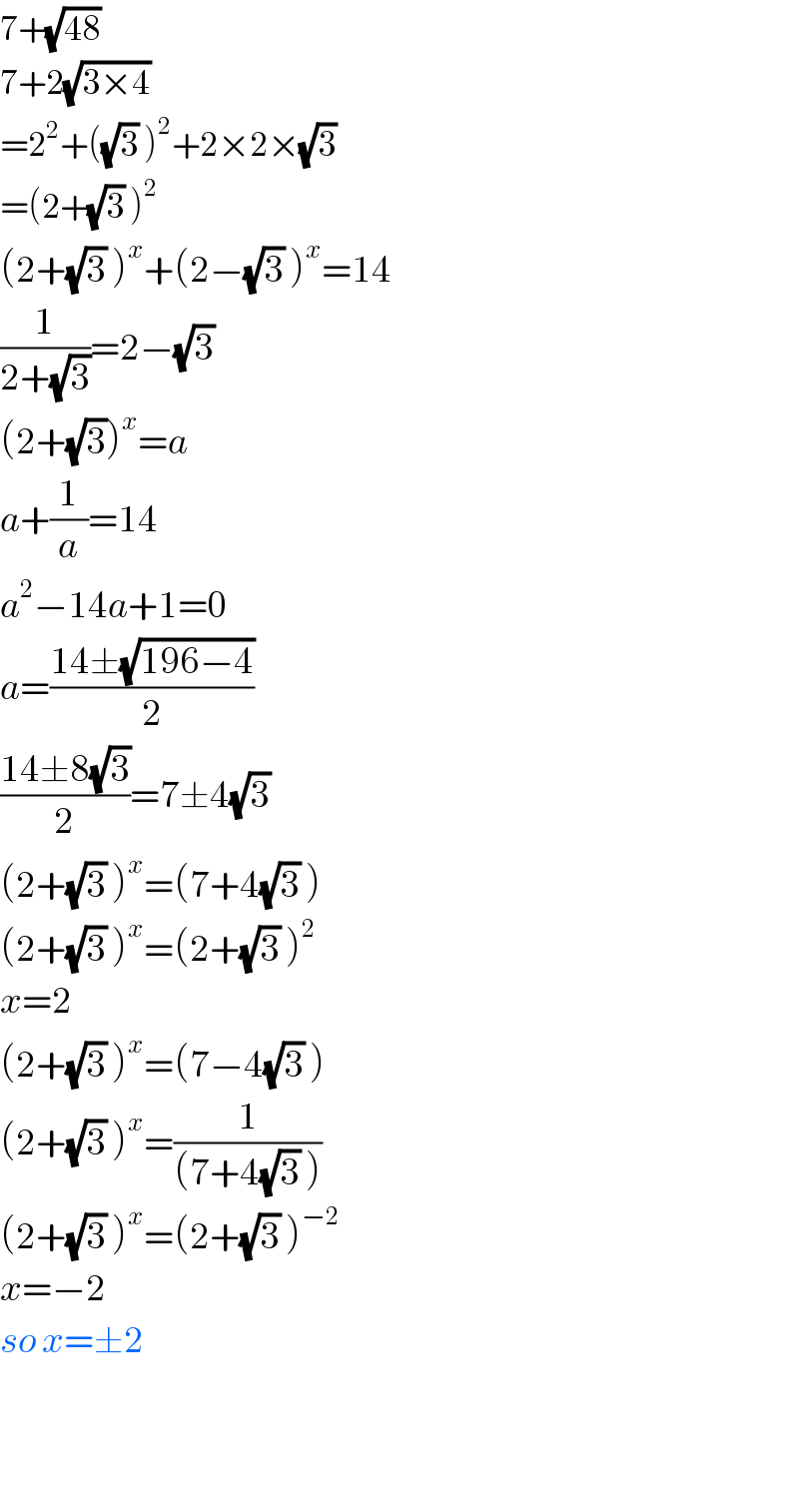
$$\mathrm{7}+\sqrt{\mathrm{48}}\: \\ $$$$\mathrm{7}+\mathrm{2}\sqrt{\mathrm{3}×\mathrm{4}}\: \\ $$$$=\mathrm{2}^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} +\mathrm{2}×\mathrm{2}×\sqrt{\mathrm{3}}\: \\ $$$$=\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{{x}} +\left(\mathrm{2}−\sqrt{\mathrm{3}}\:\right)^{{x}} =\mathrm{14} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{3}}}=\mathrm{2}−\sqrt{\mathrm{3}}\: \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{{x}} ={a} \\ $$$${a}+\frac{\mathrm{1}}{{a}}=\mathrm{14} \\ $$$${a}^{\mathrm{2}} −\mathrm{14}{a}+\mathrm{1}=\mathrm{0} \\ $$$${a}=\frac{\mathrm{14}\pm\sqrt{\mathrm{196}−\mathrm{4}}}{\mathrm{2}} \\ $$$$\frac{\mathrm{14}\pm\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{7}\pm\mathrm{4}\sqrt{\mathrm{3}}\: \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{{x}} =\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\:\right) \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{{x}} =\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} \\ $$$${x}=\mathrm{2} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{{x}} =\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\:\right) \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{{x}} =\frac{\mathrm{1}}{\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\:\right)} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{{x}} =\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{−\mathrm{2}} \\ $$$${x}=−\mathrm{2} \\ $$$${so}\:{x}=\pm\mathrm{2} \\ $$$$ \\ $$$$ \\ $$
Commented by Khairun Nisa last updated on 14/May/19
$${Thanku}\:{Sir} \\ $$
Commented by tanmay last updated on 14/May/19

$${most}\:{welcome} \\ $$
