
Question Number 59659 by aliesam last updated on 13/May/19
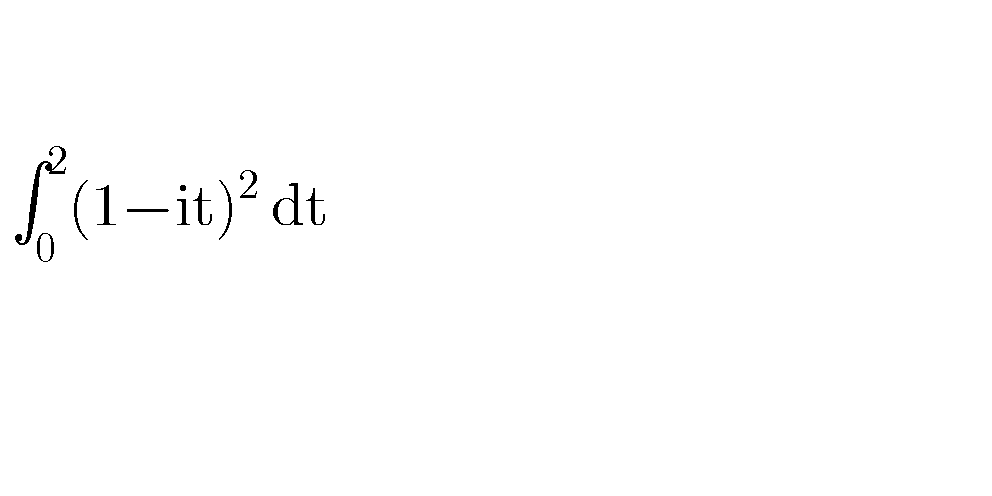
Commented by Mr X pcx last updated on 13/May/19

$${yes}\:{sir}. \\ $$
Commented by Mr X pcx last updated on 13/May/19
![I =∫_0 ^2 (1−2it −t^2 )dt =2−2i∫_0 ^2 tdt−∫_0 ^2 t^2 dt =2−2i[(t^2 /2)]_0 ^2 −[(t^3 /3)]_0 ^2 =2+2i(2)−(8/3) =−(2/3) +4i .](Q59710.png)
$${I}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{1}−\mathrm{2}{it}\:−{t}^{\mathrm{2}} \right){dt}\:=\mathrm{2}−\mathrm{2}{i}\int_{\mathrm{0}} ^{\mathrm{2}} {tdt}−\int_{\mathrm{0}} ^{\mathrm{2}} {t}^{\mathrm{2}} {dt} \\ $$$$=\mathrm{2}−\mathrm{2}{i}\left[\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{2}} −\left[\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$=\mathrm{2}+\mathrm{2}{i}\left(\mathrm{2}\right)−\frac{\mathrm{8}}{\mathrm{3}}\:=−\frac{\mathrm{2}}{\mathrm{3}}\:+\mathrm{4}{i}\:. \\ $$
Commented by aliesam last updated on 13/May/19
$${thank}\:{you}\:{sir}\:{great}\:{solution} \\ $$
Commented by MJS last updated on 13/May/19
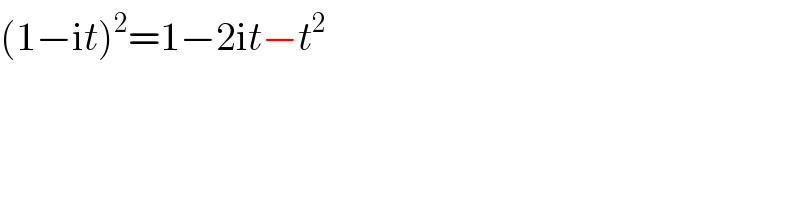
$$\left(\mathrm{1}−\mathrm{i}{t}\right)^{\mathrm{2}} =\mathrm{1}−\mathrm{2i}{t}−{t}^{\mathrm{2}} \\ $$
Commented by aliesam last updated on 13/May/19
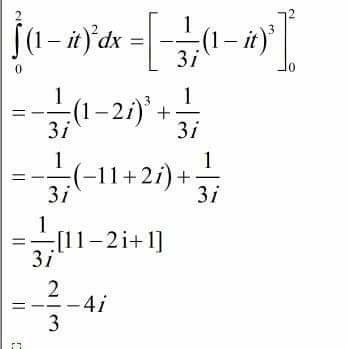
Answered by meme last updated on 13/May/19
![=∫_0 ^2 (1−2it−t^2 )dt(because (a−b)^2 =a^2 −2ab+b^2 or a=1 and b=it) =∫_0 ^2 dt−∫_0 ^2 (2it)dt−∫_0 ^2 t^2 dt =[t]_0 ^2 −[it^2 ]_0 ^2 −3[(1/3)t^3 ]_0 ^2 =2−4i−8 =−7−4i](Q59693.png)
$$=\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{1}−\mathrm{2}{it}−{t}^{\mathrm{2}} \right){dt}\left({because}\:\left({a}−{b}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} −\mathrm{2}{ab}+{b}^{\mathrm{2}} \:{or}\:{a}=\mathrm{1}\:{and}\:{b}={it}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} {dt}−\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{2}{it}\right){dt}−\int_{\mathrm{0}} ^{\mathrm{2}} {t}^{\mathrm{2}} {dt} \\ $$$$=\left[{t}\right]_{\mathrm{0}} ^{\mathrm{2}} −\left[{it}^{\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{2}} −\mathrm{3}\left[\frac{\mathrm{1}}{\mathrm{3}}{t}^{\mathrm{3}} \right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$=\mathrm{2}−\mathrm{4}{i}−\mathrm{8} \\ $$$$=−\mathrm{7}−\mathrm{4}{i} \\ $$
