
Question Number 59655 by aliesam last updated on 13/May/19

Commented by Mr X pcx last updated on 13/May/19
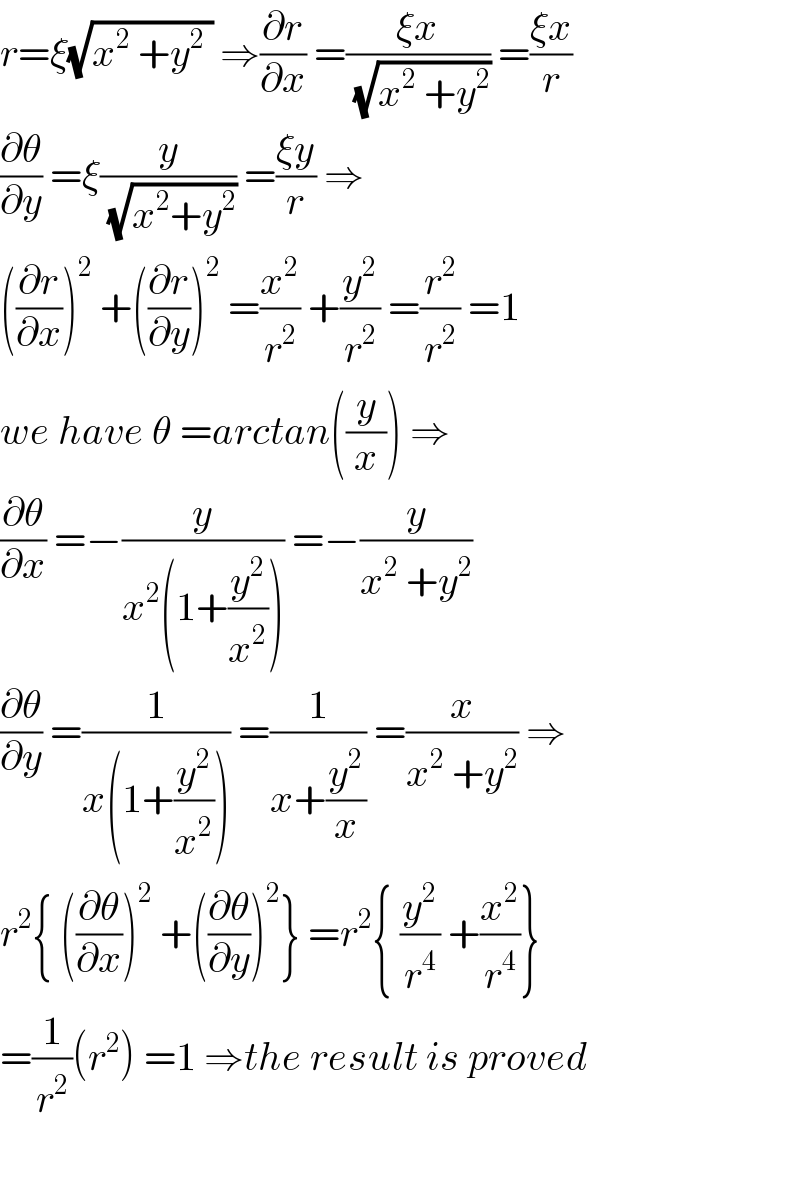
$${r}=\xi\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:}\:\Rightarrow\frac{\partial{r}}{\partial{x}}\:=\frac{\xi{x}}{\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }}\:=\frac{\xi{x}}{{r}} \\ $$$$\frac{\partial\theta}{\partial{y}}\:=\xi\frac{{y}}{\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}\:=\frac{\xi{y}}{{r}}\:\Rightarrow \\ $$$$\left(\frac{\partial{r}}{\partial{x}}\right)^{\mathrm{2}} \:+\left(\frac{\partial{r}}{\partial{y}}\right)^{\mathrm{2}} \:=\frac{{x}^{\mathrm{2}} }{{r}^{\mathrm{2}} }\:+\frac{{y}^{\mathrm{2}} }{{r}^{\mathrm{2}} }\:=\frac{{r}^{\mathrm{2}} }{{r}^{\mathrm{2}} }\:=\mathrm{1} \\ $$$${we}\:{have}\:\theta\:={arctan}\left(\frac{{y}}{{x}}\right)\:\Rightarrow \\ $$$$\frac{\partial\theta}{\partial{x}}\:=−\frac{{y}}{{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)}\:=−\frac{{y}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} } \\ $$$$\frac{\partial\theta}{\partial{y}}\:=\frac{\mathrm{1}}{{x}\left(\mathrm{1}+\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)}\:=\frac{\mathrm{1}}{{x}+\frac{{y}^{\mathrm{2}} }{{x}}}\:=\frac{{x}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }\:\Rightarrow \\ $$$${r}^{\mathrm{2}} \left\{\:\left(\frac{\partial\theta}{\partial{x}}\right)^{\mathrm{2}} \:+\left(\frac{\partial\theta}{\partial{y}}\right)^{\mathrm{2}} \right\}\:={r}^{\mathrm{2}} \left\{\:\frac{{y}^{\mathrm{2}} }{{r}^{\mathrm{4}} }\:+\frac{{x}^{\mathrm{2}} }{{r}^{\mathrm{4}} }\right\} \\ $$$$=\frac{\mathrm{1}}{{r}^{\mathrm{2}} }\left({r}^{\mathrm{2}} \right)\:=\mathrm{1}\:\Rightarrow{the}\:{result}\:{is}\:{proved} \\ $$$$ \\ $$
Commented by aliesam last updated on 13/May/19

$${excellent}.. \\ $$
Commented by Mr X pcx last updated on 13/May/19

$$\xi=\overset{−} {+}\mathrm{1} \\ $$
Answered by tanmay last updated on 13/May/19
![x=rcosθ y=rsinθ r^2 =x^2 +y^2 2r×(∂r/∂x)=2x (∂r/∂x)=(x/r)=cosθ ((∂r/∂x))^2 +((∂r/∂y))^2 =cos^2 θ+sin^2 θ=1 tanθ=(y/x) sec^2 θ×(∂θ/∂x)=(∂/∂x)((y/x)) sec^2 θ×(∂θ/∂x)=((−y)/x^2 ) (∂θ/∂x)=((−rsinθ)/(r^2 cos^2 θ))×(1/(sec^2 θ))=((−sinθ)/r) r((∂θ/∂x))=−sinθ sec^2 θ×(∂θ/∂y)=(1/x)=(1/(rcosθ)) r((∂θ/∂y))=cosθ so r^2 [((∂θ/∂x))^2 +((∂θ/∂y))^2 ] =sin^2 θ+cos^2 θ =1](Q59656.png)
$${x}={rcos}\theta \\ $$$${y}={rsin}\theta \\ $$$${r}^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$$\mathrm{2}{r}×\frac{\partial{r}}{\partial{x}}=\mathrm{2}{x} \\ $$$$\frac{\partial{r}}{\partial{x}}=\frac{{x}}{{r}}={cos}\theta \\ $$$$\left(\frac{\partial{r}}{\partial{x}}\right)^{\mathrm{2}} +\left(\frac{\partial{r}}{\partial{y}}\right)^{\mathrm{2}} ={cos}^{\mathrm{2}} \theta+{sin}^{\mathrm{2}} \theta=\mathrm{1} \\ $$$${tan}\theta=\frac{{y}}{{x}} \\ $$$${sec}^{\mathrm{2}} \theta×\frac{\partial\theta}{\partial{x}}=\frac{\partial}{\partial{x}}\left(\frac{{y}}{{x}}\right) \\ $$$${sec}^{\mathrm{2}} \theta×\frac{\partial\theta}{\partial{x}}=\frac{−{y}}{{x}^{\mathrm{2}} } \\ $$$$\frac{\partial\theta}{\partial{x}}=\frac{−{rsin}\theta}{{r}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta}×\frac{\mathrm{1}}{{sec}^{\mathrm{2}} \theta}=\frac{−{sin}\theta}{{r}} \\ $$$${r}\left(\frac{\partial\theta}{\partial{x}}\right)=−{sin}\theta \\ $$$${sec}^{\mathrm{2}} \theta×\frac{\partial\theta}{\partial{y}}=\frac{\mathrm{1}}{{x}}=\frac{\mathrm{1}}{{rcos}\theta} \\ $$$${r}\left(\frac{\partial\theta}{\partial{y}}\right)={cos}\theta \\ $$$${so}\:{r}^{\mathrm{2}} \left[\left(\frac{\partial\theta}{\partial{x}}\right)^{\mathrm{2}} +\left(\frac{\partial\theta}{\partial{y}}\right)^{\mathrm{2}} \right] \\ $$$$={sin}^{\mathrm{2}} \theta+{cos}^{\mathrm{2}} \theta \\ $$$$=\mathrm{1} \\ $$
Commented by aliesam last updated on 13/May/19
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir} \\ $$
Commented by tanmay last updated on 13/May/19
$${most}\:{welcome}...{yours}\:{questions}\:{are}\:{unique}.. \\ $$
