
Question Number 59620 by ajfour last updated on 12/May/19
Commented by ajfour last updated on 12/May/19

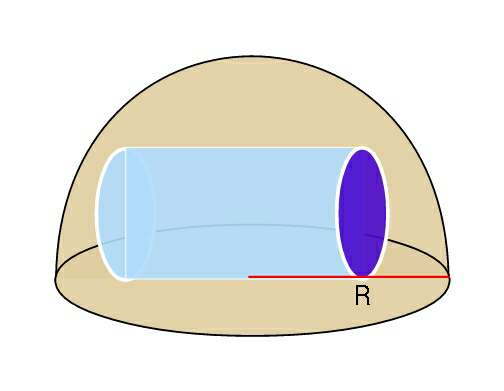
$$\mathrm{Find}\:\mathrm{dimensions}\:\mathrm{of}\:\mathrm{largest}\:\mathrm{volume} \\ $$$$\mathrm{cylinder}\:\mathrm{inscribed}\:\mathrm{within}\:\mathrm{a}\:\mathrm{hemi}- \\ $$$$\mathrm{sphere}\:\mathrm{of}\:\mathrm{radius}\:\mathrm{R}\:\left(\mathrm{in}\:\mathrm{shown}\:\mathrm{orientation}\right). \\ $$
Commented by MJS last updated on 12/May/19

$$\mathrm{more}\:\mathrm{difficult}:\:\mathrm{find}\:\mathrm{the}\:\mathrm{cylinder}\:\mathrm{with}\:\mathrm{the} \\ $$$$\mathrm{largest}\:\mathrm{surface} \\ $$$$\Rightarrow \\ $$$${l}=\frac{\sqrt{\mathrm{34}\left(\mathrm{17}−\sqrt{\mathrm{17}}\right)}}{\mathrm{17}}{R} \\ $$$${r}=\frac{\sqrt{\mathrm{34}\left(\mathrm{17}+\sqrt{\mathrm{17}}\right)}}{\mathrm{68}}{R} \\ $$$${S}=\frac{\pi}{\mathrm{4}}\left(\mathrm{1}+\sqrt{\mathrm{17}}\right){R}^{\mathrm{2}} \\ $$
Answered by MJS last updated on 12/May/19
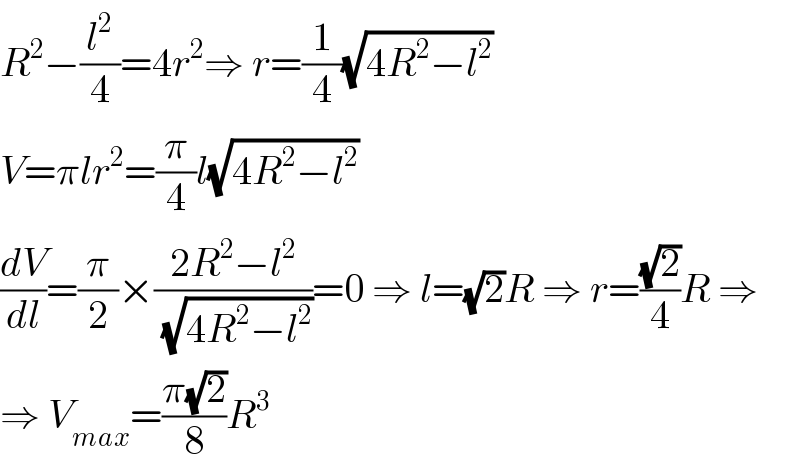
$${R}^{\mathrm{2}} −\frac{{l}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{4}{r}^{\mathrm{2}} \Rightarrow\:{r}=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{l}^{\mathrm{2}} } \\ $$$${V}=\pi{lr}^{\mathrm{2}} =\frac{\pi}{\mathrm{4}}{l}\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{l}^{\mathrm{2}} } \\ $$$$\frac{{dV}}{{dl}}=\frac{\pi}{\mathrm{2}}×\frac{\mathrm{2}{R}^{\mathrm{2}} −{l}^{\mathrm{2}} }{\sqrt{\mathrm{4}{R}^{\mathrm{2}} −{l}^{\mathrm{2}} }}=\mathrm{0}\:\Rightarrow\:{l}=\sqrt{\mathrm{2}}{R}\:\Rightarrow\:{r}=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}{R}\:\Rightarrow \\ $$$$\Rightarrow\:{V}_{{max}} =\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{8}}{R}^{\mathrm{3}} \\ $$
Commented by ajfour last updated on 13/May/19

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}\:!\: \\ $$
