Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 5953 by 314159 last updated on 07/Jun/16

Commented by Rasheed Soomro last updated on 07/Jun/16

Th a nkS!

$$\mathcal{T}{h}\:{a}\:{nk}\mathcal{S}! \\ $$

Commented by Yozzii last updated on 07/Jun/16

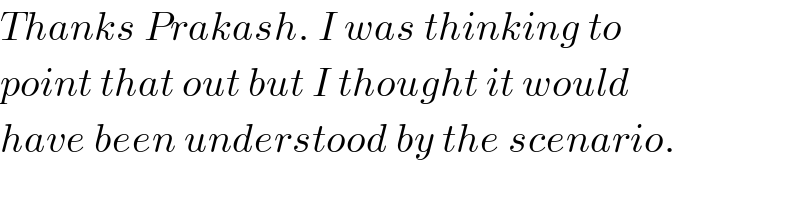
Thanks Prakash. I was thinking to point that out but I thought it would have been understood by the scenario.

$${Thanks}\:{Prakash}.\:{I}\:{was}\:{thinking}\:{to} \\ $$$${point}\:{that}\:{out}\:{but}\:{I}\:{thought}\:{it}\:{would} \\ $$$${have}\:{been}\:{understood}\:{by}\:{the}\:{scenario}. \\ $$

Commented by Yozzii last updated on 07/Jun/16

x^2 −2x+b=0 (1) x^2 −2x+a=0 (2) ((1)&(2) are not simultaneous equations) x∈Q 4a,4b∈Z a−b=2 (a,b)=??? −−−−−−−−−−−−−−−−−−−−−−−− In (1), 4(x^2 −2x)+4b=0 4(x^2 −2x+1−1)+4b=0 4(x−1)^2 +4b−4=0 4(x−1)^2 =4−4b∈Z ⇒x−1=±(1/2)(√(4−4b)) x=1±(1/2)(√(4−4b)) x∈Q⇒4−4b≥0⇒b≤1 and ∃r∈Q where 4−4b=r^2 . b=(1/4)(4−r^2 ) (∗) But, 4−4b∈Z and 4−4b=r^2 ⇒r∈Z. If r where a mixed number or fraction then r^2 ∉Z⇒4−4b∉Z which is a contradiction. Also, a≤1. (∵ x=1±(1/2)(√(4−4a)) in (2)) Since a−b=2 ⇒a=b+2⇒b+2≤1⇒b≤−1. ∴ (∗)⇒(1/4)(4−r^2 )≤−1 4−r^2 ≤−4 r^2 ≥8⇒ r≥2(√2) or r≤−2(√2) Now,a=(1/4)(4−r^2 )+2 a=((4−r^2 +8)/4)=((12−r^2 )/4)≤1 12−r^2 ≤4 r^2 ≥8⇒−2(√2)≤r or r≥2(√2) But for (2), x∈Q ⇒4−4a=n^2 where n∈Z ⇒4−(12−r^2 )=n^2 r^2 −8=n^2 (n,r∈Z) r^2 =n^2 +8 (r−n)(r+n)=8=2^3 =2×4=8×1 If r−n=2⇒r+n=4 2r=6⇒r=3⇒n=1 (r,n)=(3,1) If r−n=4⇒r+n=2⇒r=3⇒n=−1 (r,n)=(3,−1) If r−n=8⇒r+n=1⇒2r=9 which is impossible for r∈Z. If r−n=1⇒r+n=8⇒2r=9 which is impossible. If r−n=−2⇒r+n=−4⇒2r=−6⇒r=−3,n=−1 If r−n=−4,r+n=−2⇒r=−3,n=−1 Only r=±3 or r^2 =9 is possible (and not the entire general set I gave before) ∴ (a,b)=(((12−9)/4),((4−9)/4))=((3/4),((−5)/4))

$${x}^{\mathrm{2}} −\mathrm{2}{x}+{b}=\mathrm{0}\:\:\:\:\left(\mathrm{1}\right) \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}+{a}=\mathrm{0}\:\:\:\:\left(\mathrm{2}\right)\:\:\:\: \\ $$$$\left(\left(\mathrm{1}\right)\&\left(\mathrm{2}\right)\:{are}\:{not}\:{simultaneous}\:{equations}\right) \\ $$$${x}\in\mathbb{Q} \\ $$$$\mathrm{4}{a},\mathrm{4}{b}\in\mathbb{Z} \\ $$$${a}−{b}=\mathrm{2} \\ $$$$\left({a},{b}\right)=??? \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${In}\:\left(\mathrm{1}\right),\:\mathrm{4}\left({x}^{\mathrm{2}} −\mathrm{2}{x}\right)+\mathrm{4}{b}=\mathrm{0} \\ $$$$\mathrm{4}\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}−\mathrm{1}\right)+\mathrm{4}{b}=\mathrm{0} \\ $$$$\mathrm{4}\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}{b}−\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{4}\left({x}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4}−\mathrm{4}{b}\in\mathbb{Z} \\ $$$$\Rightarrow{x}−\mathrm{1}=\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{4}−\mathrm{4}{b}} \\ $$$${x}=\mathrm{1}\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{4}−\mathrm{4}{b}} \\ $$$${x}\in\mathbb{Q}\Rightarrow\mathrm{4}−\mathrm{4}{b}\geqslant\mathrm{0}\Rightarrow{b}\leqslant\mathrm{1} \\ $$$${and}\:\exists{r}\in\mathbb{Q}\:{where}\:\mathrm{4}−\mathrm{4}{b}={r}^{\mathrm{2}} . \\ $$$${b}=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{4}−{r}^{\mathrm{2}} \right)\:\:\:\:\left(\ast\right) \\ $$$${But},\:\mathrm{4}−\mathrm{4}{b}\in\mathbb{Z}\:{and}\:\mathrm{4}−\mathrm{4}{b}={r}^{\mathrm{2}} \Rightarrow{r}\in\mathbb{Z}. \\ $$$${If}\:{r}\:{where}\:{a}\:{mixed}\:{number}\:{or}\:{fraction} \\ $$$${then}\:{r}^{\mathrm{2}} \notin\mathbb{Z}\Rightarrow\mathrm{4}−\mathrm{4}{b}\notin\mathbb{Z}\:{which}\:{is}\:{a}\:{contradiction}. \\ $$$${Also},\:{a}\leqslant\mathrm{1}.\:\left(\because\:{x}=\mathrm{1}\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{4}−\mathrm{4}{a}}\:{in}\:\left(\mathrm{2}\right)\right) \\ $$$${Since}\:{a}−{b}=\mathrm{2} \\ $$$$\Rightarrow{a}={b}+\mathrm{2}\Rightarrow{b}+\mathrm{2}\leqslant\mathrm{1}\Rightarrow{b}\leqslant−\mathrm{1}. \\ $$$$\therefore\:\left(\ast\right)\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{4}−{r}^{\mathrm{2}} \right)\leqslant−\mathrm{1} \\ $$$$\mathrm{4}−{r}^{\mathrm{2}} \leqslant−\mathrm{4} \\ $$$${r}^{\mathrm{2}} \geqslant\mathrm{8}\Rightarrow\:{r}\geqslant\mathrm{2}\sqrt{\mathrm{2}}\:{or}\:{r}\leqslant−\mathrm{2}\sqrt{\mathrm{2}} \\ $$$${Now},{a}=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{4}−{r}^{\mathrm{2}} \right)+\mathrm{2} \\ $$$${a}=\frac{\mathrm{4}−{r}^{\mathrm{2}} +\mathrm{8}}{\mathrm{4}}=\frac{\mathrm{12}−{r}^{\mathrm{2}} }{\mathrm{4}}\leqslant\mathrm{1} \\ $$$$\mathrm{12}−{r}^{\mathrm{2}} \leqslant\mathrm{4} \\ $$$${r}^{\mathrm{2}} \geqslant\mathrm{8}\Rightarrow−\mathrm{2}\sqrt{\mathrm{2}}\leqslant{r}\:{or}\:{r}\geqslant\mathrm{2}\sqrt{\mathrm{2}} \\ $$$${But}\:{for}\:\left(\mathrm{2}\right),\:{x}\in\mathbb{Q}\:\Rightarrow\mathrm{4}−\mathrm{4}{a}={n}^{\mathrm{2}} \:{where}\:{n}\in\mathbb{Z} \\ $$$$\Rightarrow\mathrm{4}−\left(\mathrm{12}−{r}^{\mathrm{2}} \right)={n}^{\mathrm{2}} \\ $$$${r}^{\mathrm{2}} −\mathrm{8}={n}^{\mathrm{2}} \:\:\:\:\:\left({n},{r}\in\mathbb{Z}\right) \\ $$$${r}^{\mathrm{2}} ={n}^{\mathrm{2}} +\mathrm{8} \\ $$$$\left({r}−{n}\right)\left({r}+{n}\right)=\mathrm{8}=\mathrm{2}^{\mathrm{3}} =\mathrm{2}×\mathrm{4}=\mathrm{8}×\mathrm{1} \\ $$$${If}\:{r}−{n}=\mathrm{2}\Rightarrow{r}+{n}=\mathrm{4} \\ $$$$\mathrm{2}{r}=\mathrm{6}\Rightarrow{r}=\mathrm{3}\Rightarrow{n}=\mathrm{1}\:\:\left({r},{n}\right)=\left(\mathrm{3},\mathrm{1}\right) \\ $$$${If}\:{r}−{n}=\mathrm{4}\Rightarrow{r}+{n}=\mathrm{2}\Rightarrow{r}=\mathrm{3}\Rightarrow{n}=−\mathrm{1}\:\:\:\:\left({r},{n}\right)=\left(\mathrm{3},−\mathrm{1}\right) \\ $$$${If}\:{r}−{n}=\mathrm{8}\Rightarrow{r}+{n}=\mathrm{1}\Rightarrow\mathrm{2}{r}=\mathrm{9}\:{which}\:{is}\:{impossible}\:{for}\:{r}\in\mathbb{Z}. \\ $$$${If}\:{r}−{n}=\mathrm{1}\Rightarrow{r}+{n}=\mathrm{8}\Rightarrow\mathrm{2}{r}=\mathrm{9}\:{which}\:{is}\:{impossible}. \\ $$$${If}\:{r}−{n}=−\mathrm{2}\Rightarrow{r}+{n}=−\mathrm{4}\Rightarrow\mathrm{2}{r}=−\mathrm{6}\Rightarrow{r}=−\mathrm{3},{n}=−\mathrm{1} \\ $$$${If}\:{r}−{n}=−\mathrm{4},{r}+{n}=−\mathrm{2}\Rightarrow{r}=−\mathrm{3},{n}=−\mathrm{1} \\ $$$${Only}\:{r}=\pm\mathrm{3}\:{or}\:{r}^{\mathrm{2}} =\mathrm{9}\:{is}\:{possible}\:\left({and}\:{not}\:{the}\:{entire}\:{general}\:{set}\:{I}\:{gave}\:{before}\right) \\ $$$$\therefore\:\left({a},{b}\right)=\left(\frac{\mathrm{12}−\mathrm{9}}{\mathrm{4}},\frac{\mathrm{4}−\mathrm{9}}{\mathrm{4}}\right)=\left(\frac{\mathrm{3}}{\mathrm{4}},\frac{−\mathrm{5}}{\mathrm{4}}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by Rasheed Soomro last updated on 07/Jun/16

x^2 −2x+a=0 (i) x^2 −2x+b=0 (ii) subtracting (ii) from (i) a−b=0 But a−b=2 [given] Isn′t it contradictary?

$${x}^{\mathrm{2}} −\mathrm{2}{x}+{a}=\mathrm{0}\:\:\:\:\left({i}\right) \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}+{b}=\mathrm{0}\:\:\:\:\:\:\left({ii}\right) \\ $$$${subtracting}\:\left({ii}\right)\:{from}\:\left({i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:{a}−{b}=\mathrm{0} \\ $$$${But}\:\:{a}−{b}=\mathrm{2}\:\left[{given}\right] \\ $$$${Isn}'{t}\:{it}\:{contradictary}? \\ $$

Commented by prakash jain last updated on 07/Jun/16

Value of x may be different in two equations. These are not simultaneous equation.

$$\mathrm{Value}\:\mathrm{of}\:{x}\:\mathrm{may}\:\mathrm{be}\:\mathrm{different}\:\mathrm{in}\:\mathrm{two}\:\mathrm{equations}. \\ $$$$\mathrm{These}\:\mathrm{are}\:\mathrm{not}\:\mathrm{simultaneous}\:\mathrm{equation}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com