
Question Number 59516 by naka3546 last updated on 11/May/19
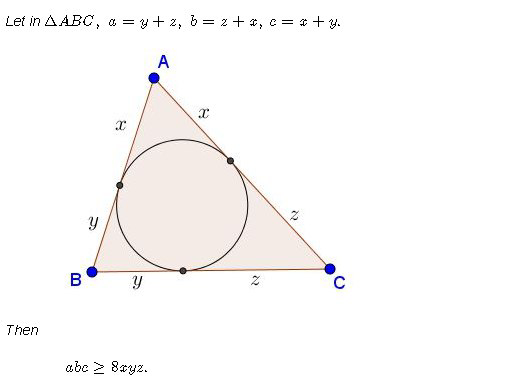
Answered by tanmay last updated on 11/May/19
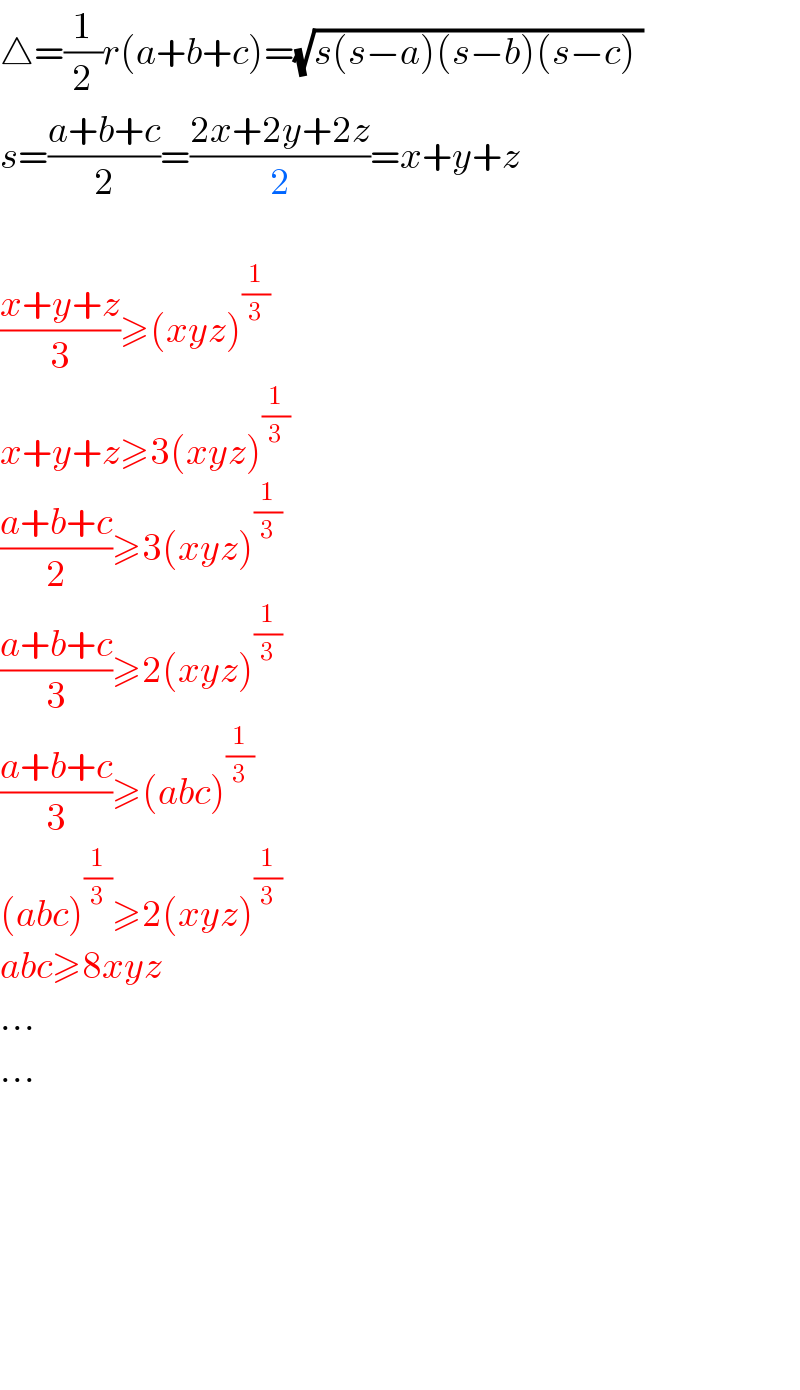
$$\bigtriangleup=\frac{\mathrm{1}}{\mathrm{2}}{r}\left({a}+{b}+{c}\right)=\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)\:} \\ $$$${s}=\frac{{a}+{b}+{c}}{\mathrm{2}}=\frac{\mathrm{2}{x}+\mathrm{2}{y}+\mathrm{2}{z}}{\mathrm{2}}={x}+{y}+{z} \\ $$$$ \\ $$$$\frac{{x}+{y}+{z}}{\mathrm{3}}\geqslant\left({xyz}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${x}+{y}+{z}\geqslant\mathrm{3}\left({xyz}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\frac{{a}+{b}+{c}}{\mathrm{2}}\geqslant\mathrm{3}\left({xyz}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\frac{{a}+{b}+{c}}{\mathrm{3}}\geqslant\mathrm{2}\left({xyz}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\frac{{a}+{b}+{c}}{\mathrm{3}}\geqslant\left({abc}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\left({abc}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \geqslant\mathrm{2}\left({xyz}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${abc}\geqslant\mathrm{8}{xyz} \\ $$$$... \\ $$$$... \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
