
Question Number 59441 by rahul 19 last updated on 10/May/19
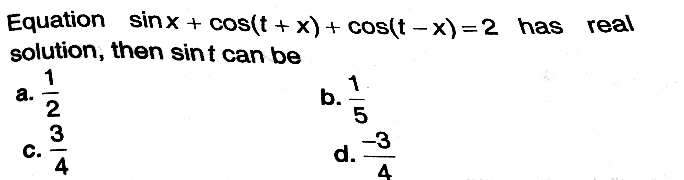
Answered by tanmay last updated on 10/May/19

$${sinx}+\mathrm{2}{costcosx}=\mathrm{2} \\ $$$$\mathrm{4}{cos}^{\mathrm{2}} {t}\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right)=\mathrm{4}−\mathrm{4}{sinx}+{sin}^{\mathrm{2}} {x} \\ $$$${cost}={c}\:\:\:{sinx}={k} \\ $$$$\mathrm{4}{c}^{\mathrm{2}} \left(\mathrm{1}−{k}^{\mathrm{2}} \right)=\mathrm{4}−\mathrm{4}{k}+{k}^{\mathrm{2}} \\ $$$${k}^{\mathrm{2}} +\mathrm{4}{c}^{\mathrm{2}} {k}^{\mathrm{2}} −\mathrm{4}{k}+\mathrm{4}−\mathrm{4}{c}^{\mathrm{2}} =\mathrm{0} \\ $$$${k}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{4}{c}^{\mathrm{2}} \right)+{k}\left(−\mathrm{4}\right)+\mathrm{4}−\mathrm{4}{c}^{\mathrm{2}} =\mathrm{0} \\ $$$${k}=\frac{\mathrm{4}\pm\sqrt{\mathrm{16}−\mathrm{4}×\left(\mathrm{1}+\mathrm{4}{c}^{\mathrm{2}} \right)\left(\mathrm{4}−\mathrm{4}{c}^{\mathrm{2}} \right)}}{\mathrm{2}\left(\mathrm{1}+\mathrm{4}{c}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{4}\pm\sqrt{\mathrm{16}−\mathrm{4}\left(\mathrm{4}−\mathrm{4}{c}^{\mathrm{2}} +\mathrm{16}{c}^{\mathrm{2}} −\mathrm{16}{c}^{\mathrm{4}} \right.}}{\mathrm{2}\left(\mathrm{1}+\mathrm{4}{c}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{4}\pm\sqrt{\mathrm{16}−\mathrm{16}+\mathrm{16}{c}^{\mathrm{2}} −\mathrm{64}{c}^{\mathrm{2}} +\mathrm{64}{c}^{\mathrm{4}} }}{\mathrm{2}\left(\mathrm{1}+\mathrm{4}{c}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{4}\pm\sqrt{\mathrm{64}{c}^{\mathrm{4}} −\mathrm{48}{c}^{\mathrm{2}} }}{\mathrm{2}\left(\mathrm{1}+\mathrm{4}{c}^{\mathrm{2}} \right)} \\ $$$$\mathrm{64}{c}^{\mathrm{4}} −\mathrm{48}{c}^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\mathrm{16}{c}^{\mathrm{2}} \left(\mathrm{4}{c}^{\mathrm{2}} −\mathrm{3}\right)\geqslant\mathrm{0} \\ $$$$\mathrm{16}{c}^{\mathrm{2}} \left(\mathrm{2}{c}+\sqrt{\mathrm{3}}\:\right)\left(\mathrm{2}{c}−\sqrt{\mathrm{3}}\:\right)\geqslant\mathrm{0} \\ $$$${critcal}\:{value}\:{of}\:{c}=\mathrm{0},\frac{\sqrt{\mathrm{3}}}{\mathrm{2}},\frac{−\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${f}\left({c}\right)=\mathrm{16}{c}^{\mathrm{2}} \left(\mathrm{2}{c}+\sqrt{\mathrm{3}}\:\right)\left(\mathrm{2}{c}−\sqrt{\mathrm{3}}\:\right) \\ $$$${f}\left({c}\right)>\mathrm{0}\:\:{when}\:{c}>\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${f}\left({c}\right)>\mathrm{0}\:\:{when}\:{c}<\frac{−\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${f}\left({c}\right)<\mathrm{0}\:\:{when}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}>{c}>\mathrm{0} \\ $$$${f}\left({c}\right)\:<\mathrm{0}\:\:\:\:\:\:{when}\:\mathrm{0}>\:{c}>\frac{−\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${cost}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:\rightarrow{sint}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${rahul}\:{pls}\:{check}\:{mistake}\:{if}\:{any} \\ $$
Commented by rahul 19 last updated on 10/May/19

$${thank}\:{u}\:{sir}. \\ $$
Commented by tanmay last updated on 10/May/19
$${i}\:{want}\:{to}\:{share}\:{some}\:{informationfor}\:{you}...{pls} \\ $$$${reply}\:{if}\:{you}\:{see}\:{this}\:{comment}... \\ $$
Commented by rahul 19 last updated on 10/May/19

$${Sure},{sir}. \\ $$
Commented by tanmay last updated on 10/May/19

$${i}\:{have}\:{found}\:{another}\:{platform}\:{where}\:{you}\:{can} \\ $$$${ask}\:{your}\:{doubt}\:{about}\:{phy}+{chem}+{math}\:{and} \\ $$$${doubt}\:{is}\:{cleared}\:{by}\:{others}\:{just}\:{like}\:{this}\:{platform} \\ $$$${but}\:{in}\:{that}\:{platform}\:{mostly}\:{students}\:{studying} \\ $$$${for}\:{IIT}\:{indian}\:{students}... \\ $$$${if}\:{you}\:{want}\:{i}\:{can}\:{share}... \\ $$
Commented by rahul 19 last updated on 10/May/19
$${i}'{m}\:{sorry},\:{but}\:{it}'{s}\:{too}\:{late}\:{for}\:{me}\:{now}. \\ $$$${just}\:\mathrm{10}−\mathrm{15}\:{days}\:{more}... \\ $$$${Anyways}\:,\:{thanks}\:{for}\:{the}\:{concern}\:! \\ $$
Commented by tanmay last updated on 13/May/19

$${website}\:{goiit}.{com} \\ $$
Commented by necx1 last updated on 13/May/19

$${please}\:{share} \\ $$
