
Question Number 59089 by Tawa1 last updated on 04/May/19

Answered by arcana last updated on 08/Jun/19
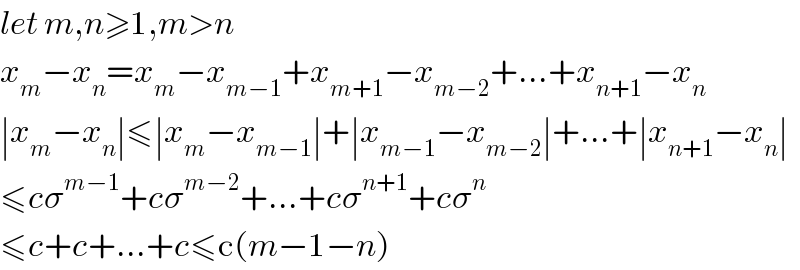
$${let}\:{m},{n}\geqslant\mathrm{1},{m}>{n} \\ $$$${x}_{{m}} −{x}_{{n}} ={x}_{{m}} −{x}_{{m}−\mathrm{1}} +{x}_{{m}+\mathrm{1}} −{x}_{{m}−\mathrm{2}} +...+{x}_{{n}+\mathrm{1}} −{x}_{{n}} \\ $$$$\mid{x}_{{m}} −{x}_{{n}} \mid\leqslant\mid{x}_{{m}} −{x}_{{m}−\mathrm{1}} \mid+\mid{x}_{{m}−\mathrm{1}} −{x}_{{m}−\mathrm{2}} \mid+...+\mid{x}_{{n}+\mathrm{1}} −{x}_{{n}} \mid \\ $$$$\leqslant{c}\sigma^{{m}−\mathrm{1}} +{c}\sigma^{{m}−\mathrm{2}} +...+{c}\sigma^{{n}+\mathrm{1}} +{c}\sigma^{{n}} \\ $$$$\leqslant{c}+{c}+...+{c}\leqslant\mathrm{c}\left({m}−\mathrm{1}−{n}\right) \\ $$
