
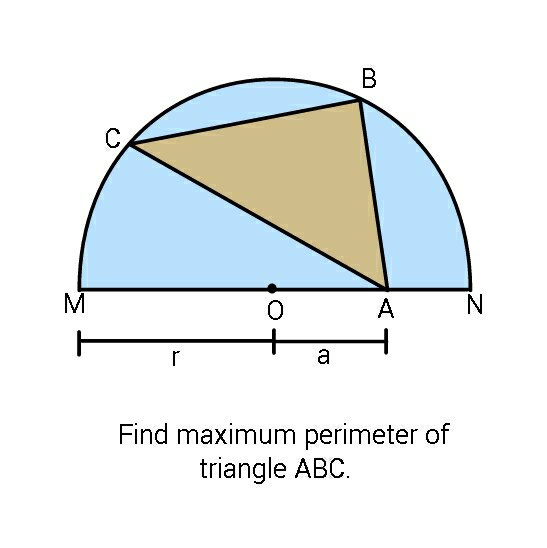
Question Number 58986 by ajfour last updated on 02/May/19
Commented by mr W last updated on 02/May/19
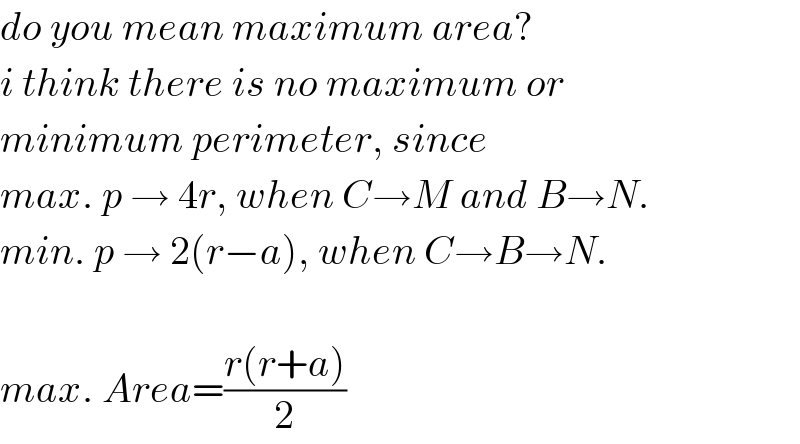
$${do}\:{you}\:{mean}\:{maximum}\:{area}? \\ $$$${i}\:{think}\:{there}\:{is}\:{no}\:{maximum}\:{or} \\ $$$${minimum}\:{perimeter},\:{since} \\ $$$${max}.\:{p}\:\rightarrow\:\mathrm{4}{r},\:{when}\:{C}\rightarrow{M}\:{and}\:{B}\rightarrow{N}. \\ $$$${min}.\:{p}\:\rightarrow\:\mathrm{2}\left({r}−{a}\right),\:{when}\:{C}\rightarrow{B}\rightarrow{N}. \\ $$$$ \\ $$$${max}.\:{Area}=\frac{{r}\left({r}+{a}\right)}{\mathrm{2}} \\ $$
Commented by ajfour last updated on 02/May/19

$$\mathrm{I}\:\mathrm{actually}\:\mathrm{was}\:\mathrm{curious}\:\mathrm{about} \\ $$$$\mathrm{max}\:\mathrm{perimeter}\:\mathrm{itself},\:\mathrm{4r}\:\mathrm{dont}\:\mathrm{seem} \\ $$$$\mathrm{obvious}\:\mathrm{to}\:\mathrm{me}\:\mathrm{Sir}. \\ $$
Commented by mr W last updated on 02/May/19
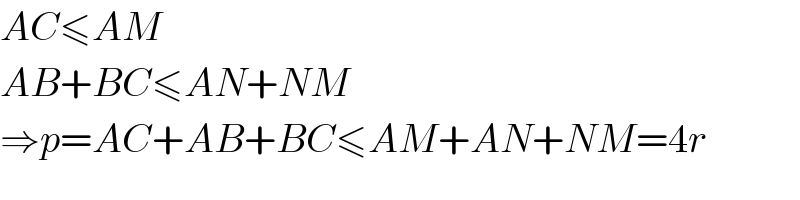
$${AC}\leqslant{AM} \\ $$$${AB}+{BC}\leqslant{AN}+{NM} \\ $$$$\Rightarrow{p}={AC}+{AB}+{BC}\leqslant{AM}+{AN}+{NM}=\mathrm{4}{r} \\ $$
Answered by mr W last updated on 02/May/19
Commented by mr W last updated on 02/May/19
![AB=(√(a^2 +r^2 −2ar cos α)) AC=(√(a^2 +r^2 +2ar cos β )) BC=(√(2r^2 +2r^2 cos (α+β)))=r(√(2[1+cos (α+β)])) p=(√(a^2 +r^2 −2ar cos α))+(√(a^2 +r^2 +2ar cos β ))+r(√(2[1+cos (α+β)])) (∂p/∂α)=((ar sin α)/(√(a^2 +r^2 −2ar cos α)))−r((sin (α+β))/(√(2[1+cos (α+β)])))=0 ⇒((sin α)/(√(1+((r/a))^2 −2((r/a)) cos α)))=((sin (α+β))/(√(2[1+cos (α+β)]))) ⇒((sin α)/(√(1+λ^2 −2λ cos α)))=((sin (α+β))/(√(2[1+cos (α+β)]))) similarly ⇒((−sin β)/(√(1+λ^2 +2λ cos β)))=((sin (α+β))/(√(2[1+cos (α+β)]))) ⇒((sin α)/(√(1+λ^2 −2λ cos α)))=((−sin β)/(√(1+λ^2 +2λ cos β))) with μ=((1+λ^2 )/(2λ)) ⇒((sin α)/(√(μ−cos α)))=((−sin β)/(√(μ+cos β))) ...(i) α=β=0 (180°) fulfill the equations. this is the only solution. if α≠0, β≠0, from (i) we get sin α or sin β must be negative, but this is not possible, since 0≤α,β≤180°, sin α and sin β are always positive. ⇒min. or max. p is when B, C are on the diameter of the circle.](Q58991.png)
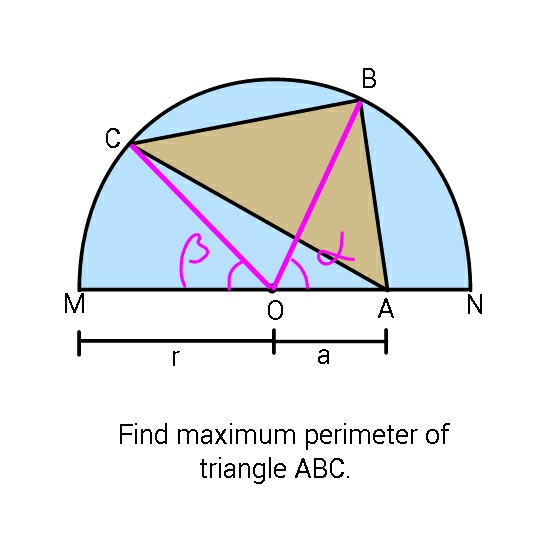
$${AB}=\sqrt{{a}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{ar}\:\mathrm{cos}\:\alpha} \\ $$$${AC}=\sqrt{{a}^{\mathrm{2}} +{r}^{\mathrm{2}} +\mathrm{2}{ar}\:\mathrm{cos}\:\beta\:} \\ $$$${BC}=\sqrt{\mathrm{2}{r}^{\mathrm{2}} +\mathrm{2}{r}^{\mathrm{2}} \mathrm{cos}\:\left(\alpha+\beta\right)}={r}\sqrt{\mathrm{2}\left[\mathrm{1}+\mathrm{cos}\:\left(\alpha+\beta\right)\right]} \\ $$$${p}=\sqrt{{a}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{ar}\:\mathrm{cos}\:\alpha}+\sqrt{{a}^{\mathrm{2}} +{r}^{\mathrm{2}} +\mathrm{2}{ar}\:\mathrm{cos}\:\beta\:}+{r}\sqrt{\mathrm{2}\left[\mathrm{1}+\mathrm{cos}\:\left(\alpha+\beta\right)\right]} \\ $$$$\frac{\partial{p}}{\partial\alpha}=\frac{{ar}\:\mathrm{sin}\:\alpha}{\sqrt{{a}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{ar}\:\mathrm{cos}\:\alpha}}−{r}\frac{\mathrm{sin}\:\left(\alpha+\beta\right)}{\sqrt{\mathrm{2}\left[\mathrm{1}+\mathrm{cos}\:\left(\alpha+\beta\right)\right]}}=\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\alpha}{\sqrt{\mathrm{1}+\left(\frac{{r}}{{a}}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{{r}}{{a}}\right)\:\mathrm{cos}\:\alpha}}=\frac{\mathrm{sin}\:\left(\alpha+\beta\right)}{\sqrt{\mathrm{2}\left[\mathrm{1}+\mathrm{cos}\:\left(\alpha+\beta\right)\right]}} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\alpha}{\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} −\mathrm{2}\lambda\:\mathrm{cos}\:\alpha}}=\frac{\mathrm{sin}\:\left(\alpha+\beta\right)}{\sqrt{\mathrm{2}\left[\mathrm{1}+\mathrm{cos}\:\left(\alpha+\beta\right)\right]}} \\ $$$${similarly} \\ $$$$\Rightarrow\frac{−\mathrm{sin}\:\beta}{\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} +\mathrm{2}\lambda\:\mathrm{cos}\:\beta}}=\frac{\mathrm{sin}\:\left(\alpha+\beta\right)}{\sqrt{\mathrm{2}\left[\mathrm{1}+\mathrm{cos}\:\left(\alpha+\beta\right)\right]}} \\ $$$$ \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\alpha}{\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} −\mathrm{2}\lambda\:\mathrm{cos}\:\alpha}}=\frac{−\mathrm{sin}\:\beta}{\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} +\mathrm{2}\lambda\:\mathrm{cos}\:\beta}} \\ $$$${with}\:\mu=\frac{\mathrm{1}+\lambda^{\mathrm{2}} }{\mathrm{2}\lambda} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\alpha}{\sqrt{\mu−\mathrm{cos}\:\alpha}}=\frac{−\mathrm{sin}\:\beta}{\sqrt{\mu+\mathrm{cos}\:\beta}}\:\:\:...\left({i}\right) \\ $$$$ \\ $$$$\alpha=\beta=\mathrm{0}\:\left(\mathrm{180}°\right)\:{fulfill}\:{the}\:{equations}.\: \\ $$$${this}\:{is}\:{the}\:{only}\:{solution}.\:{if}\:\alpha\neq\mathrm{0},\:\beta\neq\mathrm{0}, \\ $$$${from}\:\left({i}\right)\:{we}\:{get}\:\mathrm{sin}\:\alpha\:{or}\:\mathrm{sin}\:\beta\:{must}\:{be} \\ $$$${negative},\:{but}\:{this}\:{is}\:{not}\:{possible}, \\ $$$${since}\:\mathrm{0}\leqslant\alpha,\beta\leqslant\mathrm{180}°,\:\mathrm{sin}\:\alpha\:{and}\:\mathrm{sin}\:\beta \\ $$$${are}\:{always}\:{positive}. \\ $$$$\Rightarrow{min}.\:{or}\:{max}.\:{p}\:{is}\:{when}\:{B},\:{C}\:{are} \\ $$$${on}\:{the}\:{diameter}\:{of}\:{the}\:{circle}. \\ $$
Commented by ajfour last updated on 03/May/19

$${Thank}\:\mathrm{you}\:\mathrm{sir}.\:\left(\mathrm{you}\:\mathrm{knew}\:\mathrm{it}\:\mathrm{before}\right. \\ $$$$\left.\mathrm{proving},\:\mathrm{and}\:\mathrm{you}\:\mathrm{proved}\:\mathrm{it}\:\mathrm{too}\right). \\ $$
