Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 58675 by ajfour last updated on 27/Apr/19

Commented by ajfour last updated on 27/Apr/19

ABCD is a square; while, PQM is a sector. Find in what proportion are radii b, r, g (blue, red, green respectively).

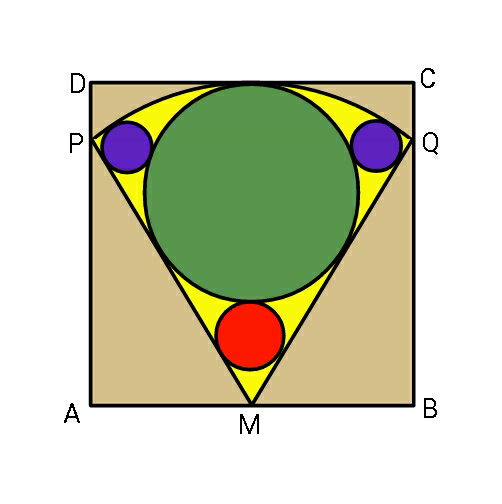
$$\mathrm{ABCD}\:\mathrm{is}\:\mathrm{a}\:\mathrm{square};\:\mathrm{while},\:\mathrm{PQM}\:\mathrm{is} \\ $$$$\mathrm{a}\:\mathrm{sector}.\:\mathrm{Find}\:\mathrm{in}\:\mathrm{what}\:\mathrm{proportion} \\ $$$$\mathrm{are}\:\mathrm{radii}\:\mathrm{b},\:\mathrm{r},\:\mathrm{g}\:\left(\mathrm{blue},\:\mathrm{red},\:\mathrm{green}\right. \\ $$$$\left.\mathrm{respectively}\right). \\ $$

Commented by ajfour last updated on 27/Apr/19

Commented by ajfour last updated on 27/Apr/19

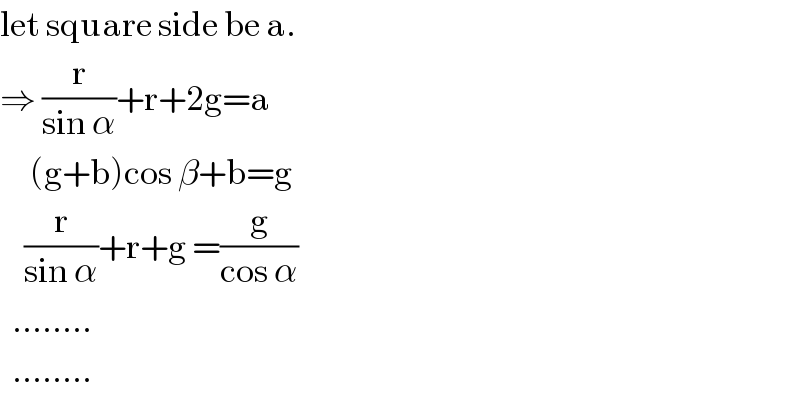
let square side be a. ⇒ (r/(sin α))+r+2g=a (g+b)cos β+b=g (r/(sin α))+r+g =(g/(cos α)) ........ ........

$$\mathrm{let}\:\mathrm{square}\:\mathrm{side}\:\mathrm{be}\:\mathrm{a}. \\ $$$$\Rightarrow\:\frac{\mathrm{r}}{\mathrm{sin}\:\alpha}+\mathrm{r}+\mathrm{2g}=\mathrm{a} \\ $$$$\:\:\:\:\:\left(\mathrm{g}+\mathrm{b}\right)\mathrm{cos}\:\beta+\mathrm{b}=\mathrm{g} \\ $$$$\:\:\:\:\frac{\mathrm{r}}{\mathrm{sin}\:\alpha}+\mathrm{r}+\mathrm{g}\:=\frac{\mathrm{g}}{\mathrm{cos}\:\alpha} \\ $$$$\:\:........ \\ $$$$\:\:........ \\ $$

Commented by mr W last updated on 01/May/19

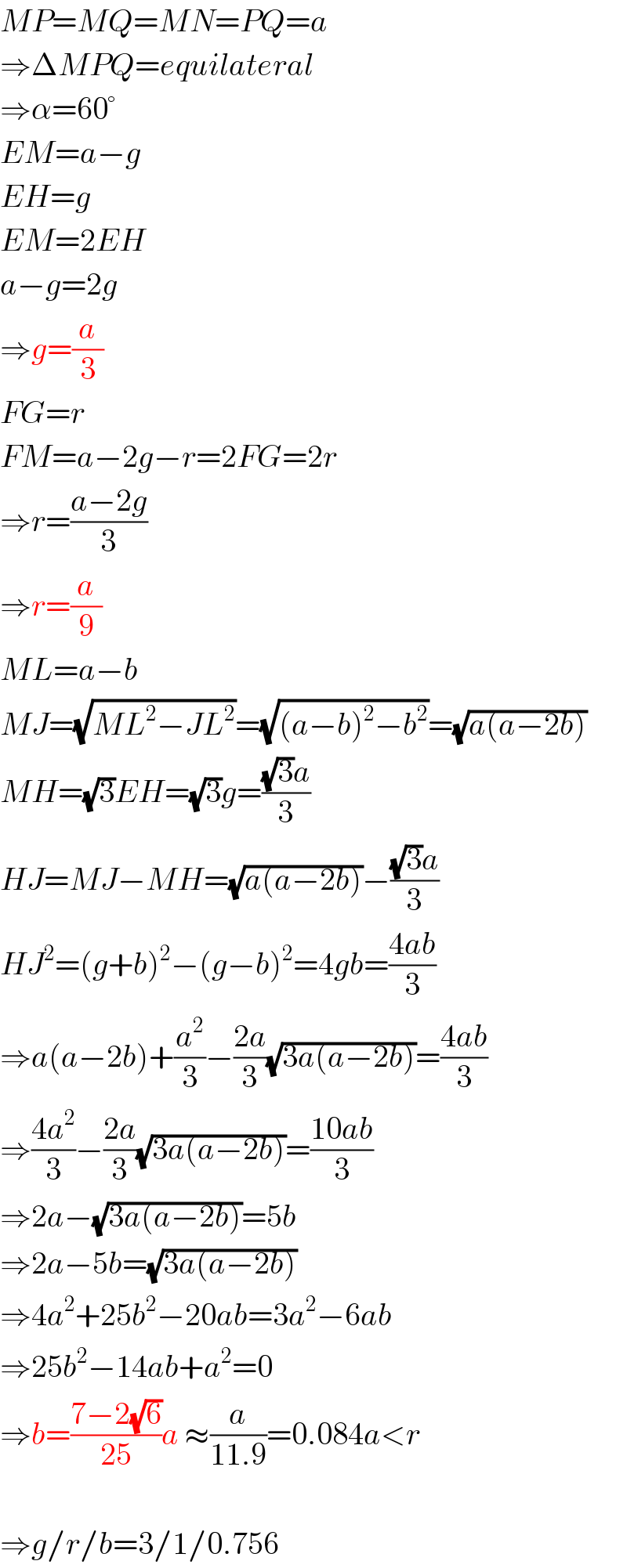
MP=MQ=MN=PQ=a ⇒ΔMPQ=equilateral ⇒α=60° EM=a−g EH=g EM=2EH a−g=2g ⇒g=(a/3) FG=r FM=a−2g−r=2FG=2r ⇒r=((a−2g)/3) ⇒r=(a/9) ML=a−b MJ=(√(ML^2 −JL^2 ))=(√((a−b)^2 −b^2 ))=(√(a(a−2b))) MH=(√3)EH=(√3)g=(((√3)a)/3) HJ=MJ−MH=(√(a(a−2b)))−(((√3)a)/3) HJ^2 =(g+b)^2 −(g−b)^2 =4gb=((4ab)/3) ⇒a(a−2b)+(a^2 /3)−((2a)/3)(√(3a(a−2b)))=((4ab)/3) ⇒((4a^2 )/3)−((2a)/3)(√(3a(a−2b)))=((10ab)/3) ⇒2a−(√(3a(a−2b)))=5b ⇒2a−5b=(√(3a(a−2b))) ⇒4a^2 +25b^2 −20ab=3a^2 −6ab ⇒25b^2 −14ab+a^2 =0 ⇒b=((7−2(√6))/(25))a ≈(a/(11.9))=0.084a<r ⇒g/r/b=3/1/0.756

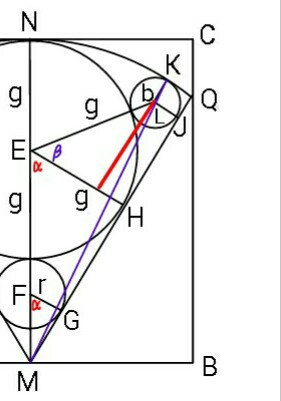
$${MP}={MQ}={MN}={PQ}={a} \\ $$$$\Rightarrow\Delta{MPQ}={equilateral} \\ $$$$\Rightarrow\alpha=\mathrm{60}° \\ $$$${EM}={a}−{g} \\ $$$${EH}={g} \\ $$$${EM}=\mathrm{2}{EH} \\ $$$${a}−{g}=\mathrm{2}{g} \\ $$$$\Rightarrow{g}=\frac{{a}}{\mathrm{3}} \\ $$$${FG}={r} \\ $$$${FM}={a}−\mathrm{2}{g}−{r}=\mathrm{2}{FG}=\mathrm{2}{r} \\ $$$$\Rightarrow{r}=\frac{{a}−\mathrm{2}{g}}{\mathrm{3}} \\ $$$$\Rightarrow{r}=\frac{{a}}{\mathrm{9}} \\ $$$${ML}={a}−{b} \\ $$$${MJ}=\sqrt{{ML}^{\mathrm{2}} −{JL}^{\mathrm{2}} }=\sqrt{\left({a}−{b}\right)^{\mathrm{2}} −{b}^{\mathrm{2}} }=\sqrt{{a}\left({a}−\mathrm{2}{b}\right)} \\ $$$${MH}=\sqrt{\mathrm{3}}{EH}=\sqrt{\mathrm{3}}{g}=\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{3}} \\ $$$${HJ}={MJ}−{MH}=\sqrt{{a}\left({a}−\mathrm{2}{b}\right)}−\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{3}} \\ $$$${HJ}^{\mathrm{2}} =\left({g}+{b}\right)^{\mathrm{2}} −\left({g}−{b}\right)^{\mathrm{2}} =\mathrm{4}{gb}=\frac{\mathrm{4}{ab}}{\mathrm{3}} \\ $$$$\Rightarrow{a}\left({a}−\mathrm{2}{b}\right)+\frac{{a}^{\mathrm{2}} }{\mathrm{3}}−\frac{\mathrm{2}{a}}{\mathrm{3}}\sqrt{\mathrm{3}{a}\left({a}−\mathrm{2}{b}\right)}=\frac{\mathrm{4}{ab}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{\mathrm{4}{a}^{\mathrm{2}} }{\mathrm{3}}−\frac{\mathrm{2}{a}}{\mathrm{3}}\sqrt{\mathrm{3}{a}\left({a}−\mathrm{2}{b}\right)}=\frac{\mathrm{10}{ab}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{2}{a}−\sqrt{\mathrm{3}{a}\left({a}−\mathrm{2}{b}\right)}=\mathrm{5}{b} \\ $$$$\Rightarrow\mathrm{2}{a}−\mathrm{5}{b}=\sqrt{\mathrm{3}{a}\left({a}−\mathrm{2}{b}\right)} \\ $$$$\Rightarrow\mathrm{4}{a}^{\mathrm{2}} +\mathrm{25}{b}^{\mathrm{2}} −\mathrm{20}{ab}=\mathrm{3}{a}^{\mathrm{2}} −\mathrm{6}{ab} \\ $$$$\Rightarrow\mathrm{25}{b}^{\mathrm{2}} −\mathrm{14}{ab}+{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{b}=\frac{\mathrm{7}−\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{25}}{a}\:\approx\frac{{a}}{\mathrm{11}.\mathrm{9}}=\mathrm{0}.\mathrm{084}{a}<{r} \\ $$$$ \\ $$$$\Rightarrow{g}/{r}/{b}=\mathrm{3}/\mathrm{1}/\mathrm{0}.\mathrm{756} \\ $$

Commented by ajfour last updated on 01/May/19

VERY WISE n NICE Sir. Thank you very much!

$$\mathcal{VERY}\:\mathcal{WISE}\:\mathrm{n}\:\mathcal{NICE}\:\:\mathcal{S}{ir}. \\ $$$${Thank}\:{you}\:{very}\:{much}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com