Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 5843 by Rojaye Shegz last updated on 31/May/16

Commented by Rojaye Shegz last updated on 31/May/16

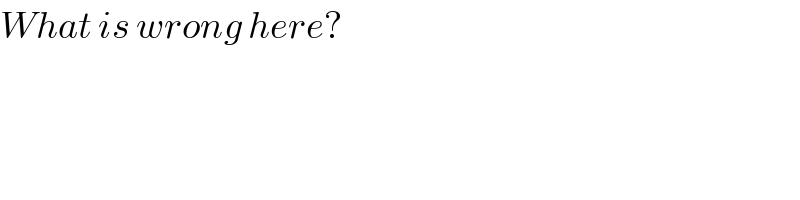
What is wrong here?

$${What}\:{is}\:{wrong}\:{here}? \\ $$

Commented by Yozzii last updated on 31/May/16

∞≠∞

$$\infty\neq\infty\: \\ $$

Commented by prakash jain last updated on 01/Jun/16

1+2+4+8+... is divergent series. Compare it with 1+x+x^2 +....to ∞ S=f(x)=(1/(1−x)) for ∣x∣<1 Analytical continuation of f(x) to x∈R f(2)=(1/(1−2))=−1 So the result 1+2+2^2 +...+to ∞=−1 is valid using analytical continuity. Another way S=1+2+2^2 +...=1+2(1+2+2^2 +..)=1+2S S=1+2S⇒S=−1

$$\mathrm{1}+\mathrm{2}+\mathrm{4}+\mathrm{8}+...\:\mathrm{is}\:\mathrm{divergent}\:\mathrm{series}. \\ $$$$\mathrm{Compare}\:\mathrm{it}\:\mathrm{with}\: \\ $$$$\mathrm{1}+{x}+{x}^{\mathrm{2}} +....\mathrm{to}\:\infty \\ $$$$\mathrm{S}={f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:\mathrm{for}\:\mid{x}\mid<\mathrm{1} \\ $$$$\mathrm{Analytical}\:\mathrm{continuation}\:\mathrm{of}\:{f}\left({x}\right)\:\mathrm{to}\:{x}\in\mathbb{R} \\ $$$${f}\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{2}}=−\mathrm{1} \\ $$$$\mathrm{So}\:\mathrm{the}\:\mathrm{result} \\ $$$$\mathrm{1}+\mathrm{2}+\mathrm{2}^{\mathrm{2}} +...+\mathrm{to}\:\infty=−\mathrm{1}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{valid}}\:\mathrm{using}\:\mathrm{analytical} \\ $$$$\mathrm{continuity}. \\ $$$$\mathrm{Another}\:\mathrm{way} \\ $$$$\mathrm{S}=\mathrm{1}+\mathrm{2}+\mathrm{2}^{\mathrm{2}} +...=\mathrm{1}+\mathrm{2}\left(\mathrm{1}+\mathrm{2}+\mathrm{2}^{\mathrm{2}} +..\right)=\mathrm{1}+\mathrm{2S} \\ $$$$\mathrm{S}=\mathrm{1}+\mathrm{2S}\Rightarrow\mathrm{S}=−\mathrm{1} \\ $$

Commented by prakash jain last updated on 01/Jun/16

The result S=−1 is correct.

$$\mathrm{The}\:\mathrm{result}\:\mathrm{S}=−\mathrm{1}\:\mathrm{is}\:\mathrm{correct}. \\ $$

Commented by FilupSmith last updated on 01/Jun/16

S=−1 is one answer just to make it clear, lim S = ∞ but through analytical continuation S=−1 is correct

$${S}=−\mathrm{1}\:\:\mathrm{is}\:\boldsymbol{{one}}\:\boldsymbol{{answer}} \\ $$$$\mathrm{just}\:\mathrm{to}\:\mathrm{make}\:\mathrm{it}\:\mathrm{clear}, \\ $$$$\mathrm{lim}\:{S}\:=\:\infty \\ $$$$\mathrm{but}\:\mathrm{through}\:\mathrm{analytical}\:\mathrm{continuation} \\ $$$${S}=−\mathrm{1}\:\mathrm{is}\:\mathrm{correct} \\ $$

Commented by Rojaye Shegz last updated on 01/Jun/16

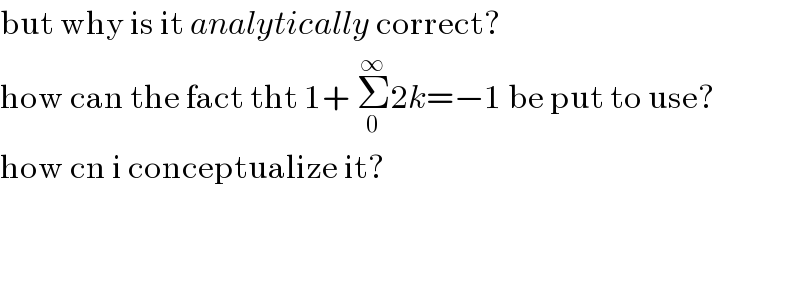
but why is it analytically correct? how can the fact tht 1+ Σ_0 ^∞ 2k=−1 be put to use? how cn i conceptualize it?

$$\mathrm{but}\:\mathrm{why}\:\mathrm{is}\:\mathrm{it}\:{analytically}\:\mathrm{correct}? \\ $$$$\mathrm{how}\:\mathrm{can}\:\mathrm{the}\:\mathrm{fact}\:\mathrm{tht}\:\mathrm{1}+\:\underset{\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{2}{k}=−\mathrm{1}\:\mathrm{be}\:\mathrm{put}\:\mathrm{to}\:\mathrm{use}? \\ $$$$\mathrm{how}\:\mathrm{cn}\:\mathrm{i}\:\mathrm{conceptualize}\:\mathrm{it}? \\ $$$$ \\ $$$$ \\ $$

Commented by FilupSmith last updated on 02/Jun/16

There are aplications in more complex physics for such things. A famous example is: 1+2+3+...=−(1/(12)) This has applications in astrophysics. I don′t have any better examples or specifics. Sometimes people refer to the analytical solution as an algebraic solution. e.g. S=2+4+8+... 2S=4+8+16+... ∴2S+2=S S=−2 ∴ 2+4+8+16+...=−2 is an algebraic solution through analytical continuation. or, another method S=2+4+8+... S=2(1+2+4+...) S=2(1+S) S=2+2S S=−2

$$\mathrm{There}\:\mathrm{are}\:\mathrm{aplications}\:\mathrm{in}\:\mathrm{more}\:\mathrm{complex} \\ $$$$\mathrm{physics}\:\mathrm{for}\:\mathrm{such}\:\mathrm{things}. \\ $$$$\mathrm{A}\:\mathrm{famous}\:\mathrm{example}\:\mathrm{is}:\:\mathrm{1}+\mathrm{2}+\mathrm{3}+...=−\frac{\mathrm{1}}{\mathrm{12}} \\ $$$$\mathrm{This}\:\mathrm{has}\:\mathrm{applications}\:\mathrm{in}\:\mathrm{astrophysics}. \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{have}\:\mathrm{any}\:\mathrm{better}\:\mathrm{examples}\:\mathrm{or}\:\mathrm{specifics}. \\ $$$$ \\ $$$$\mathrm{Sometimes}\:\mathrm{people}\:\mathrm{refer}\:\mathrm{to}\:\mathrm{the}\:\mathrm{analytical} \\ $$$$\mathrm{solution}\:\mathrm{as}\:\mathrm{an}\:\mathrm{algebraic}\:\mathrm{solution}. \\ $$$$ \\ $$$$\mathrm{e}.\mathrm{g}. \\ $$$${S}=\mathrm{2}+\mathrm{4}+\mathrm{8}+... \\ $$$$\mathrm{2}{S}=\mathrm{4}+\mathrm{8}+\mathrm{16}+... \\ $$$$\therefore\mathrm{2}{S}+\mathrm{2}={S} \\ $$$${S}=−\mathrm{2} \\ $$$$\therefore\:\mathrm{2}+\mathrm{4}+\mathrm{8}+\mathrm{16}+...=−\mathrm{2}\:\mathrm{is}\:\mathrm{an}\:\mathrm{algebraic}\:\mathrm{solution} \\ $$$$\mathrm{through}\:\mathrm{analytical}\:\mathrm{continuation}. \\ $$$$ \\ $$$${or},\:\mathrm{another}\:\mathrm{method} \\ $$$${S}=\mathrm{2}+\mathrm{4}+\mathrm{8}+... \\ $$$${S}=\mathrm{2}\left(\mathrm{1}+\mathrm{2}+\mathrm{4}+...\right) \\ $$$${S}=\mathrm{2}\left(\mathrm{1}+{S}\right) \\ $$$${S}=\mathrm{2}+\mathrm{2}{S} \\ $$$${S}=−\mathrm{2} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com