Question and Answers Forum

All Questions      Topic List

Optics Questions

Previous in All Question      Next in All Question      

Previous in Optics      Next in Optics      

Question Number 54357 by ajfour last updated on 02/Feb/19

Commented by ajfour last updated on 02/Feb/19

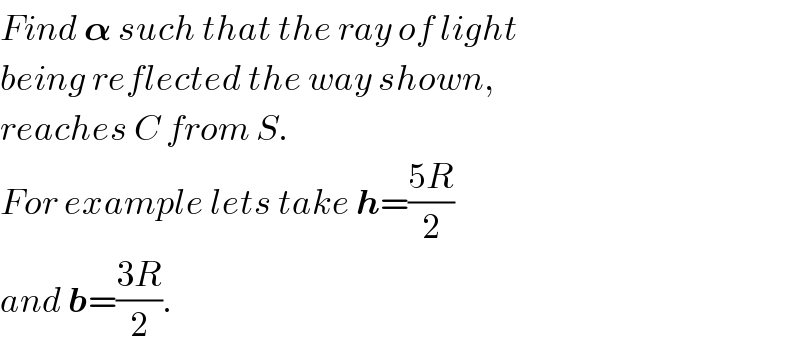
Find 𝛂 such that the ray of light being reflected the way shown, reaches C from S. For example lets take h=((5R)/2) and b=((3R)/2).

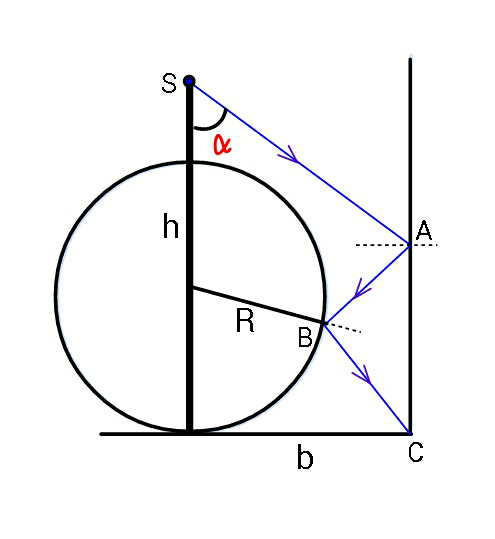
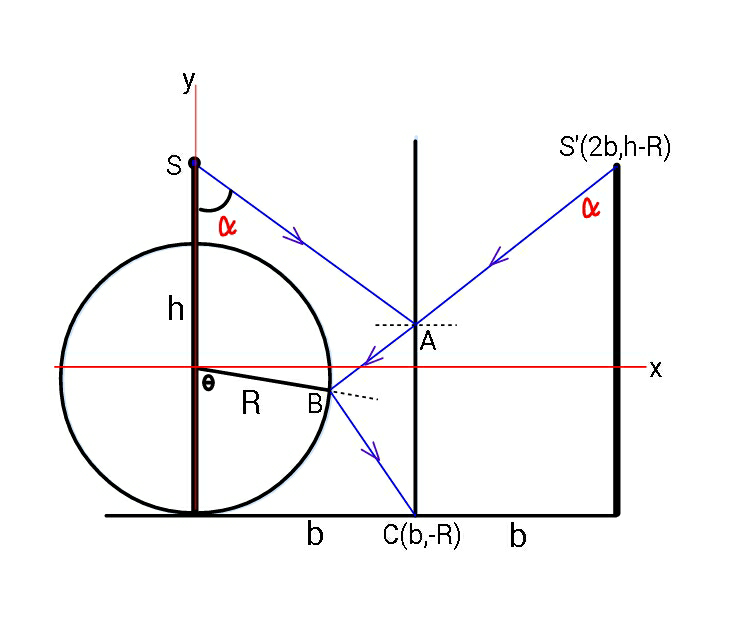
$${Find}\:\boldsymbol{\alpha}\:{such}\:{that}\:{the}\:{ray}\:{of}\:{light} \\ $$$${being}\:{reflected}\:{the}\:{way}\:{shown}, \\ $$$${reaches}\:{C}\:{from}\:{S}. \\ $$$${For}\:{example}\:{lets}\:{take}\:\boldsymbol{{h}}=\frac{\mathrm{5}{R}}{\mathrm{2}} \\ $$$${and}\:\boldsymbol{{b}}=\frac{\mathrm{3}{R}}{\mathrm{2}}. \\ $$

Answered by mr W last updated on 02/Feb/19

Commented by mr W last updated on 03/Feb/19

let δ=(b/R), λ=(h/R) α−β=(π/2)−θ ⇒β=α+θ−(π/2) (2b−R sin θ)(1/(tan α))+R(1−cos θ)=h ⇒tan α=((2b−R sin θ)/(h−R(1−cos θ)))=((2δ−sin θ)/(λ−1+cos θ)) (b−R tan (θ/2))(1/(sin β))=(R tan (θ/2))(1/(sin (θ+β))) (b−R tan (θ/2))(1/(sin (θ+α−(π/2))))=(R tan (θ/2))(1/(sin (2θ+α−(π/2)))) ((δ/(tan (θ/2)))−1)((cos (2θ+α))/(cos (θ+α)))=1 ((δ/(tan (θ/2)))−1)((cos 2θ−sin 2θ tan α)/(cos θ−sin θ tan α))=1 ((δ/(tan (θ/2)))−1)((cos 2θ−sin 2θ((2δ−sin θ)/(λ−1+cos θ)))/(cos θ−sin θ((2b−R sin θ)/(h−R(1−cos θ)))))=1 ⇒((δ/(tan (θ/2)))−1)(((cos 2θ)(λ−1+cos θ)−(sin 2θ)(2δ−sin θ))/((cos θ)(λ−1+cos θ)−(sin θ)(2δ−sin θ)))=1 ⇒θ=.... example: δ=(b/R)=(3/2), λ=(h/R)=(5/2) ⇒θ=80.5644°⇒α=50.4304°

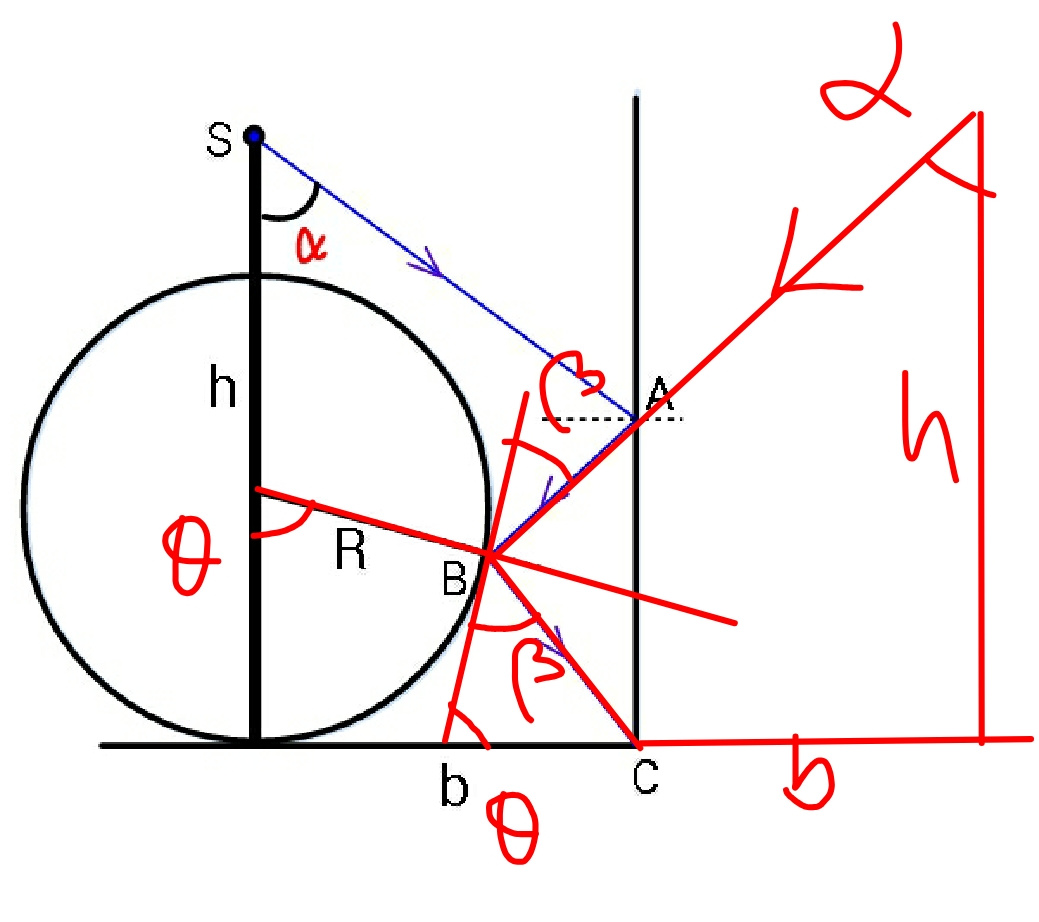
$${let}\:\delta=\frac{{b}}{{R}},\:\lambda=\frac{{h}}{{R}} \\ $$$$\alpha−\beta=\frac{\pi}{\mathrm{2}}−\theta \\ $$$$\Rightarrow\beta=\alpha+\theta−\frac{\pi}{\mathrm{2}} \\ $$$$\left(\mathrm{2}{b}−{R}\:\mathrm{sin}\:\theta\right)\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}+{R}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)={h} \\ $$$$\Rightarrow\mathrm{tan}\:\alpha=\frac{\mathrm{2}{b}−{R}\:\mathrm{sin}\:\theta}{{h}−{R}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}=\frac{\mathrm{2}\delta−\mathrm{sin}\:\theta}{\lambda−\mathrm{1}+\mathrm{cos}\:\theta} \\ $$$$\left({b}−{R}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\right)\frac{\mathrm{1}}{\mathrm{sin}\:\beta}=\left({R}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\right)\frac{\mathrm{1}}{\mathrm{sin}\:\left(\theta+\beta\right)} \\ $$$$\left({b}−{R}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\right)\frac{\mathrm{1}}{\mathrm{sin}\:\left(\theta+\alpha−\frac{\pi}{\mathrm{2}}\right)}=\left({R}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\right)\frac{\mathrm{1}}{\mathrm{sin}\:\left(\mathrm{2}\theta+\alpha−\frac{\pi}{\mathrm{2}}\right)} \\ $$$$\left(\frac{\delta}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}−\mathrm{1}\right)\frac{\mathrm{cos}\:\left(\mathrm{2}\theta+\alpha\right)}{\mathrm{cos}\:\left(\theta+\alpha\right)}=\mathrm{1} \\ $$$$\left(\frac{\delta}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}−\mathrm{1}\right)\frac{\mathrm{cos}\:\mathrm{2}\theta−\mathrm{sin}\:\mathrm{2}\theta\:\mathrm{tan}\:\alpha}{\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\:\mathrm{tan}\:\alpha}=\mathrm{1} \\ $$$$\left(\frac{\delta}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}−\mathrm{1}\right)\frac{\mathrm{cos}\:\mathrm{2}\theta−\mathrm{sin}\:\mathrm{2}\theta\frac{\mathrm{2}\delta−\mathrm{sin}\:\theta}{\lambda−\mathrm{1}+\mathrm{cos}\:\theta}}{\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\frac{\mathrm{2}{b}−{R}\:\mathrm{sin}\:\theta}{{h}−{R}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}}=\mathrm{1} \\ $$$$\Rightarrow\left(\frac{\delta}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}−\mathrm{1}\right)\frac{\left(\mathrm{cos}\:\mathrm{2}\theta\right)\left(\lambda−\mathrm{1}+\mathrm{cos}\:\theta\right)−\left(\mathrm{sin}\:\mathrm{2}\theta\right)\left(\mathrm{2}\delta−\mathrm{sin}\:\theta\right)}{\left(\mathrm{cos}\:\theta\right)\left(\lambda−\mathrm{1}+\mathrm{cos}\:\theta\right)−\left(\mathrm{sin}\:\theta\right)\left(\mathrm{2}\delta−\mathrm{sin}\:\theta\right)}=\mathrm{1} \\ $$$$\Rightarrow\theta=.... \\ $$$${example}: \\ $$$$\delta=\frac{{b}}{{R}}=\frac{\mathrm{3}}{\mathrm{2}},\:\lambda=\frac{{h}}{{R}}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\Rightarrow\theta=\mathrm{80}.\mathrm{5644}°\Rightarrow\alpha=\mathrm{50}.\mathrm{4304}° \\ $$

Commented by ajfour last updated on 03/Feb/19

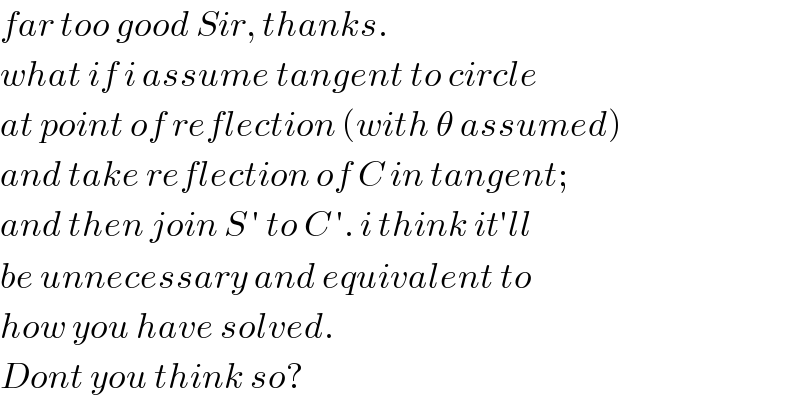
far too good Sir, thanks. what if i assume tangent to circle at point of reflection (with θ assumed) and take reflection of C in tangent; and then join S ′ to C ′. i think it′ll be unnecessary and equivalent to how you have solved. Dont you think so?

$${far}\:{too}\:{good}\:{Sir},\:{thanks}. \\ $$$${what}\:{if}\:{i}\:{assume}\:{tangent}\:{to}\:{circle} \\ $$$${at}\:{point}\:{of}\:{reflection}\:\left({with}\:\theta\:{assumed}\right) \\ $$$${and}\:{take}\:{reflection}\:{of}\:{C}\:{in}\:{tangent}; \\ $$$${and}\:{then}\:{join}\:{S}\:'\:{to}\:{C}\:'.\:{i}\:{think}\:{it}'{ll} \\ $$$${be}\:{unnecessary}\:{and}\:{equivalent}\:{to} \\ $$$${how}\:{you}\:{have}\:{solved}. \\ $$$${Dont}\:{you}\:{think}\:{so}? \\ $$

Commented by mr W last updated on 03/Feb/19

that′s correct sir. i considered it too, but this doesn′t help so much if we try to solve with trigonometrical method. but it helps more if we try to use coordinate method.

$${that}'{s}\:{correct}\:{sir}.\:\: \\ $$$${i}\:{considered}\:{it}\:{too},\:\:{but}\:{this}\:{doesn}'{t} \\ $$$${help}\:{so}\:{much}\:{if}\:{we}\:{try}\:{to}\:{solve}\:{with} \\ $$$${trigonometrical}\:{method}.\:\:{but}\:{it}\:{helps} \\ $$$${more}\:{if}\:{we}\:{try}\:{to}\:{use}\:{coordinate} \\ $$$${method}. \\ $$

Answered by ajfour last updated on 03/Feb/19

Commented by ajfour last updated on 03/Feb/19

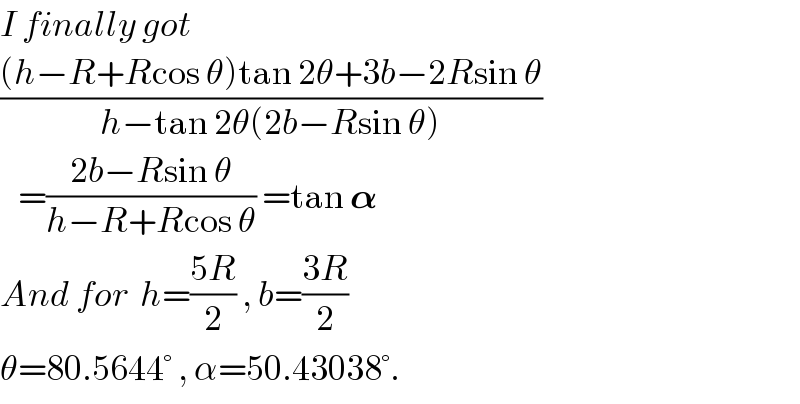
I finally got (((h−R+Rcos θ)tan 2θ+3b−2Rsin θ)/(h−tan 2θ(2b−Rsin θ))) =((2b−Rsin θ)/(h−R+Rcos θ)) =tan 𝛂 And for h=((5R)/2) , b=((3R)/2) θ=80.5644° , α=50.43038°.

$${I}\:{finally}\:{got} \\ $$$$\frac{\left({h}−{R}+{R}\mathrm{cos}\:\theta\right)\mathrm{tan}\:\mathrm{2}\theta+\mathrm{3}{b}−\mathrm{2}{R}\mathrm{sin}\:\theta}{{h}−\mathrm{tan}\:\mathrm{2}\theta\left(\mathrm{2}{b}−{R}\mathrm{sin}\:\theta\right)} \\ $$$$\:\:\:=\frac{\mathrm{2}{b}−{R}\mathrm{sin}\:\theta}{{h}−{R}+{R}\mathrm{cos}\:\theta}\:=\mathrm{tan}\:\boldsymbol{\alpha} \\ $$$${And}\:{for}\:\:{h}=\frac{\mathrm{5}{R}}{\mathrm{2}}\:,\:{b}=\frac{\mathrm{3}{R}}{\mathrm{2}} \\ $$$$\theta=\mathrm{80}.\mathrm{5644}°\:,\:\alpha=\mathrm{50}.\mathrm{43038}°. \\ $$

Commented by mr W last updated on 03/Feb/19

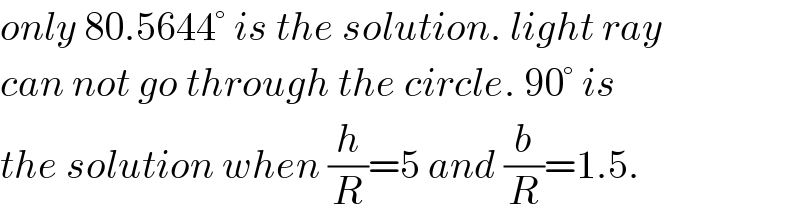
only 80.5644° is the solution. light ray can not go through the circle. 90° is the solution when (h/R)=5 and (b/R)=1.5.

$${only}\:\mathrm{80}.\mathrm{5644}°\:{is}\:{the}\:{solution}.\:{light}\:{ray} \\ $$$${can}\:{not}\:{go}\:{through}\:{the}\:{circle}.\:\mathrm{90}°\:{is} \\ $$$${the}\:{solution}\:{when}\:\frac{{h}}{{R}}=\mathrm{5}\:{and}\:\frac{{b}}{{R}}=\mathrm{1}.\mathrm{5}. \\ $$

Commented by ajfour last updated on 03/Feb/19

yes Sir, you are right.

$${yes}\:{Sir},\:{you}\:{are}\:{right}. \\ $$

Commented by mr W last updated on 03/Feb/19

B(R sin θ,−R cos θ) slope of OB: tan ϕ_(OB) =−(1/(tan θ)) slope of BS′: tan ϕ_(BS′) =((h−R+R cos θ)/(2b−R sin θ)) slope of BC: tan ϕ_(BC) =((−R+R cos θ)/(b−R sin θ)) ϕ_(BS′) −ϕ_(OB) =ϕ_(OB) −ϕ_(BC) tan (ϕ_(BS′) −ϕ_(OB) )=tan (ϕ_(OB) −ϕ_(BC) ) ((((h−R+R cos θ)/(2b−R sin θ))+(1/(tan θ)))/(1−((h−R+R cos θ)/(2b−R sin θ))×(1/(tan θ))))=((−(1/(tan θ))−((−R+R cos θ)/(b−R sin θ)))/(1−(1/(tan θ))×((−R+R cos θ)/(b−R sin θ)))) (((h−R+R cos θ)sin θ+(2b−R sin θ)cos θ)/((2b−R sin θ)sin θ−(h−R+R cos θ)cos θ))=((R(1−cos θ)sin θ−(b−R sin θ)cos θ)/((b−R sin θ)sin θ+R(1−cos θ)cos θ)) (((h−R)sin θ+2b cos θ)/(2b sin θ−(h−R)cos θ−R))=((R sin θ−b cos θ)/(b sin θ+R cos θ−R)) ⇒(((λ−1)sin θ+2δ cos θ)/(2δ sin θ−(λ−1)cos θ−1))=((sin θ−δ cos θ)/(δ sin θ+cos θ−1))

$${B}\left({R}\:\mathrm{sin}\:\theta,−{R}\:\mathrm{cos}\:\theta\right) \\ $$$${slope}\:{of}\:{OB}: \\ $$$$\mathrm{tan}\:\varphi_{{OB}} =−\frac{\mathrm{1}}{\mathrm{tan}\:\theta} \\ $$$${slope}\:{of}\:{BS}': \\ $$$$\mathrm{tan}\:\varphi_{{BS}'} =\frac{{h}−{R}+{R}\:\mathrm{cos}\:\theta}{\mathrm{2}{b}−{R}\:\mathrm{sin}\:\theta} \\ $$$${slope}\:{of}\:{BC}: \\ $$$$\mathrm{tan}\:\varphi_{{BC}} =\frac{−{R}+{R}\:\mathrm{cos}\:\theta}{{b}−{R}\:\mathrm{sin}\:\theta} \\ $$$$\varphi_{{BS}'} −\varphi_{{OB}} =\varphi_{{OB}} −\varphi_{{BC}} \\ $$$$\mathrm{tan}\:\left(\varphi_{{BS}'} −\varphi_{{OB}} \right)=\mathrm{tan}\:\left(\varphi_{{OB}} −\varphi_{{BC}} \right) \\ $$$$\frac{\frac{{h}−{R}+{R}\:\mathrm{cos}\:\theta}{\mathrm{2}{b}−{R}\:\mathrm{sin}\:\theta}+\frac{\mathrm{1}}{\mathrm{tan}\:\theta}}{\mathrm{1}−\frac{{h}−{R}+{R}\:\mathrm{cos}\:\theta}{\mathrm{2}{b}−{R}\:\mathrm{sin}\:\theta}×\frac{\mathrm{1}}{\mathrm{tan}\:\theta}}=\frac{−\frac{\mathrm{1}}{\mathrm{tan}\:\theta}−\frac{−{R}+{R}\:\mathrm{cos}\:\theta}{{b}−{R}\:\mathrm{sin}\:\theta}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:\theta}×\frac{−{R}+{R}\:\mathrm{cos}\:\theta}{{b}−{R}\:\mathrm{sin}\:\theta}} \\ $$$$\frac{\left({h}−{R}+{R}\:\mathrm{cos}\:\theta\right)\mathrm{sin}\:\theta+\left(\mathrm{2}{b}−{R}\:\mathrm{sin}\:\theta\right)\mathrm{cos}\:\theta}{\left(\mathrm{2}{b}−{R}\:\mathrm{sin}\:\theta\right)\mathrm{sin}\:\theta−\left({h}−{R}+{R}\:\mathrm{cos}\:\theta\right)\mathrm{cos}\:\theta}=\frac{{R}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\mathrm{sin}\:\theta−\left({b}−{R}\:\mathrm{sin}\:\theta\right)\mathrm{cos}\:\theta}{\left({b}−{R}\:\mathrm{sin}\:\theta\right)\mathrm{sin}\:\theta+{R}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\mathrm{cos}\:\theta} \\ $$$$\frac{\left({h}−{R}\right)\mathrm{sin}\:\theta+\mathrm{2}{b}\:\mathrm{cos}\:\theta}{\mathrm{2}{b}\:\mathrm{sin}\:\theta−\left({h}−{R}\right)\mathrm{cos}\:\theta−{R}}=\frac{{R}\:\mathrm{sin}\:\theta−{b}\:\mathrm{cos}\:\theta}{{b}\:\mathrm{sin}\:\theta+{R}\:\mathrm{cos}\:\theta−{R}} \\ $$$$\Rightarrow\frac{\left(\lambda−\mathrm{1}\right)\mathrm{sin}\:\theta+\mathrm{2}\delta\:\mathrm{cos}\:\theta}{\mathrm{2}\delta\:\mathrm{sin}\:\theta−\left(\lambda−\mathrm{1}\right)\mathrm{cos}\:\theta−\mathrm{1}}=\frac{\mathrm{sin}\:\theta−\delta\:\mathrm{cos}\:\theta}{\delta\:\mathrm{sin}\:\theta+\mathrm{cos}\:\theta−\mathrm{1}} \\ $$

Commented by ajfour last updated on 04/Feb/19

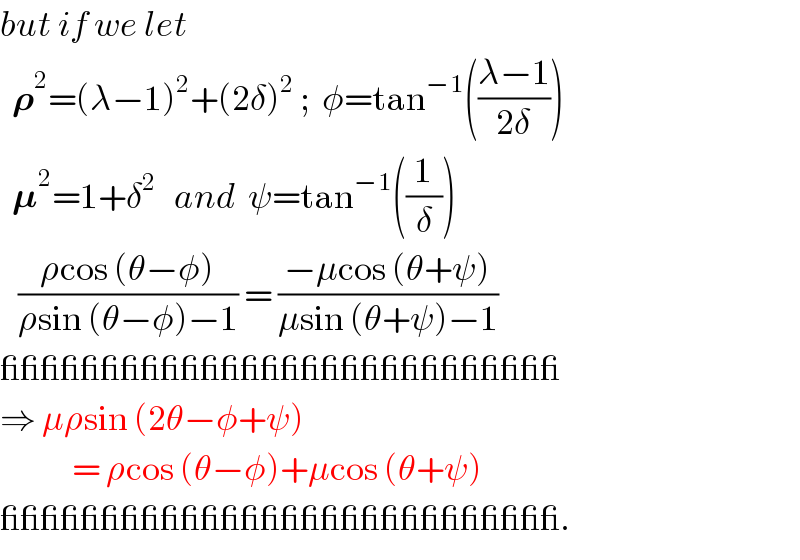
but if we let 𝛒^2 =(λ−1)^2 +(2δ)^2 ; φ=tan^(−1) (((λ−1)/(2δ))) 𝛍^2 =1+δ^2 and ψ=tan^(−1) ((1/δ)) ((ρcos (θ−φ))/(ρsin (θ−φ)−1)) = ((−μcos (θ+ψ))/(μsin (θ+ψ)−1)) ____________________________ ⇒ μρsin (2θ−φ+ψ) = ρcos (θ−φ)+μcos (θ+ψ) ____________________________.

$${but}\:{if}\:{we}\:{let} \\ $$$$\:\:\boldsymbol{\rho}^{\mathrm{2}} =\left(\lambda−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{2}\delta\right)^{\mathrm{2}} \:;\:\:\phi=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\lambda−\mathrm{1}}{\mathrm{2}\delta}\right) \\ $$$$\:\:\boldsymbol{\mu}^{\mathrm{2}} =\mathrm{1}+\delta^{\mathrm{2}} \:\:\:{and}\:\:\psi=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\delta}\right) \\ $$$$\:\:\:\frac{\rho\mathrm{cos}\:\left(\theta−\phi\right)}{\rho\mathrm{sin}\:\left(\theta−\phi\right)−\mathrm{1}}\:=\:\frac{−\mu\mathrm{cos}\:\left(\theta+\psi\right)}{\mu\mathrm{sin}\:\left(\theta+\psi\right)−\mathrm{1}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\Rightarrow\:\mu\rho\mathrm{sin}\:\left(\mathrm{2}\theta−\phi+\psi\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\rho\mathrm{cos}\:\left(\theta−\phi\right)+\mu\mathrm{cos}\:\left(\theta+\psi\right)\: \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_. \\ $$

Commented by mr W last updated on 04/Feb/19

best form for result!

$${best}\:{form}\:{for}\:{result}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com