Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 53828 by ajfour last updated on 26/Jan/19

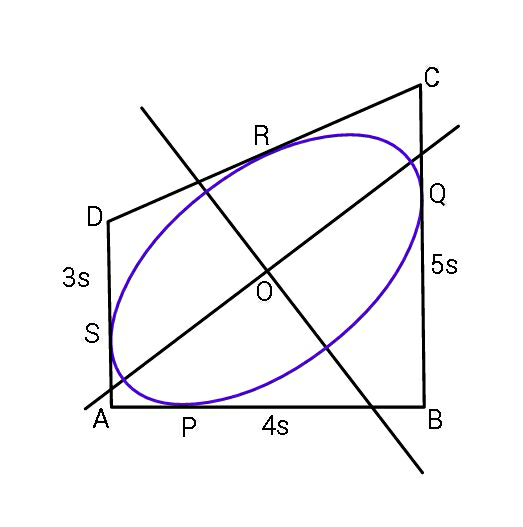
Commented by ajfour last updated on 26/Jan/19

Find a and b of maximum area ellipse within the trapezium.

$${Find}\:{a}\:{and}\:{b}\:{of}\:{maximum}\:{area}\:{ellipse} \\ $$$${within}\:{the}\:{trapezium}. \\ $$

Answered by ajfour last updated on 26/Jan/19

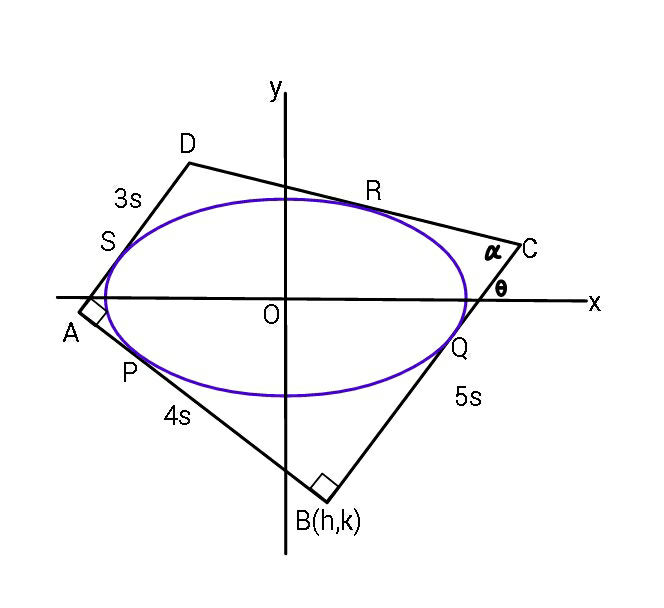
Commented by ajfour last updated on 26/Jan/19

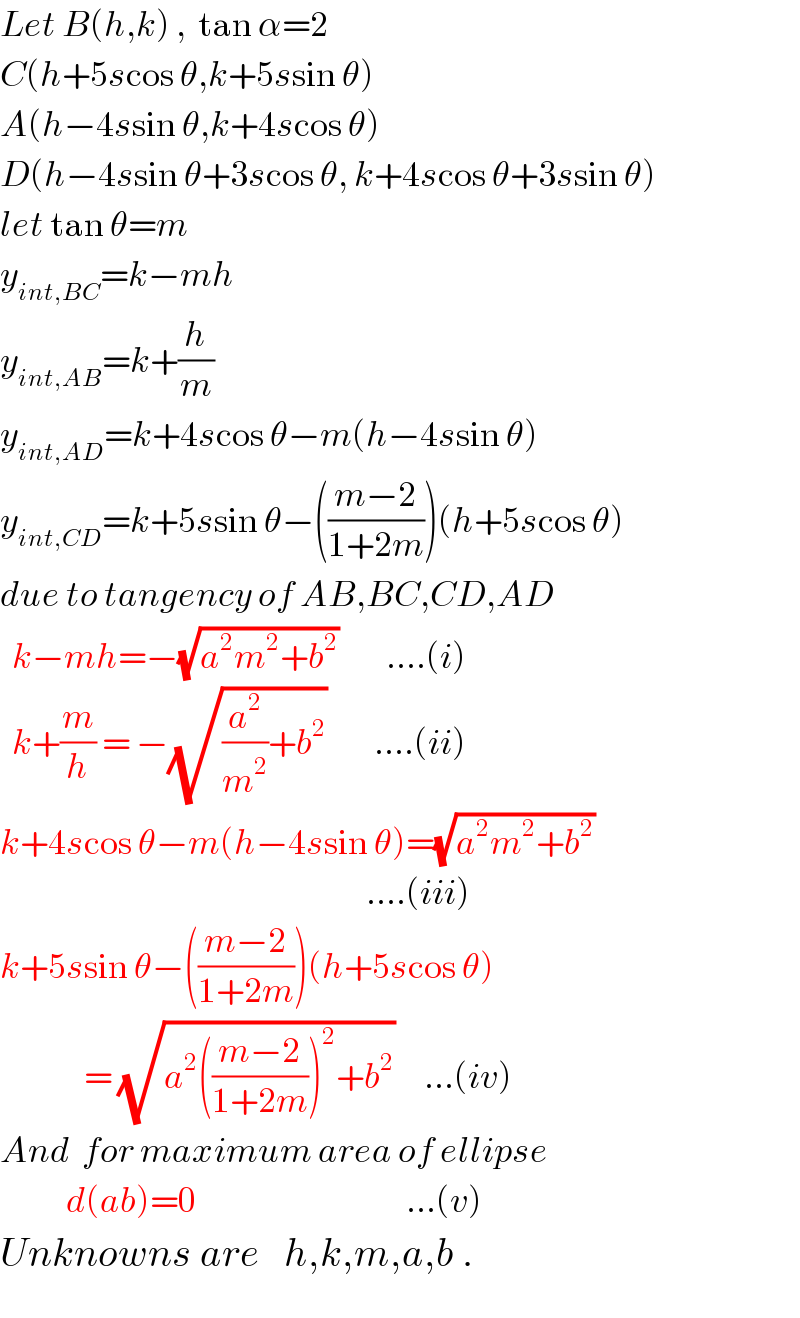
Let B(h,k) , tan α=2 C(h+5scos θ,k+5ssin θ) A(h−4ssin θ,k+4scos θ) D(h−4ssin θ+3scos θ, k+4scos θ+3ssin θ) let tan θ=m y_(int,BC) =k−mh y_(int,AB) =k+(h/m) y_(int,AD) =k+4scos θ−m(h−4ssin θ) y_(int,CD) =k+5ssin θ−(((m−2)/(1+2m)))(h+5scos θ) due to tangency of AB,BC,CD,AD k−mh=−(√(a^2 m^2 +b^2 )) ....(i) k+(m/h) = −(√((a^2 /m^2 )+b^2 )) ....(ii) k+4scos θ−m(h−4ssin θ)=(√(a^2 m^2 +b^2 )) ....(iii) k+5ssin θ−(((m−2)/(1+2m)))(h+5scos θ) = (√(a^2 (((m−2)/(1+2m)))^2 +b^2 )) ...(iv) And for maximum area of ellipse d(ab)=0 ...(v) Unknowns are h,k,m,a,b .

$${Let}\:{B}\left({h},{k}\right)\:,\:\:\mathrm{tan}\:\alpha=\mathrm{2} \\ $$$${C}\left({h}+\mathrm{5}{s}\mathrm{cos}\:\theta,{k}+\mathrm{5}{s}\mathrm{sin}\:\theta\right) \\ $$$${A}\left({h}−\mathrm{4}{s}\mathrm{sin}\:\theta,{k}+\mathrm{4}{s}\mathrm{cos}\:\theta\right) \\ $$$${D}\left({h}−\mathrm{4}{s}\mathrm{sin}\:\theta+\mathrm{3}{s}\mathrm{cos}\:\theta,\:{k}+\mathrm{4}{s}\mathrm{cos}\:\theta+\mathrm{3}{s}\mathrm{sin}\:\theta\right) \\ $$$${let}\:\mathrm{tan}\:\theta={m} \\ $$$${y}_{{int},{BC}} ={k}−{mh} \\ $$$${y}_{{int},{AB}} ={k}+\frac{{h}}{{m}} \\ $$$${y}_{{int},{AD}} ={k}+\mathrm{4}{s}\mathrm{cos}\:\theta−{m}\left({h}−\mathrm{4}{s}\mathrm{sin}\:\theta\right) \\ $$$${y}_{{int},{CD}} ={k}+\mathrm{5}{s}\mathrm{sin}\:\theta−\left(\frac{{m}−\mathrm{2}}{\mathrm{1}+\mathrm{2}{m}}\right)\left({h}+\mathrm{5}{s}\mathrm{cos}\:\theta\right) \\ $$$${due}\:{to}\:{tangency}\:{of}\:{AB},{BC},{CD},{AD} \\ $$$$\:\:{k}−{mh}=−\sqrt{{a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\:\:\:\:\:\:\:....\left({i}\right) \\ $$$$\:\:{k}+\frac{{m}}{{h}}\:=\:−\sqrt{\frac{{a}^{\mathrm{2}} }{{m}^{\mathrm{2}} }+{b}^{\mathrm{2}} }\:\:\:\:\:\:\:\:....\left({ii}\right) \\ $$$${k}+\mathrm{4}{s}\mathrm{cos}\:\theta−{m}\left({h}−\mathrm{4}{s}\mathrm{sin}\:\theta\right)=\sqrt{{a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:....\left({iii}\right) \\ $$$${k}+\mathrm{5}{s}\mathrm{sin}\:\theta−\left(\frac{{m}−\mathrm{2}}{\mathrm{1}+\mathrm{2}{m}}\right)\left({h}+\mathrm{5}{s}\mathrm{cos}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\sqrt{{a}^{\mathrm{2}} \left(\frac{{m}−\mathrm{2}}{\mathrm{1}+\mathrm{2}{m}}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\:\:\:\:...\left({iv}\right) \\ $$$${And}\:\:{for}\:{maximum}\:{area}\:{of}\:{ellipse} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{d}\left({ab}\right)=\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...\left({v}\right) \\ $$$${Unknowns}\:{are}\:\:\:{h},{k},{m},{a},{b}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com