Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 53689 by ajfour last updated on 25/Jan/19

Commented by ajfour last updated on 25/Jan/19

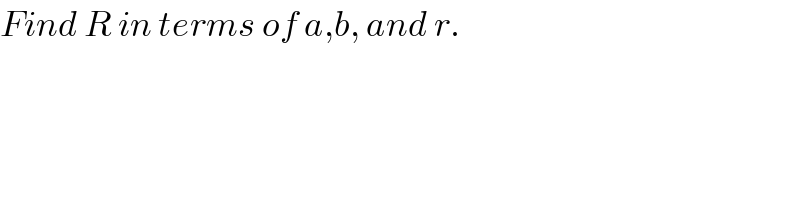
Find R in terms of a,b, and r.

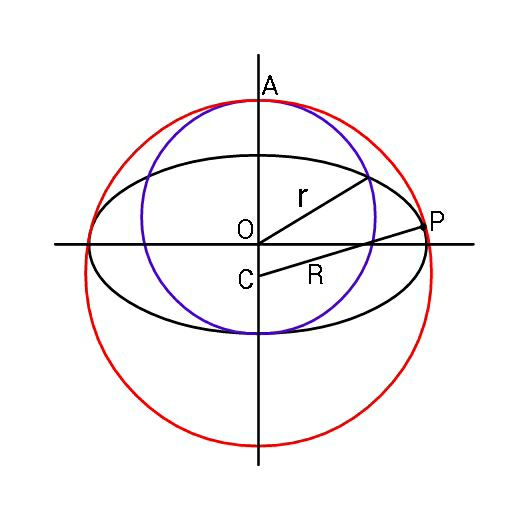
$${Find}\:{R}\:{in}\:{terms}\:{of}\:{a},{b},\:{and}\:{r}. \\ $$

Answered by mr W last updated on 25/Jan/19

A(0, 2r−b) C(0, −k) k=R+b−2r⇒R=k+2r−b eqn. of big circle: x^2 +(y+k)^2 =R^2 (x^2 /a^2 )+(y^2 /b^2 )=1 ((R^2 −(y+k)^2 )/a^2 )+(y^2 /b^2 )=1 b^2 R^2 −b^2 y^2 −b^2 k^2 −2kb^2 y+a^2 y^2 =a^2 b^2 (a^2 −b^2 )y^2 −2kb^2 y+b^2 (R^2 −a^2 −k^2 )=0 Δ=4k^2 b^4 −4(a^2 −b^2 )b^2 (R^2 −a^2 −k^2 )=0 k^2 b^2 −(a^2 −b^2 )(R^2 −a^2 −k^2 )=0 k^2 b^2 −(a^2 −b^2 )[(k+2r−b)^2 −a^2 −k^2 ]=0 ⇒b^2 k^2 −2(a^2 −b^2 )(2r−b)k−(a^2 −b^2 )(2r−b−a)(2r−b+a)=0 ⇒k=(((a^2 −b^2 )(2r−b)±(√((a^2 −b^2 )[(a^2 −b^2 )(2r−b)^2 +b^2 (2r−b−a)(2r−b+a)])))/b^2 ) ⇒k=(((a^2 −b^2 )(2r−b)±2a(√((a^2 −b^2 )(r−b)r)))/b^2 ) ⇒R=2r−b+(((a^2 −b^2 )(2r−b)±2a(√((a^2 −b^2 )(r−b)r)))/b^2 ) ⇒R=((a^2 (2r−b)±2a(√((a^2 −b^2 )(r−b)r)))/b^2 )

$${A}\left(\mathrm{0},\:\mathrm{2}{r}−{b}\right) \\ $$$${C}\left(\mathrm{0},\:−{k}\right) \\ $$$${k}={R}+{b}−\mathrm{2}{r}\Rightarrow{R}={k}+\mathrm{2}{r}−{b} \\ $$$$ \\ $$$${eqn}.\:{of}\:{big}\:{circle}: \\ $$$${x}^{\mathrm{2}} +\left({y}+{k}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{{R}^{\mathrm{2}} −\left({y}+{k}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${b}^{\mathrm{2}} {R}^{\mathrm{2}} −{b}^{\mathrm{2}} {y}^{\mathrm{2}} −{b}^{\mathrm{2}} {k}^{\mathrm{2}} −\mathrm{2}{kb}^{\mathrm{2}} {y}+{a}^{\mathrm{2}} {y}^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){y}^{\mathrm{2}} −\mathrm{2}{kb}^{\mathrm{2}} {y}+{b}^{\mathrm{2}} \left({R}^{\mathrm{2}} −{a}^{\mathrm{2}} −{k}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Delta=\mathrm{4}{k}^{\mathrm{2}} {b}^{\mathrm{4}} −\mathrm{4}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){b}^{\mathrm{2}} \left({R}^{\mathrm{2}} −{a}^{\mathrm{2}} −{k}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${k}^{\mathrm{2}} {b}^{\mathrm{2}} −\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({R}^{\mathrm{2}} −{a}^{\mathrm{2}} −{k}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${k}^{\mathrm{2}} {b}^{\mathrm{2}} −\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left[\left({k}+\mathrm{2}{r}−{b}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} −{k}^{\mathrm{2}} \right]=\mathrm{0} \\ $$$$\Rightarrow{b}^{\mathrm{2}} {k}^{\mathrm{2}} −\mathrm{2}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left(\mathrm{2}{r}−{b}\right){k}−\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left(\mathrm{2}{r}−{b}−{a}\right)\left(\mathrm{2}{r}−{b}+{a}\right)=\mathrm{0} \\ $$$$\Rightarrow{k}=\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left(\mathrm{2}{r}−{b}\right)\pm\sqrt{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left[\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left(\mathrm{2}{r}−{b}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} \left(\mathrm{2}{r}−{b}−{a}\right)\left(\mathrm{2}{r}−{b}+{a}\right)\right]}}{{b}^{\mathrm{2}} } \\ $$$$\Rightarrow{k}=\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left(\mathrm{2}{r}−{b}\right)\pm\mathrm{2}{a}\sqrt{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({r}−{b}\right){r}}}{{b}^{\mathrm{2}} } \\ $$$$\Rightarrow{R}=\mathrm{2}{r}−{b}+\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left(\mathrm{2}{r}−{b}\right)\pm\mathrm{2}{a}\sqrt{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({r}−{b}\right){r}}}{{b}^{\mathrm{2}} } \\ $$$$\Rightarrow{R}=\frac{{a}^{\mathrm{2}} \left(\mathrm{2}{r}−{b}\right)\pm\mathrm{2}{a}\sqrt{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({r}−{b}\right){r}}}{{b}^{\mathrm{2}} } \\ $$

Commented by ajfour last updated on 25/Jan/19

thanks, Sir. How to choose among the signs?

$${thanks},\:{Sir}.\:{How}\:{to}\:{choose}\:{among}\:{the}\:{signs}? \\ $$

Commented by mr W last updated on 25/Jan/19

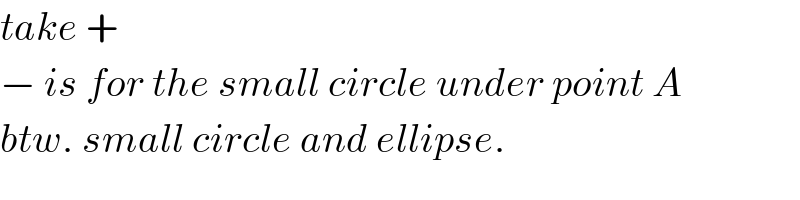
take + − is for the small circle under point A btw. small circle and ellipse.

$${take}\:+ \\ $$$$−\:{is}\:{for}\:{the}\:{small}\:{circle}\:{under}\:{point}\:{A} \\ $$$${btw}.\:{small}\:{circle}\:{and}\:{ellipse}. \\ $$

Commented by ajfour last updated on 25/Jan/19

Yes sir, understood, as i attempted.

$${Yes}\:{sir},\:{understood},\:{as}\:{i}\:{attempted}. \\ $$

Answered by ajfour last updated on 25/Jan/19

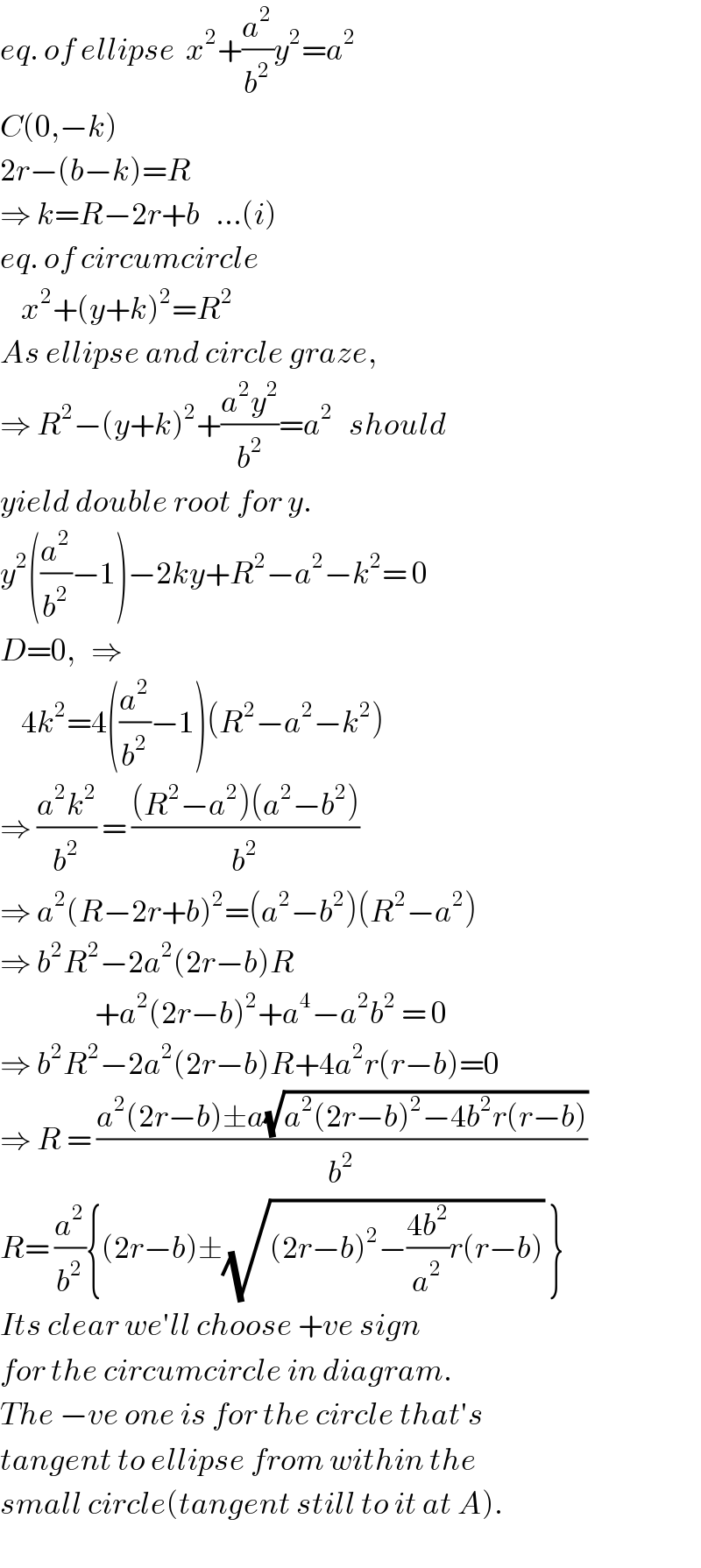
eq. of ellipse x^2 +(a^2 /b^2 )y^2 =a^2 C(0,−k) 2r−(b−k)=R ⇒ k=R−2r+b ...(i) eq. of circumcircle x^2 +(y+k)^2 =R^2 As ellipse and circle graze, ⇒ R^2 −(y+k)^2 +((a^2 y^2 )/b^2 )=a^2 should yield double root for y. y^2 ((a^2 /b^2 )−1)−2ky+R^2 −a^2 −k^2 = 0 D=0, ⇒ 4k^2 =4((a^2 /b^2 )−1)(R^2 −a^2 −k^2 ) ⇒ ((a^2 k^2 )/b^2 ) = (((R^2 −a^2 )(a^2 −b^2 ))/b^2 ) ⇒ a^2 (R−2r+b)^2 =(a^2 −b^2 )(R^2 −a^2 ) ⇒ b^2 R^2 −2a^2 (2r−b)R +a^2 (2r−b)^2 +a^4 −a^2 b^2 = 0 ⇒ b^2 R^2 −2a^2 (2r−b)R+4a^2 r(r−b)=0 ⇒ R = ((a^2 (2r−b)±a(√(a^2 (2r−b)^2 −4b^2 r(r−b))))/b^2 ) R= (a^2 /b^2 ){(2r−b)±(√((2r−b)^2 −((4b^2 )/a^2 )r(r−b))) } Its clear we′ll choose +ve sign for the circumcircle in diagram. The −ve one is for the circle that′s tangent to ellipse from within the small circle(tangent still to it at A).

$${eq}.\:{of}\:{ellipse}\:\:{x}^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$${C}\left(\mathrm{0},−{k}\right) \\ $$$$\mathrm{2}{r}−\left({b}−{k}\right)={R} \\ $$$$\Rightarrow\:{k}={R}−\mathrm{2}{r}+{b}\:\:\:...\left({i}\right) \\ $$$${eq}.\:{of}\:{circumcircle} \\ $$$$\:\:\:\:{x}^{\mathrm{2}} +\left({y}+{k}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${As}\:{ellipse}\:{and}\:{circle}\:{graze}, \\ $$$$\Rightarrow\:{R}^{\mathrm{2}} −\left({y}+{k}\right)^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} {y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }={a}^{\mathrm{2}} \:\:\:{should} \\ $$$${yield}\:{double}\:{root}\:{for}\:{y}. \\ $$$${y}^{\mathrm{2}} \left(\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\mathrm{1}\right)−\mathrm{2}{ky}+{R}^{\mathrm{2}} −{a}^{\mathrm{2}} −{k}^{\mathrm{2}} =\:\mathrm{0} \\ $$$${D}=\mathrm{0},\:\:\:\Rightarrow \\ $$$$\:\:\:\:\mathrm{4}{k}^{\mathrm{2}} =\mathrm{4}\left(\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\mathrm{1}\right)\left({R}^{\mathrm{2}} −{a}^{\mathrm{2}} −{k}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\frac{{a}^{\mathrm{2}} {k}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:=\:\frac{\left({R}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{{b}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} \left({R}−\mathrm{2}{r}+{b}\right)^{\mathrm{2}} =\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({R}^{\mathrm{2}} −{a}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:{b}^{\mathrm{2}} {R}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} \left(\mathrm{2}{r}−{b}\right){R} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{a}^{\mathrm{2}} \left(\mathrm{2}{r}−{b}\right)^{\mathrm{2}} +{a}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\Rightarrow\:{b}^{\mathrm{2}} {R}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} \left(\mathrm{2}{r}−{b}\right){R}+\mathrm{4}{a}^{\mathrm{2}} {r}\left({r}−{b}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{R}\:=\:\frac{{a}^{\mathrm{2}} \left(\mathrm{2}{r}−{b}\right)\pm{a}\sqrt{{a}^{\mathrm{2}} \left(\mathrm{2}{r}−{b}\right)^{\mathrm{2}} −\mathrm{4}{b}^{\mathrm{2}} {r}\left({r}−{b}\right)}}{{b}^{\mathrm{2}} } \\ $$$${R}=\:\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\left\{\left(\mathrm{2}{r}−{b}\right)\pm\sqrt{\left(\mathrm{2}{r}−{b}\right)^{\mathrm{2}} −\frac{\mathrm{4}{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }{r}\left({r}−{b}\right)}\:\right\} \\ $$$${Its}\:{clear}\:{we}'{ll}\:{choose}\:+{ve}\:{sign} \\ $$$${for}\:{the}\:{circumcircle}\:{in}\:{diagram}. \\ $$$${The}\:−{ve}\:{one}\:{is}\:{for}\:{the}\:{circle}\:{that}'{s} \\ $$$${tangent}\:{to}\:{ellipse}\:{from}\:{within}\:{the} \\ $$$${small}\:{circle}\left({tangent}\:{still}\:{to}\:{it}\:{at}\:{A}\right). \\ $$

Commented by mr W last updated on 25/Jan/19

very fine sir!

$${very}\:{fine}\:{sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com