
Question Number 53664 by ajfour last updated on 24/Jan/19
Commented by ajfour last updated on 24/Jan/19

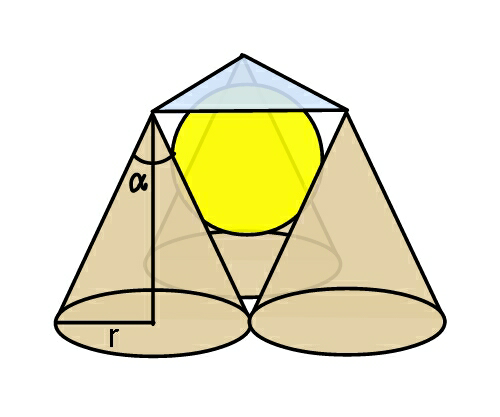
$${The}\:{bases}\:{of}\:{the}\:{cones}\:{touch}\:{each} \\ $$$${other}\:{pairwise}.\:{Find}\:{the}\:{radius}\:{of} \\ $$$${the}\:{sphere}\:{tangent}\:{to}\:{all}\:{the}\:{three} \\ $$$${cones}\:{and}\:{to}\:{the}\:{plane}\:{passing} \\ $$$${through}\:{their}\:{vertices}.\:\left({semi}-{vertical}\right. \\ $$$$\left.{angles}\:{of}\:{the}\:{cones}\:{is}\:\alpha/\mathrm{2}\right) \\ $$
Answered by mr W last updated on 24/Jan/19
Commented by mr W last updated on 24/Jan/19
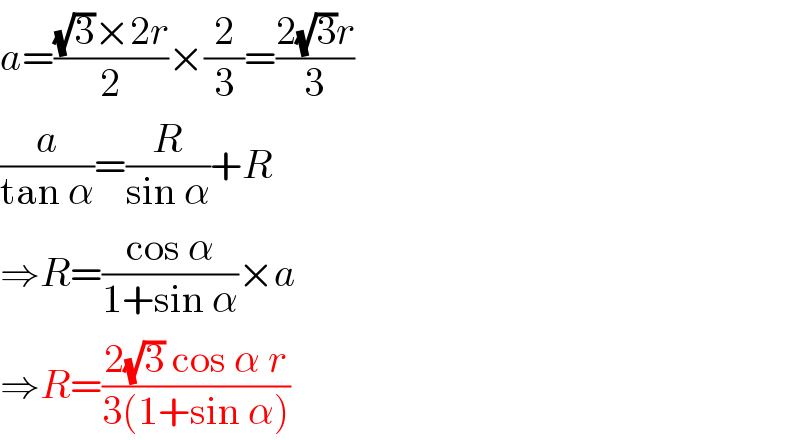
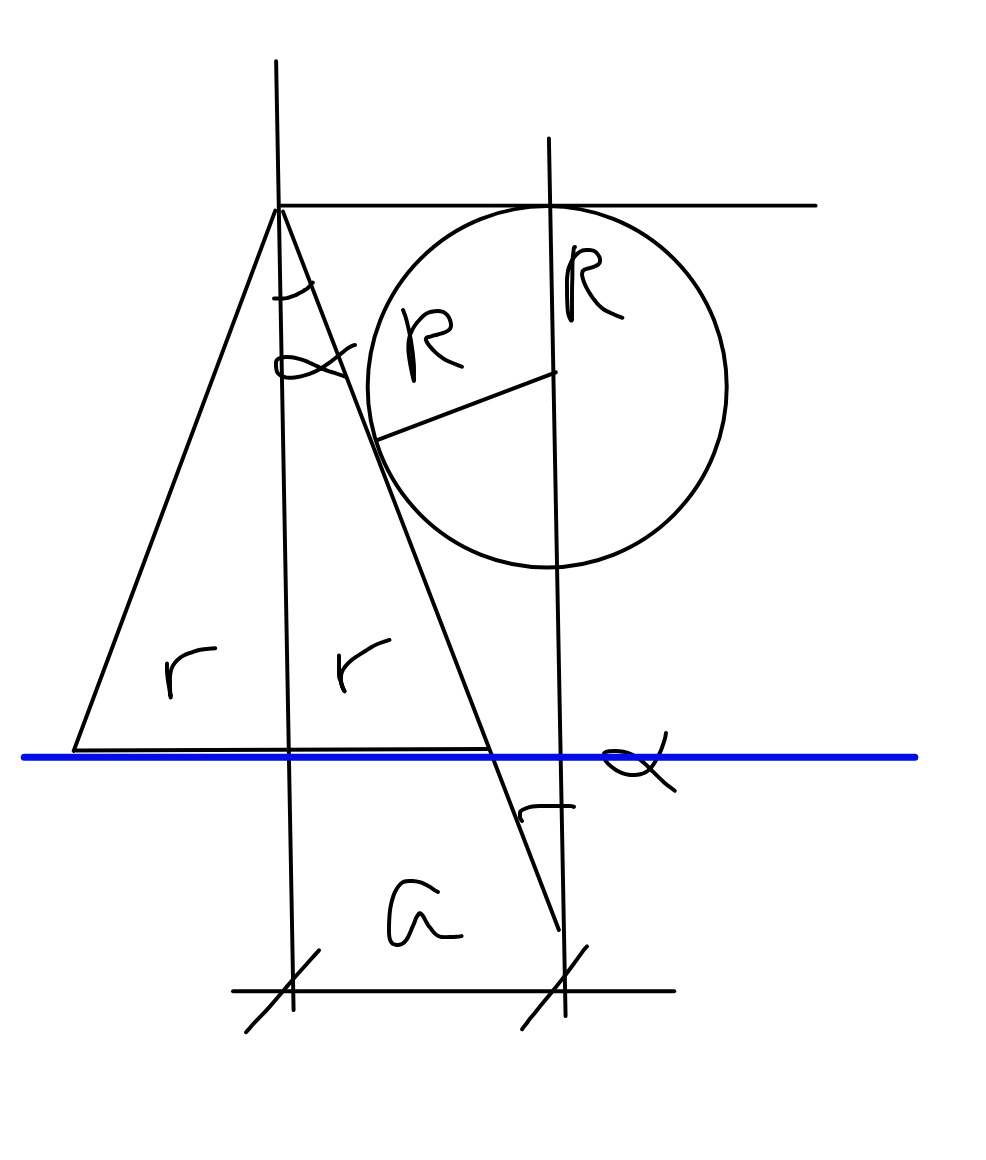
$${a}=\frac{\sqrt{\mathrm{3}}×\mathrm{2}{r}}{\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{2}\sqrt{\mathrm{3}}{r}}{\mathrm{3}} \\ $$$$\frac{{a}}{\mathrm{tan}\:\alpha}=\frac{{R}}{\mathrm{sin}\:\alpha}+{R} \\ $$$$\Rightarrow{R}=\frac{\mathrm{cos}\:\alpha}{\mathrm{1}+\mathrm{sin}\:\alpha}×{a} \\ $$$$\Rightarrow{R}=\frac{\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{cos}\:\alpha\:{r}}{\mathrm{3}\left(\mathrm{1}+\mathrm{sin}\:\alpha\right)} \\ $$
Commented by ajfour last updated on 25/Jan/19
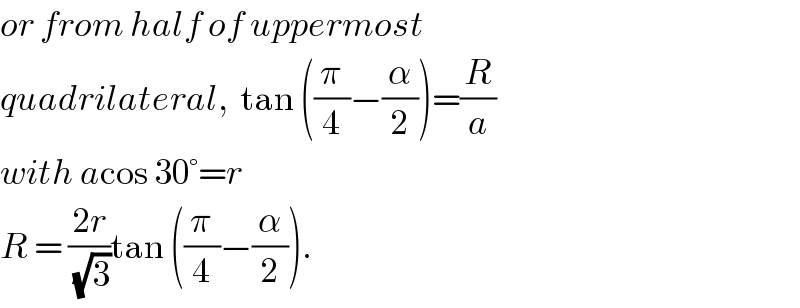
$${or}\:{from}\:{half}\:{of}\:{uppermost}\: \\ $$$${quadrilateral},\:\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\mathrm{2}}\right)=\frac{{R}}{{a}} \\ $$$${with}\:{a}\mathrm{cos}\:\mathrm{30}°={r} \\ $$$${R}\:=\:\frac{\mathrm{2}{r}}{\sqrt{\mathrm{3}}}\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\mathrm{2}}\right). \\ $$
