Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 53492 by ajfour last updated on 22/Jan/19

Commented by ajfour last updated on 22/Jan/19

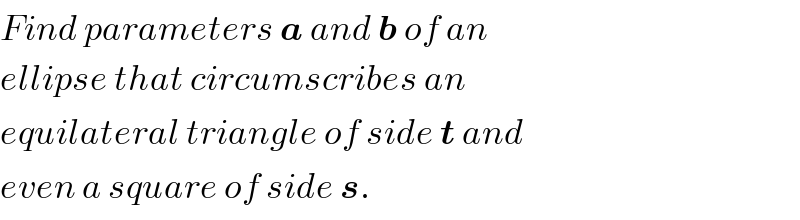
Find parameters a and b of an ellipse that circumscribes an equilateral triangle of side t and even a square of side s.

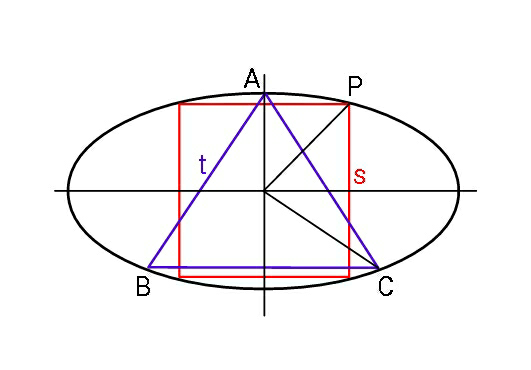
$${Find}\:{parameters}\:\boldsymbol{{a}}\:{and}\:\boldsymbol{{b}}\:{of}\:{an} \\ $$$${ellipse}\:{that}\:{circumscribes}\:{an} \\ $$$${equilateral}\:{triangle}\:{of}\:{side}\:\boldsymbol{{t}}\:{and} \\ $$$${even}\:{a}\:{square}\:{of}\:{side}\:\boldsymbol{{s}}. \\ $$

Answered by mr W last updated on 22/Jan/19

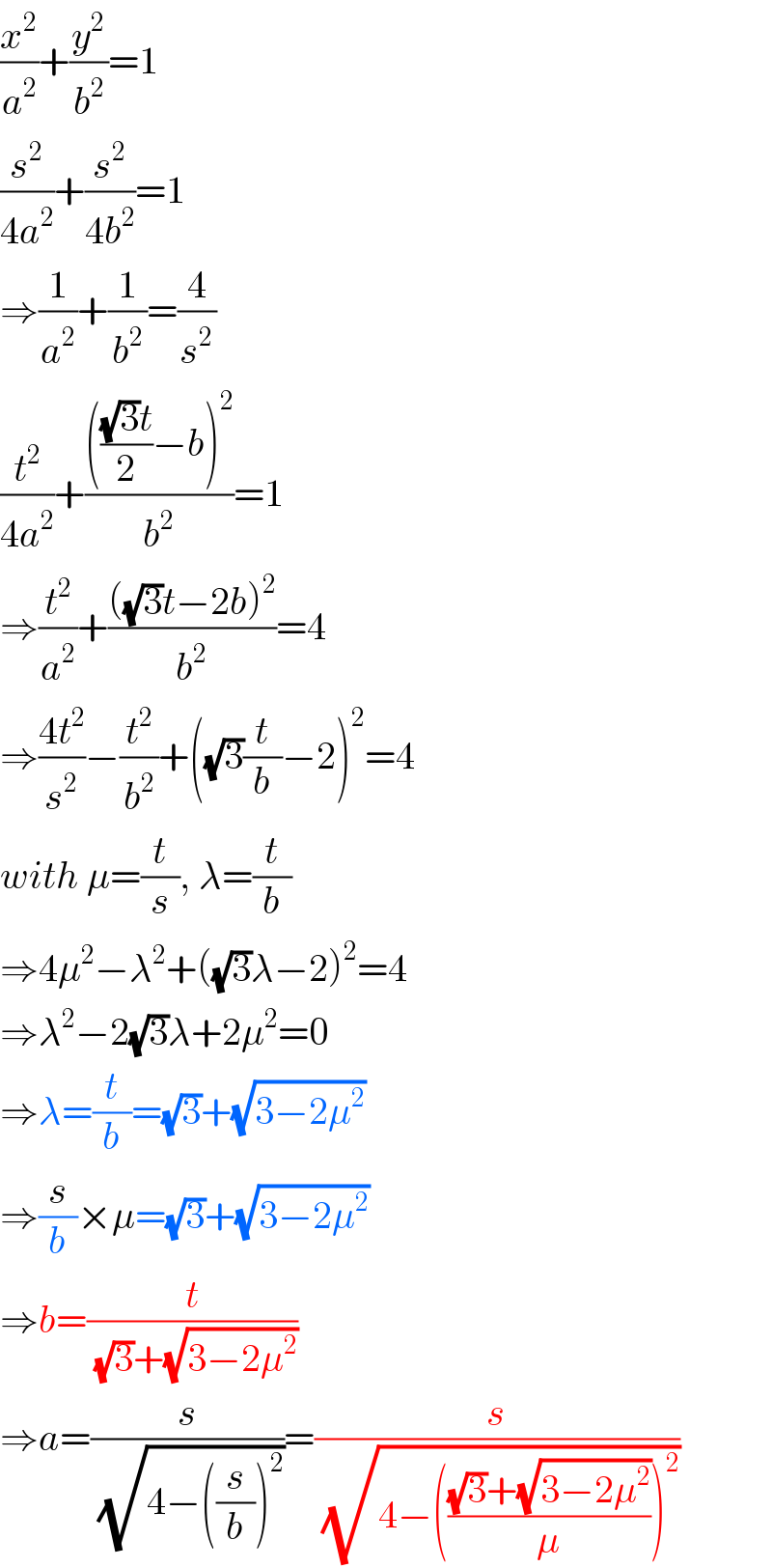
(x^2 /a^2 )+(y^2 /b^2 )=1 (s^2 /(4a^2 ))+(s^2 /(4b^2 ))=1 ⇒(1/a^2 )+(1/b^2 )=(4/s^2 ) (t^2 /(4a^2 ))+((((((√3)t)/2)−b)^2 )/b^2 )=1 ⇒(t^2 /a^2 )+((((√3)t−2b)^2 )/b^2 )=4 ⇒((4t^2 )/s^2 )−(t^2 /b^2 )+((√3)(t/b)−2)^2 =4 with μ=(t/s), λ=(t/b) ⇒4μ^2 −λ^2 +((√3)λ−2)^2 =4 ⇒λ^2 −2(√3)λ+2μ^2 =0 ⇒λ=(t/b)=(√3)+(√(3−2μ^2 )) ⇒(s/b)×μ=(√3)+(√(3−2μ^2 )) ⇒b=(t/((√3)+(√(3−2μ^2 )))) ⇒a=(s/(√(4−((s/b))^2 )))=(s/(√(4−((((√3)+(√(3−2μ^2 )))/μ))^2 )))

$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{{s}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }+\frac{{s}^{\mathrm{2}} }{\mathrm{4}{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }=\frac{\mathrm{4}}{{s}^{\mathrm{2}} } \\ $$$$\frac{{t}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }+\frac{\left(\frac{\sqrt{\mathrm{3}}{t}}{\mathrm{2}}−{b}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow\frac{{t}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left(\sqrt{\mathrm{3}}{t}−\mathrm{2}{b}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{4} \\ $$$$\Rightarrow\frac{\mathrm{4}{t}^{\mathrm{2}} }{{s}^{\mathrm{2}} }−\frac{{t}^{\mathrm{2}} }{{b}^{\mathrm{2}} }+\left(\sqrt{\mathrm{3}}\frac{{t}}{{b}}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{4} \\ $$$${with}\:\mu=\frac{{t}}{{s}},\:\lambda=\frac{{t}}{{b}} \\ $$$$\Rightarrow\mathrm{4}\mu^{\mathrm{2}} −\lambda^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}\lambda−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{4} \\ $$$$\Rightarrow\lambda^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}\lambda+\mathrm{2}\mu^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\lambda=\frac{{t}}{{b}}=\sqrt{\mathrm{3}}+\sqrt{\mathrm{3}−\mathrm{2}\mu^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{s}}{{b}}×\mu=\sqrt{\mathrm{3}}+\sqrt{\mathrm{3}−\mathrm{2}\mu^{\mathrm{2}} } \\ $$$$\Rightarrow{b}=\frac{{t}}{\sqrt{\mathrm{3}}+\sqrt{\mathrm{3}−\mathrm{2}\mu^{\mathrm{2}} }} \\ $$$$\Rightarrow{a}=\frac{{s}}{\sqrt{\mathrm{4}−\left(\frac{{s}}{{b}}\right)^{\mathrm{2}} }}=\frac{{s}}{\sqrt{\mathrm{4}−\left(\frac{\sqrt{\mathrm{3}}+\sqrt{\mathrm{3}−\mathrm{2}\mu^{\mathrm{2}} }}{\mu}\right)^{\mathrm{2}} }} \\ $$

Commented by ajfour last updated on 23/Jan/19

Its shorter than the parametric way, thanks Sir.

$${Its}\:{shorter}\:{than}\:{the}\:{parametric}\:{way}, \\ $$$${thanks}\:{Sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com