
Question Number 53447 by rajeshghorai130@gmail.com last updated on 22/Jan/19
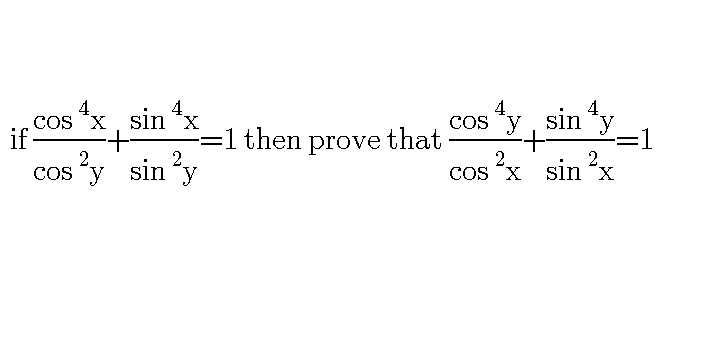
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jan/19
![a=sin^2 x b=sin^2 y (((1−a)^2 )/(1−b))+(a^2 /b)=1 b−2ab+a^2 b+a^2 −a^2 b=b−b^2 b−2ab+a^2 −b+b^2 =0 (a−b)^2 =0 a=b sin^2 x=sin^2 y [so x=y] ((cos^4 y)/(cos^2 x))+((sin^4 y)/(sin^2 x)) =((cos^4 x)/(cos^2 x))+((sin^4 x)/(sin^2 x)) =cos^2 x+sin^2 x =1 proved](Q53448.png)
$${a}={sin}^{\mathrm{2}} {x} \\ $$$${b}={sin}^{\mathrm{2}} {y} \\ $$$$\frac{\left(\mathrm{1}−{a}\right)^{\mathrm{2}} }{\mathrm{1}−{b}}+\frac{{a}^{\mathrm{2}} }{{b}}=\mathrm{1} \\ $$$${b}−\mathrm{2}{ab}+{a}^{\mathrm{2}} {b}+{a}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}={b}−{b}^{\mathrm{2}} \\ $$$${b}−\mathrm{2}{ab}+{a}^{\mathrm{2}} −{b}+{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({a}−{b}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${a}={b} \\ $$$${sin}^{\mathrm{2}} {x}={sin}^{\mathrm{2}} {y}\:\:\:\left[{so}\:{x}={y}\right] \\ $$$$ \\ $$$$\frac{{cos}^{\mathrm{4}} {y}}{{cos}^{\mathrm{2}} {x}}+\frac{{sin}^{\mathrm{4}} {y}}{{sin}^{\mathrm{2}} {x}} \\ $$$$=\frac{{cos}^{\mathrm{4}} {x}}{{cos}^{\mathrm{2}} {x}}+\frac{{sin}^{\mathrm{4}} {x}}{{sin}^{\mathrm{2}} {x}} \\ $$$$={cos}^{\mathrm{2}} {x}+{sin}^{\mathrm{2}} {x} \\ $$$$=\mathrm{1}\:{proved} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
