
Question Number 53276 by ajfour last updated on 19/Jan/19

Commented by ajfour last updated on 19/Jan/19
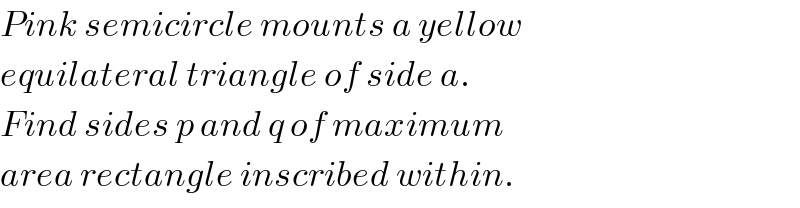
$${Pink}\:{semicircle}\:{mounts}\:{a}\:{yellow}\: \\ $$$${equilateral}\:{triangle}\:{of}\:{side}\:{a}. \\ $$$${Find}\:{sides}\:{p}\:{and}\:{q}\:{of}\:{maximum} \\ $$$${area}\:{rectangle}\:{inscribed}\:{within}. \\ $$
Answered by mr W last updated on 20/Jan/19
![p=(1/2)(√(a^2 −q^2 ))+(((√3)a)/2)(1−(q/a)) A=pq=(q/2)[(√(a^2 −q^z ))+(√3)a(1−(q/a))] A=(a^2 /2)[(√(1−λ^2 ))+(√3)(1−λ)]λ with λ=(q/a) ((d(((2A)/a^2 )))/dλ)=0 (√(1−λ^2 ))+(√3)(1−λ)+λ[−(λ/(√(1−λ^2 )))−(√3)]=0 ⇒(√(3(1−λ^2 )))(1−2λ)=2λ^2 −1 ⇒λ=0.6006 ⇒A_(max) =0.4478a^2](Q53299.png)
$${p}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −{q}^{\mathrm{2}} }+\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}\left(\mathrm{1}−\frac{{q}}{{a}}\right) \\ $$$${A}={pq}=\frac{{q}}{\mathrm{2}}\left[\sqrt{{a}^{\mathrm{2}} −{q}^{{z}} }+\sqrt{\mathrm{3}}{a}\left(\mathrm{1}−\frac{{q}}{{a}}\right)\right] \\ $$$${A}=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left[\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }+\sqrt{\mathrm{3}}\left(\mathrm{1}−\lambda\right)\right]\lambda\:{with}\:\lambda=\frac{{q}}{{a}} \\ $$$$\frac{{d}\left(\frac{\mathrm{2}{A}}{{a}^{\mathrm{2}} }\right)}{{d}\lambda}=\mathrm{0} \\ $$$$\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }+\sqrt{\mathrm{3}}\left(\mathrm{1}−\lambda\right)+\lambda\left[−\frac{\lambda}{\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}−\sqrt{\mathrm{3}}\right]=\mathrm{0} \\ $$$$\Rightarrow\sqrt{\mathrm{3}\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)}\left(\mathrm{1}−\mathrm{2}\lambda\right)=\mathrm{2}\lambda^{\mathrm{2}} −\mathrm{1} \\ $$$$\Rightarrow\lambda=\mathrm{0}.\mathrm{6006} \\ $$$$\Rightarrow{A}_{{max}} =\mathrm{0}.\mathrm{4478}{a}^{\mathrm{2}} \\ $$
Commented by ajfour last updated on 20/Jan/19
$${Thanks}\:{Sir},\:{really}\:{precise}\:\&\:{excellent}! \\ $$
