
Question Number 53273 by ajfour last updated on 19/Jan/19
Commented by ajfour last updated on 19/Jan/19

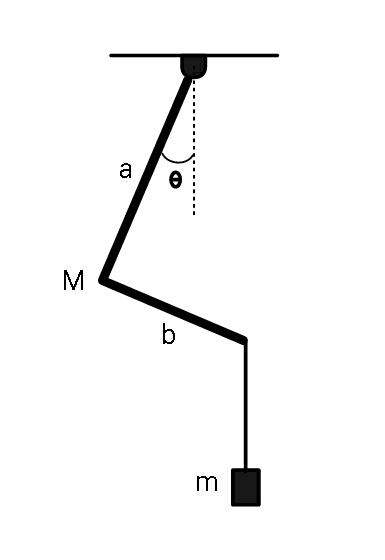
$${If}\:{system}\:{is}\:{in}\:{equilibrium},\:{find}\:\theta. \\ $$$${rod}\:{is}\:{L}\:{shaped}\:{and}\:{uniform}. \\ $$
Answered by mr W last updated on 19/Jan/19
![((aMg)/(a+b))×((a sin θ)/2)+((bMg)/(a+b))×(a sin θ−((b cos θ)/2))+mg(a sin θ−b cos θ)=0 (a/(a+b))×a tan θ+(b/(a+b))×(2a tan θ−b)+((2m)/M)(a tan θ−b)=0 (((a^2 +2ab)/(a+b))+((2ma)/M)) tan θ=(b^2 /(a+b))+((2mb)/M) ⇒θ=tan^(−1) ((b[bM+2(a+b)m])/(a[(a+2b)M+2(a+b)m]))](Q53281.png)
$$\frac{{aMg}}{{a}+{b}}×\frac{{a}\:\mathrm{sin}\:\theta}{\mathrm{2}}+\frac{{bMg}}{{a}+{b}}×\left({a}\:\mathrm{sin}\:\theta−\frac{{b}\:\mathrm{cos}\:\theta}{\mathrm{2}}\right)+{mg}\left({a}\:\mathrm{sin}\:\theta−{b}\:\mathrm{cos}\:\theta\right)=\mathrm{0} \\ $$$$\frac{{a}}{{a}+{b}}×{a}\:\mathrm{tan}\:\theta+\frac{{b}}{{a}+{b}}×\left(\mathrm{2}{a}\:\mathrm{tan}\:\theta−{b}\right)+\frac{\mathrm{2}{m}}{{M}}\left({a}\:\mathrm{tan}\:\theta−{b}\right)=\mathrm{0} \\ $$$$\left(\frac{{a}^{\mathrm{2}} +\mathrm{2}{ab}}{{a}+{b}}+\frac{\mathrm{2}{ma}}{{M}}\right)\:\mathrm{tan}\:\theta=\frac{{b}^{\mathrm{2}} }{{a}+{b}}+\frac{\mathrm{2}{mb}}{{M}} \\ $$$$\Rightarrow\theta=\mathrm{tan}^{−\mathrm{1}} \frac{{b}\left[{bM}+\mathrm{2}\left({a}+{b}\right){m}\right]}{{a}\left[\left({a}+\mathrm{2}{b}\right){M}+\mathrm{2}\left({a}+{b}\right){m}\right]} \\ $$
Commented by ajfour last updated on 20/Jan/19
$${Thank}\:{you}\:{Sir},\:{answer}\:{is}\:{presented} \\ $$$${the}\:{best}\:{way}. \\ $$
