
Question Number 53252 by ajfour last updated on 19/Jan/19
Commented by ajfour last updated on 19/Jan/19
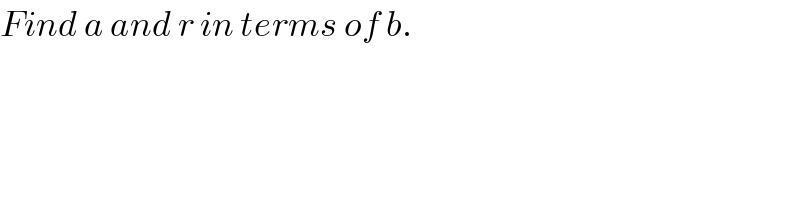
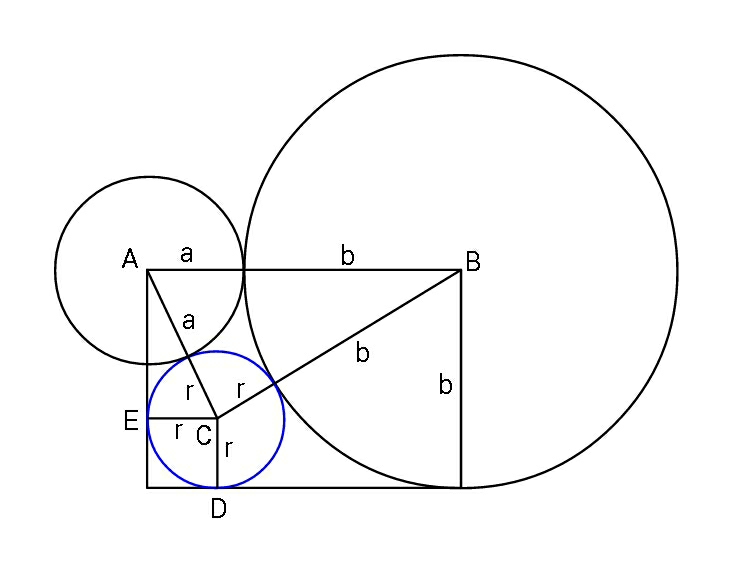
$${Find}\:{a}\:{and}\:{r}\:{in}\:{terms}\:{of}\:{b}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 19/Jan/19
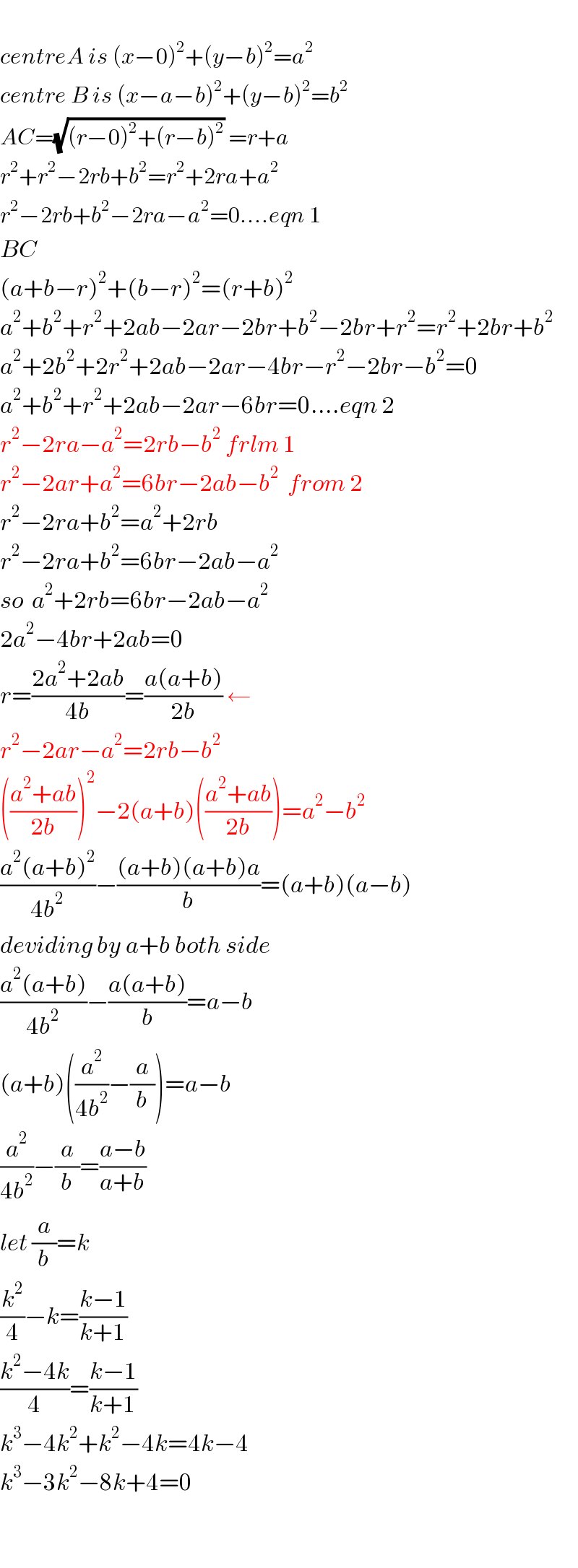
$$ \\ $$$${centreA}\:{is}\:\left({x}−\mathrm{0}\right)^{\mathrm{2}} +\left({y}−{b}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$${centre}\:{B}\:{is}\:\left({x}−{a}−{b}\right)^{\mathrm{2}} +\left({y}−{b}\right)^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$${AC}=\sqrt{\left({r}−\mathrm{0}\right)^{\mathrm{2}} +\left({r}−{b}\right)^{\mathrm{2}} }\:={r}+{a} \\ $$$${r}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{rb}+{b}^{\mathrm{2}} ={r}^{\mathrm{2}} +\mathrm{2}{ra}+{a}^{\mathrm{2}} \\ $$$${r}^{\mathrm{2}} −\mathrm{2}{rb}+{b}^{\mathrm{2}} −\mathrm{2}{ra}−{a}^{\mathrm{2}} =\mathrm{0}....{eqn}\:\mathrm{1} \\ $$$${BC} \\ $$$$\left({a}+{b}−{r}\right)^{\mathrm{2}} +\left({b}−{r}\right)^{\mathrm{2}} =\left({r}+{b}\right)^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{r}^{\mathrm{2}} +\mathrm{2}{ab}−\mathrm{2}{ar}−\mathrm{2}{br}+{b}^{\mathrm{2}} −\mathrm{2}{br}+{r}^{\mathrm{2}} ={r}^{\mathrm{2}} +\mathrm{2}{br}+{b}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} +\mathrm{2}{r}^{\mathrm{2}} +\mathrm{2}{ab}−\mathrm{2}{ar}−\mathrm{4}{br}−{r}^{\mathrm{2}} −\mathrm{2}{br}−{b}^{\mathrm{2}} =\mathrm{0} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{r}^{\mathrm{2}} +\mathrm{2}{ab}−\mathrm{2}{ar}−\mathrm{6}{br}=\mathrm{0}....{eqn}\:\mathrm{2} \\ $$$${r}^{\mathrm{2}} −\mathrm{2}{ra}−{a}^{\mathrm{2}} =\mathrm{2}{rb}−{b}^{\mathrm{2}} \:{frlm}\:\mathrm{1} \\ $$$${r}^{\mathrm{2}} −\mathrm{2}{ar}+{a}^{\mathrm{2}} =\mathrm{6}{br}−\mathrm{2}{ab}−{b}^{\mathrm{2}} \:\:{from}\:\mathrm{2} \\ $$$${r}^{\mathrm{2}} −\mathrm{2}{ra}+{b}^{\mathrm{2}} ={a}^{\mathrm{2}} +\mathrm{2}{rb} \\ $$$${r}^{\mathrm{2}} −\mathrm{2}{ra}+{b}^{\mathrm{2}} =\mathrm{6}{br}−\mathrm{2}{ab}−{a}^{\mathrm{2}} \\ $$$${so}\:\:{a}^{\mathrm{2}} +\mathrm{2}{rb}=\mathrm{6}{br}−\mathrm{2}{ab}−{a}^{\mathrm{2}} \\ $$$$\mathrm{2}{a}^{\mathrm{2}} −\mathrm{4}{br}+\mathrm{2}{ab}=\mathrm{0} \\ $$$${r}=\frac{\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{ab}}{\mathrm{4}{b}}=\frac{{a}\left({a}+{b}\right)}{\mathrm{2}{b}}\:\leftarrow \\ $$$${r}^{\mathrm{2}} −\mathrm{2}{ar}−{a}^{\mathrm{2}} =\mathrm{2}{rb}−{b}^{\mathrm{2}} \\ $$$$\left(\frac{{a}^{\mathrm{2}} +{ab}}{\mathrm{2}{b}}\right)^{\mathrm{2}} −\mathrm{2}\left({a}+{b}\right)\left(\frac{{a}^{\mathrm{2}} +{ab}}{\mathrm{2}{b}}\right)={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$$\frac{{a}^{\mathrm{2}} \left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{4}{b}^{\mathrm{2}} }−\frac{\left({a}+{b}\right)\left({a}+{b}\right){a}}{{b}}=\left({a}+{b}\right)\left({a}−{b}\right) \\ $$$${deviding}\:{by}\:{a}+{b}\:{both}\:{side} \\ $$$$\frac{{a}^{\mathrm{2}} \left({a}+{b}\right)}{\mathrm{4}{b}^{\mathrm{2}} }−\frac{{a}\left({a}+{b}\right)}{{b}}={a}−{b} \\ $$$$\left({a}+{b}\right)\left(\frac{{a}^{\mathrm{2}} }{\mathrm{4}{b}^{\mathrm{2}} }−\frac{{a}}{{b}}\right)={a}−{b} \\ $$$$\frac{{a}^{\mathrm{2}} }{\mathrm{4}{b}^{\mathrm{2}} }−\frac{{a}}{{b}}=\frac{{a}−{b}}{{a}+{b}}\: \\ $$$${let}\:\frac{{a}}{{b}}={k} \\ $$$$\frac{{k}^{\mathrm{2}} }{\mathrm{4}}−{k}=\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}} \\ $$$$\frac{{k}^{\mathrm{2}} −\mathrm{4}{k}}{\mathrm{4}}=\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}} \\ $$$${k}^{\mathrm{3}} −\mathrm{4}{k}^{\mathrm{2}} +{k}^{\mathrm{2}} −\mathrm{4}{k}=\mathrm{4}{k}−\mathrm{4} \\ $$$${k}^{\mathrm{3}} −\mathrm{3}{k}^{\mathrm{2}} −\mathrm{8}{k}+\mathrm{4}=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Jan/19
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Jan/19
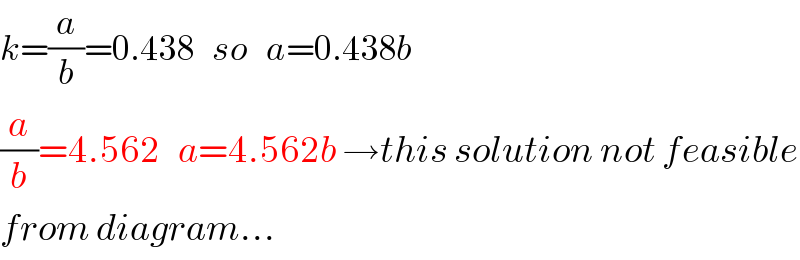
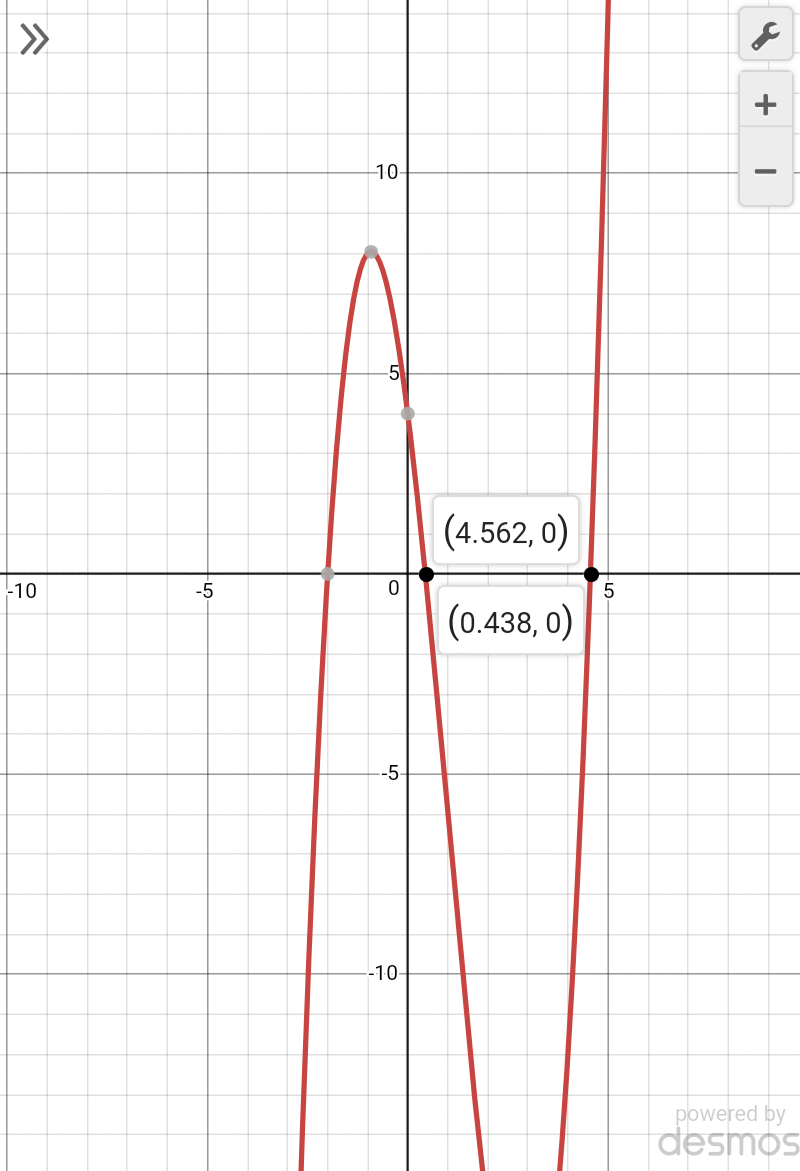
$${k}=\frac{{a}}{{b}}=\mathrm{0}.\mathrm{438}\:\:\:{so}\:\:\:{a}=\mathrm{0}.\mathrm{438}{b} \\ $$$$\frac{{a}}{{b}}=\mathrm{4}.\mathrm{562}\:\:\:{a}=\mathrm{4}.\mathrm{562}{b}\:\rightarrow{this}\:{solution}\:{not}\:{feasible} \\ $$$${from}\:{diagram}... \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Jan/19
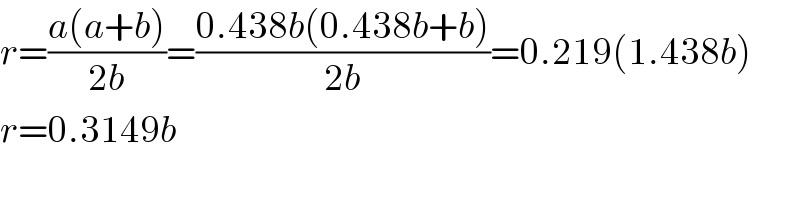
$${r}=\frac{{a}\left({a}+{b}\right)}{\mathrm{2}{b}}=\frac{\mathrm{0}.\mathrm{438}{b}\left(\mathrm{0}.\mathrm{438}{b}+{b}\right)}{\mathrm{2}{b}}=\mathrm{0}.\mathrm{219}\left(\mathrm{1}.\mathrm{438}{b}\right) \\ $$$${r}=\mathrm{0}.\mathrm{3149}{b} \\ $$
Answered by ajfour last updated on 19/Jan/19
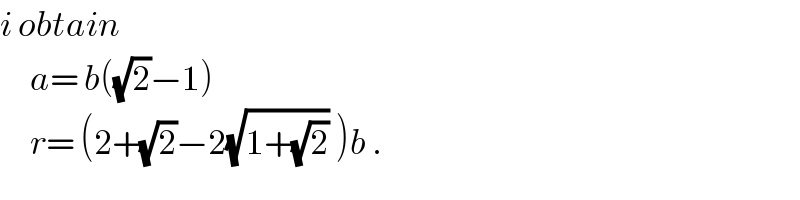
$${i}\:{obtain} \\ $$$$\:\:\:\:\:{a}=\:{b}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:{r}=\:\left(\mathrm{2}+\sqrt{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{1}+\sqrt{\mathrm{2}}}\:\right){b}\:. \\ $$
Answered by ajfour last updated on 19/Jan/19
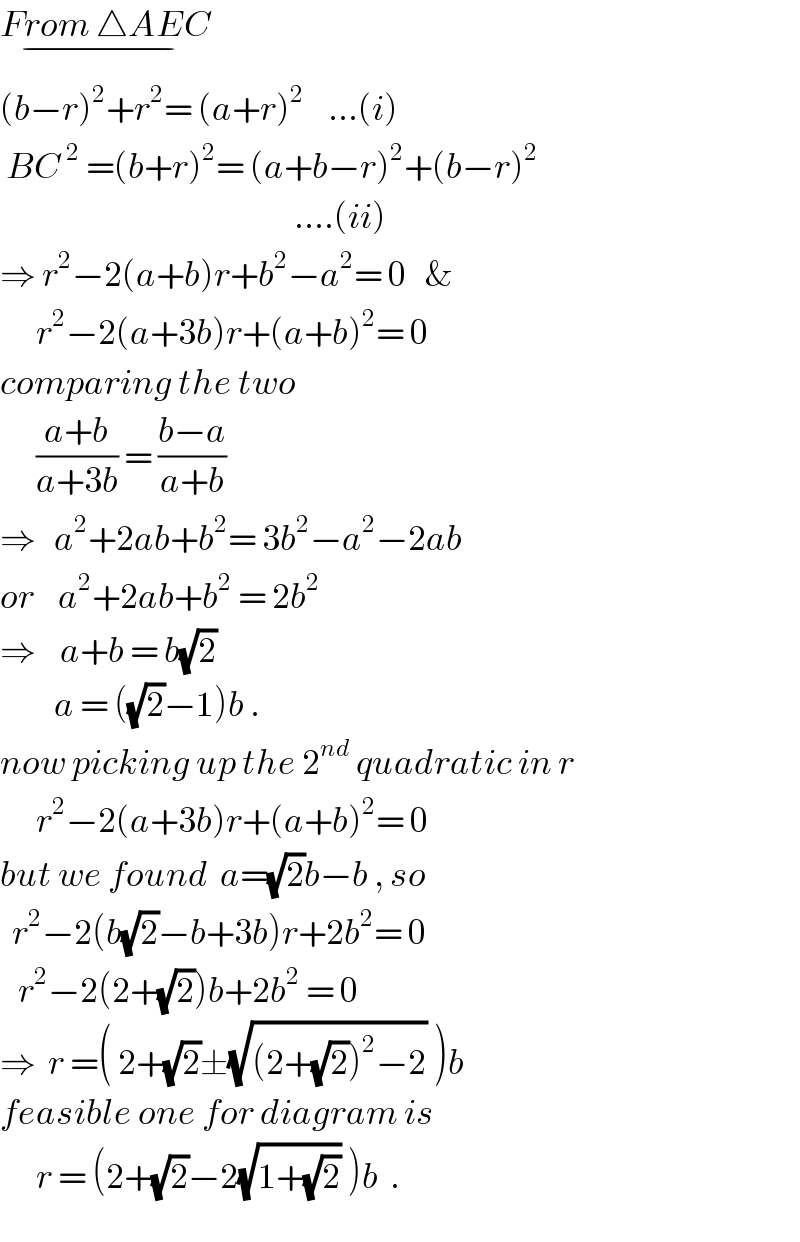
$$\underset{−} {{From}\:\bigtriangleup{AEC}} \\ $$$$\left({b}−{r}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} =\:\left({a}+{r}\right)^{\mathrm{2}} \:\:\:\:...\left({i}\right) \\ $$$$\:{BC}\:^{\mathrm{2}} \:=\left({b}+{r}\right)^{\mathrm{2}} =\:\left({a}+{b}−{r}\right)^{\mathrm{2}} +\left({b}−{r}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:....\left({ii}\right) \\ $$$$\Rightarrow\:{r}^{\mathrm{2}} −\mathrm{2}\left({a}+{b}\right){r}+{b}^{\mathrm{2}} −{a}^{\mathrm{2}} =\:\mathrm{0}\:\:\:\& \\ $$$$\:\:\:\:\:\:{r}^{\mathrm{2}} −\mathrm{2}\left({a}+\mathrm{3}{b}\right){r}+\left({a}+{b}\right)^{\mathrm{2}} =\:\mathrm{0} \\ $$$${comparing}\:{the}\:{two} \\ $$$$\:\:\:\:\:\:\frac{{a}+{b}}{{a}+\mathrm{3}{b}}\:=\:\frac{{b}−{a}}{{a}+{b}} \\ $$$$\Rightarrow\:\:\:{a}^{\mathrm{2}} +\mathrm{2}{ab}+{b}^{\mathrm{2}} =\:\mathrm{3}{b}^{\mathrm{2}} −{a}^{\mathrm{2}} −\mathrm{2}{ab} \\ $$$${or}\:\:\:\:{a}^{\mathrm{2}} +\mathrm{2}{ab}+{b}^{\mathrm{2}} \:=\:\mathrm{2}{b}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:{a}+{b}\:=\:{b}\sqrt{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:{a}\:=\:\left(\sqrt{\mathrm{2}}−\mathrm{1}\right){b}\:. \\ $$$${now}\:{picking}\:{up}\:{the}\:\mathrm{2}^{{nd}} \:{quadratic}\:{in}\:{r} \\ $$$$\:\:\:\:\:\:{r}^{\mathrm{2}} −\mathrm{2}\left({a}+\mathrm{3}{b}\right){r}+\left({a}+{b}\right)^{\mathrm{2}} =\:\mathrm{0} \\ $$$${but}\:{we}\:{found}\:\:{a}=\sqrt{\mathrm{2}}{b}−{b}\:,\:{so} \\ $$$$\:\:{r}^{\mathrm{2}} −\mathrm{2}\left({b}\sqrt{\mathrm{2}}−{b}+\mathrm{3}{b}\right){r}+\mathrm{2}{b}^{\mathrm{2}} =\:\mathrm{0} \\ $$$$\:\:\:{r}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right){b}+\mathrm{2}{b}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:{r}\:=\left(\:\mathrm{2}+\sqrt{\mathrm{2}}\pm\sqrt{\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{2}}\:\right){b} \\ $$$${feasible}\:{one}\:{for}\:{diagram}\:{is}\: \\ $$$$\:\:\:\:\:\:{r}\:=\:\left(\mathrm{2}+\sqrt{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{1}+\sqrt{\mathrm{2}}}\:\right){b}\:\:. \\ $$
Commented by mr W last updated on 20/Jan/19
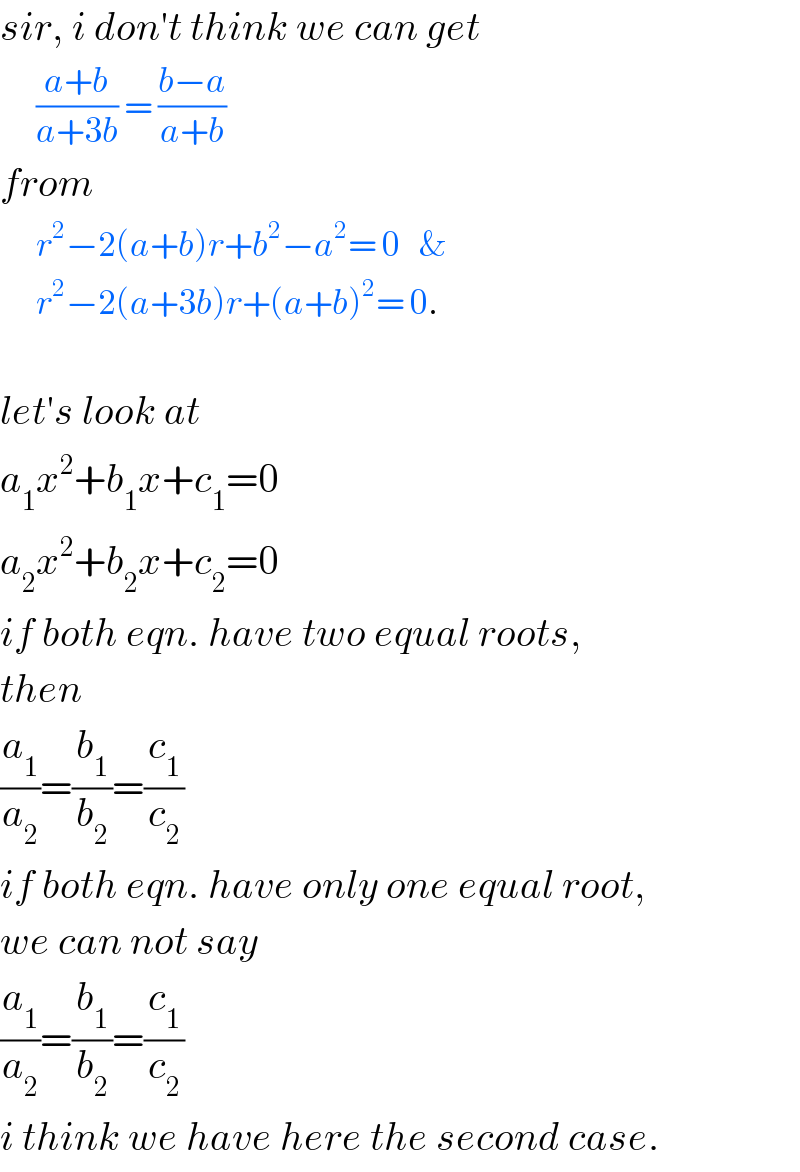
$${sir},\:{i}\:{don}'{t}\:{think}\:{we}\:{can}\:{get} \\ $$$$\:\:\:\:\:\:\frac{{a}+{b}}{{a}+\mathrm{3}{b}}\:=\:\frac{{b}−{a}}{{a}+{b}} \\ $$$${from} \\ $$$$\:\:\:\:\:\:{r}^{\mathrm{2}} −\mathrm{2}\left({a}+{b}\right){r}+{b}^{\mathrm{2}} −{a}^{\mathrm{2}} =\:\mathrm{0}\:\:\:\& \\ $$$$\:\:\:\:\:\:{r}^{\mathrm{2}} −\mathrm{2}\left({a}+\mathrm{3}{b}\right){r}+\left({a}+{b}\right)^{\mathrm{2}} =\:\mathrm{0}. \\ $$$$ \\ $$$${let}'{s}\:{look}\:{at} \\ $$$${a}_{\mathrm{1}} {x}^{\mathrm{2}} +{b}_{\mathrm{1}} {x}+{c}_{\mathrm{1}} =\mathrm{0} \\ $$$${a}_{\mathrm{2}} {x}^{\mathrm{2}} +{b}_{\mathrm{2}} {x}+{c}_{\mathrm{2}} =\mathrm{0} \\ $$$${if}\:{both}\:{eqn}.\:{have}\:{two}\:{equal}\:{roots}, \\ $$$${then} \\ $$$$\frac{{a}_{\mathrm{1}} }{{a}_{\mathrm{2}} }=\frac{{b}_{\mathrm{1}} }{{b}_{\mathrm{2}} }=\frac{{c}_{\mathrm{1}} }{{c}_{\mathrm{2}} } \\ $$$${if}\:{both}\:{eqn}.\:{have}\:{only}\:{one}\:{equal}\:{root}, \\ $$$${we}\:{can}\:{not}\:{say} \\ $$$$\frac{{a}_{\mathrm{1}} }{{a}_{\mathrm{2}} }=\frac{{b}_{\mathrm{1}} }{{b}_{\mathrm{2}} }=\frac{{c}_{\mathrm{1}} }{{c}_{\mathrm{2}} } \\ $$$${i}\:{think}\:{we}\:{have}\:{here}\:{the}\:{second}\:{case}. \\ $$
