Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 52911 by ajfour last updated on 15/Jan/19

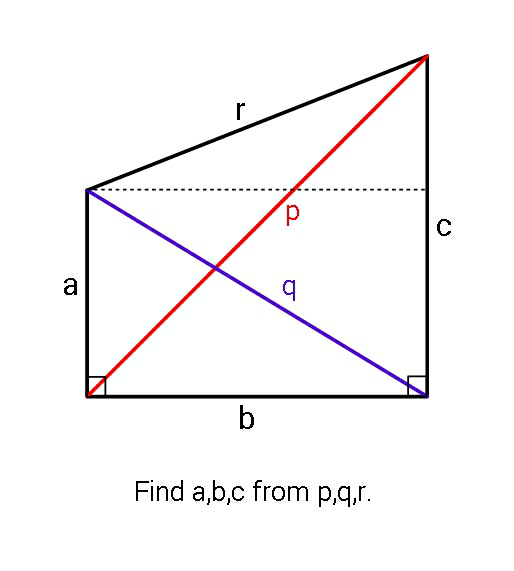
Commented by ajfour last updated on 15/Jan/19

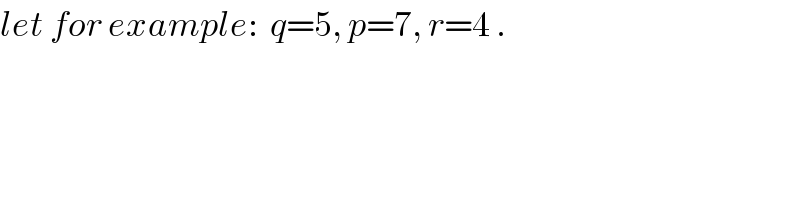
let for example: q=5, p=7, r=4 .

$${let}\:{for}\:{example}:\:\:{q}=\mathrm{5},\:{p}=\mathrm{7},\:{r}=\mathrm{4}\:. \\ $$

Commented by MJS last updated on 16/Jan/19

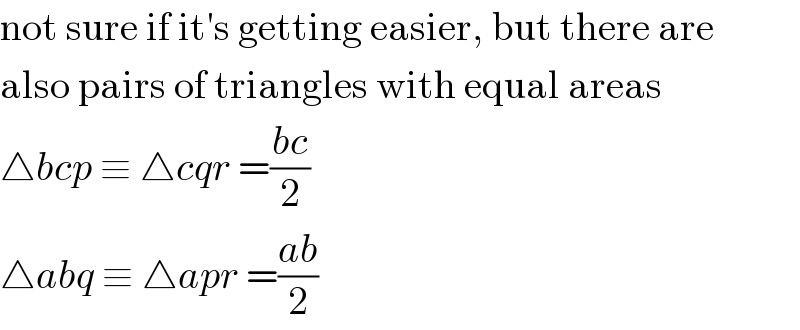
not sure if it′s getting easier, but there are also pairs of triangles with equal areas △bcp ≡ △cqr =((bc)/2) △abq ≡ △apr =((ab)/2)

$$\mathrm{not}\:\mathrm{sure}\:\mathrm{if}\:\mathrm{it}'\mathrm{s}\:\mathrm{getting}\:\mathrm{easier},\:\mathrm{but}\:\mathrm{there}\:\mathrm{are} \\ $$$$\mathrm{also}\:\mathrm{pairs}\:\mathrm{of}\:\mathrm{triangles}\:\mathrm{with}\:\mathrm{equal}\:\mathrm{areas} \\ $$$$\bigtriangleup{bcp}\:\equiv\:\bigtriangleup{cqr}\:=\frac{{bc}}{\mathrm{2}} \\ $$$$\bigtriangleup{abq}\:\equiv\:\bigtriangleup{apr}\:=\frac{{ab}}{\mathrm{2}} \\ $$

Answered by mr W last updated on 15/Jan/19

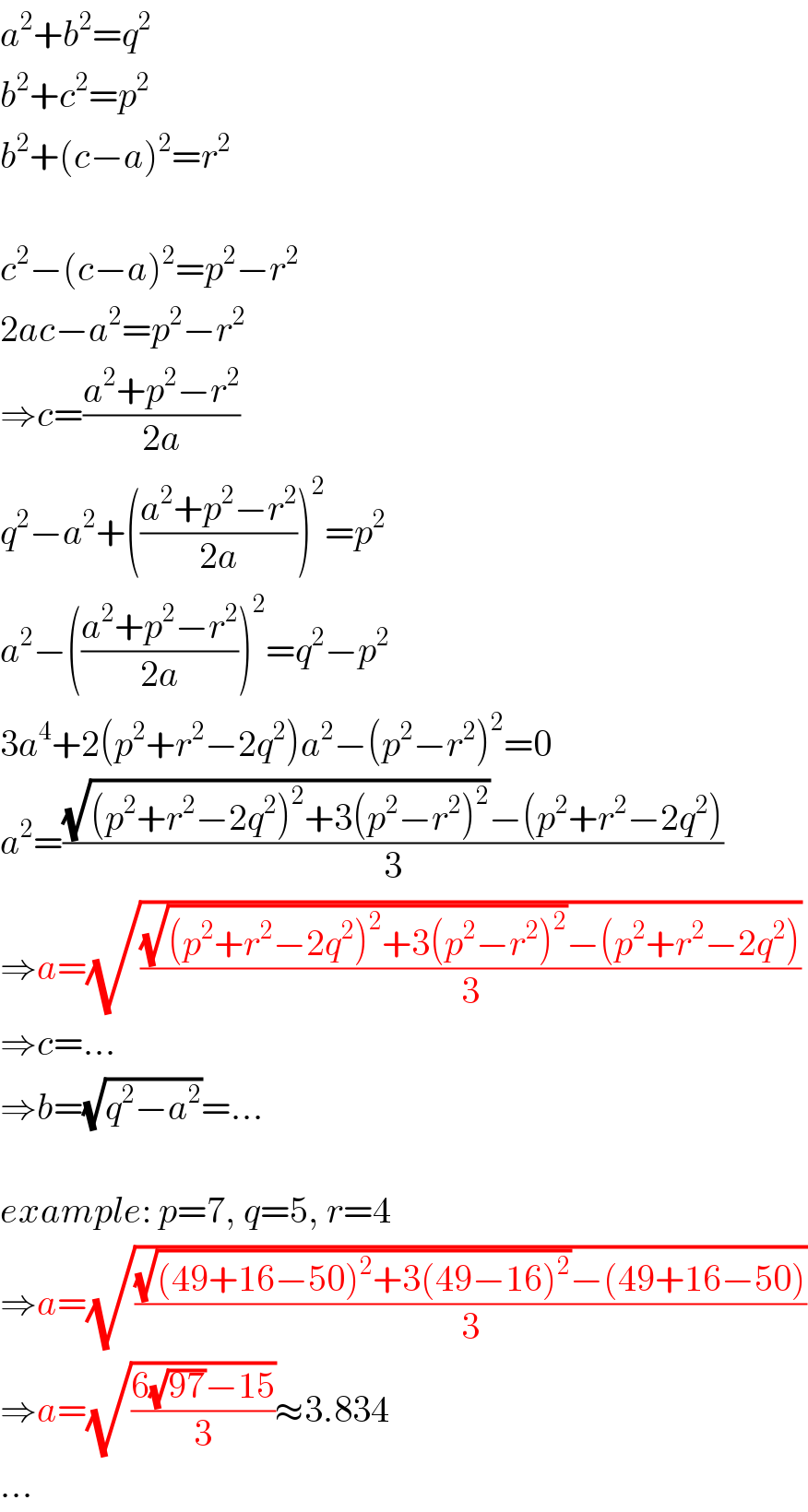
a^2 +b^2 =q^2 b^2 +c^2 =p^2 b^2 +(c−a)^2 =r^2 c^2 −(c−a)^2 =p^2 −r^2 2ac−a^2 =p^2 −r^2 ⇒c=((a^2 +p^2 −r^2 )/(2a)) q^2 −a^2 +(((a^2 +p^2 −r^2 )/(2a)))^2 =p^2 a^2 −(((a^2 +p^2 −r^2 )/(2a)))^2 =q^2 −p^2 3a^4 +2(p^2 +r^2 −2q^2 )a^2 −(p^2 −r^2 )^2 =0 a^2 =(((√((p^2 +r^2 −2q^2 )^2 +3(p^2 −r^2 )^2 ))−(p^2 +r^2 −2q^2 ))/3) ⇒a=(√(((√((p^2 +r^2 −2q^2 )^2 +3(p^2 −r^2 )^2 ))−(p^2 +r^2 −2q^2 ))/3)) ⇒c=... ⇒b=(√(q^2 −a^2 ))=... example: p=7, q=5, r=4 ⇒a=(√(((√((49+16−50)^2 +3(49−16)^2 ))−(49+16−50))/3)) ⇒a=(√((6(√(97))−15)/3))≈3.834 ...

$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={q}^{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} +{c}^{\mathrm{2}} ={p}^{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} +\left({c}−{a}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$ \\ $$$${c}^{\mathrm{2}} −\left({c}−{a}\right)^{\mathrm{2}} ={p}^{\mathrm{2}} −{r}^{\mathrm{2}} \\ $$$$\mathrm{2}{ac}−{a}^{\mathrm{2}} ={p}^{\mathrm{2}} −{r}^{\mathrm{2}} \\ $$$$\Rightarrow{c}=\frac{{a}^{\mathrm{2}} +{p}^{\mathrm{2}} −{r}^{\mathrm{2}} }{\mathrm{2}{a}} \\ $$$${q}^{\mathrm{2}} −{a}^{\mathrm{2}} +\left(\frac{{a}^{\mathrm{2}} +{p}^{\mathrm{2}} −{r}^{\mathrm{2}} }{\mathrm{2}{a}}\right)^{\mathrm{2}} ={p}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} −\left(\frac{{a}^{\mathrm{2}} +{p}^{\mathrm{2}} −{r}^{\mathrm{2}} }{\mathrm{2}{a}}\right)^{\mathrm{2}} ={q}^{\mathrm{2}} −{p}^{\mathrm{2}} \\ $$$$\mathrm{3}{a}^{\mathrm{4}} +\mathrm{2}\left({p}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{q}^{\mathrm{2}} \right){a}^{\mathrm{2}} −\left({p}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{0} \\ $$$${a}^{\mathrm{2}} =\frac{\sqrt{\left({p}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{q}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{3}\left({p}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)^{\mathrm{2}} }−\left({p}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{q}^{\mathrm{2}} \right)}{\mathrm{3}} \\ $$$$\Rightarrow{a}=\sqrt{\frac{\sqrt{\left({p}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{q}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{3}\left({p}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)^{\mathrm{2}} }−\left({p}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{q}^{\mathrm{2}} \right)}{\mathrm{3}}} \\ $$$$\Rightarrow{c}=... \\ $$$$\Rightarrow{b}=\sqrt{{q}^{\mathrm{2}} −{a}^{\mathrm{2}} }=... \\ $$$$ \\ $$$${example}:\:{p}=\mathrm{7},\:{q}=\mathrm{5},\:{r}=\mathrm{4} \\ $$$$\Rightarrow{a}=\sqrt{\frac{\sqrt{\left(\mathrm{49}+\mathrm{16}−\mathrm{50}\right)^{\mathrm{2}} +\mathrm{3}\left(\mathrm{49}−\mathrm{16}\right)^{\mathrm{2}} }−\left(\mathrm{49}+\mathrm{16}−\mathrm{50}\right)}{\mathrm{3}}} \\ $$$$\Rightarrow{a}=\sqrt{\frac{\mathrm{6}\sqrt{\mathrm{97}}−\mathrm{15}}{\mathrm{3}}}\approx\mathrm{3}.\mathrm{834} \\ $$$$... \\ $$

Commented by ajfour last updated on 15/Jan/19

Thank you Sir, this was tough for me.

$${Thank}\:{you}\:{Sir},\:{this}\:{was}\:{tough}\:{for}\:{me}. \\ $$

Answered by MJS last updated on 16/Jan/19

a=(√(((−p^2 +2q^2 −r^2 )/3)+((2(√(p^4 +q^4 +r^4 −(p^2 q^2 +p^2 r^2 +q^2 r^2 ))))/3))) b=(√(((p^2 +q^2 +r^2 )/3)−((2(√(p^4 +q^4 +r^4 −(p^2 q^2 +p^2 r^2 +q^2 r^2 ))))/3))) c=(√(((2p^2 −q^2 −r^2 )/3)+((2(√(p^4 +q^4 +r^4 −(p^2 q^2 +p^2 r^2 +q^2 r^2 ))))/3))) with p=7 q=5 r=4 I get a=(√(−5+2(√(97))))≈3.83376 b=(√(30−2(√(97))))≈3.20972 c=(√(19+2(√(97))))≈6.22075

$${a}=\sqrt{\frac{−{p}^{\mathrm{2}} +\mathrm{2}{q}^{\mathrm{2}} −{r}^{\mathrm{2}} }{\mathrm{3}}+\frac{\mathrm{2}\sqrt{{p}^{\mathrm{4}} +{q}^{\mathrm{4}} +{r}^{\mathrm{4}} −\left({p}^{\mathrm{2}} {q}^{\mathrm{2}} +{p}^{\mathrm{2}} {r}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} \right)}}{\mathrm{3}}} \\ $$$${b}=\sqrt{\frac{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} }{\mathrm{3}}−\frac{\mathrm{2}\sqrt{{p}^{\mathrm{4}} +{q}^{\mathrm{4}} +{r}^{\mathrm{4}} −\left({p}^{\mathrm{2}} {q}^{\mathrm{2}} +{p}^{\mathrm{2}} {r}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} \right)}}{\mathrm{3}}} \\ $$$${c}=\sqrt{\frac{\mathrm{2}{p}^{\mathrm{2}} −{q}^{\mathrm{2}} −{r}^{\mathrm{2}} }{\mathrm{3}}+\frac{\mathrm{2}\sqrt{{p}^{\mathrm{4}} +{q}^{\mathrm{4}} +{r}^{\mathrm{4}} −\left({p}^{\mathrm{2}} {q}^{\mathrm{2}} +{p}^{\mathrm{2}} {r}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} \right)}}{\mathrm{3}}} \\ $$$$\mathrm{with}\:{p}=\mathrm{7}\:{q}=\mathrm{5}\:{r}=\mathrm{4}\:\mathrm{I}\:\mathrm{get} \\ $$$${a}=\sqrt{−\mathrm{5}+\mathrm{2}\sqrt{\mathrm{97}}}\approx\mathrm{3}.\mathrm{83376} \\ $$$${b}=\sqrt{\mathrm{30}−\mathrm{2}\sqrt{\mathrm{97}}}\approx\mathrm{3}.\mathrm{20972} \\ $$$${c}=\sqrt{\mathrm{19}+\mathrm{2}\sqrt{\mathrm{97}}}\approx\mathrm{6}.\mathrm{22075} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com