Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 5190 by sanusihammed last updated on 28/Apr/16

Commented by prakash jain last updated on 29/Apr/16

((AB)/(BO))=((CD)/(DO)) (5/6)=(x/4) x=((20)/6)

$$\frac{\mathrm{AB}}{\mathrm{BO}}=\frac{\mathrm{CD}}{\mathrm{DO}} \\ $$$$\frac{\mathrm{5}}{\mathrm{6}}=\frac{{x}}{\mathrm{4}} \\ $$$${x}=\frac{\mathrm{20}}{\mathrm{6}} \\ $$

Commented by Rasheed Soomro last updated on 01/May/16

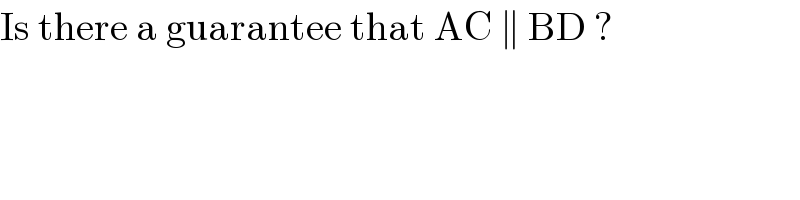
Is there a guarantee that AC ∥ BD ?

$$\mathrm{Is}\:\mathrm{there}\:\mathrm{a}\:\mathrm{guarantee}\:\mathrm{that}\:\mathrm{AC}\:\parallel\:\mathrm{BD}\:? \\ $$

Commented by Rasheed Soomro last updated on 02/May/16

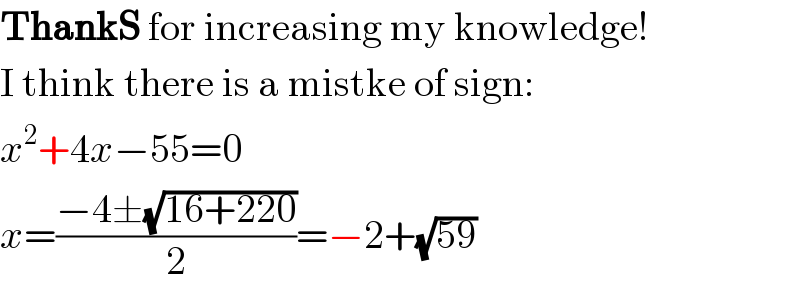
ThankS for increasing my knowledge! I think there is a mistke of sign: x^2 +4x−55=0 x=((−4±(√(16+220)))/2)=−2+(√(59))

$$\boldsymbol{\mathrm{ThankS}}\:\mathrm{for}\:\mathrm{increasing}\:\mathrm{my}\:\mathrm{knowledge}! \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{there}\:\mathrm{is}\:\mathrm{a}\:\mathrm{mistke}\:\mathrm{of}\:\mathrm{sign}: \\ $$$${x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{55}=\mathrm{0} \\ $$$${x}=\frac{−\mathrm{4}\pm\sqrt{\mathrm{16}+\mathrm{220}}}{\mathrm{2}}=−\mathrm{2}+\sqrt{\mathrm{59}} \\ $$

Commented by prakash jain last updated on 01/May/16

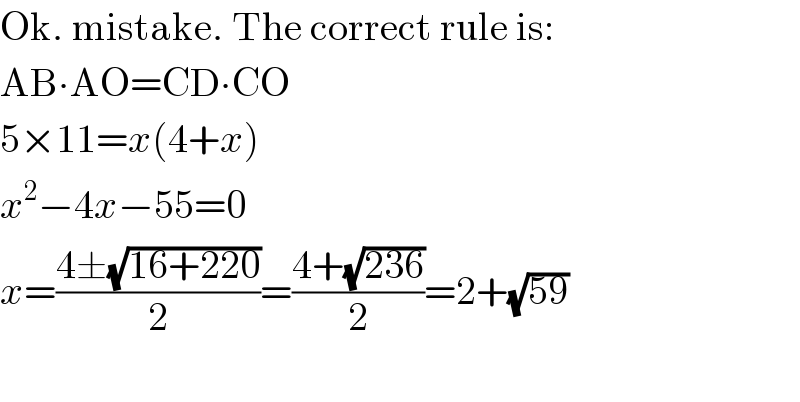
Ok. mistake. The correct rule is: AB∙AO=CD∙CO 5×11=x(4+x) x^2 −4x−55=0 x=((4±(√(16+220)))/2)=((4+(√(236)))/2)=2+(√(59))

$$\mathrm{Ok}.\:\mathrm{mistake}.\:\mathrm{The}\:\mathrm{correct}\:\mathrm{rule}\:\mathrm{is}: \\ $$$$\mathrm{AB}\centerdot\mathrm{AO}=\mathrm{CD}\centerdot\mathrm{CO} \\ $$$$\mathrm{5}×\mathrm{11}={x}\left(\mathrm{4}+{x}\right) \\ $$$${x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{55}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{4}\pm\sqrt{\mathrm{16}+\mathrm{220}}}{\mathrm{2}}=\frac{\mathrm{4}+\sqrt{\mathrm{236}}}{\mathrm{2}}=\mathrm{2}+\sqrt{\mathrm{59}} \\ $$$$ \\ $$

Commented by prakash jain last updated on 02/May/16

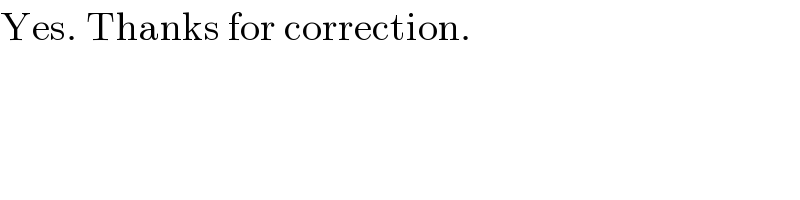
Yes. Thanks for correction.

$$\mathrm{Yes}.\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{correction}. \\ $$

Answered by prakash jain last updated on 29/Apr/16

In triangle ABC AB=AC=11 BC=9 Draw altitude BX. Since AB=AC BX=XC=4.5 AX=(√(11^2 +4.5^2 )) If O is center AX will pass thru O. Draw ⊥^r from O to AB. Let it intersect AB at D. D is mid point of AB. AOD is right angle triangle. AO=(√(5.5^2 +DO^2 )) In triangle BOX (also a right angle triangle) BO=(√(4.5^2 +OX^2 )) AO=BO=r AO+OX=AX=(√(11^2 +4.5^2 )) r+OX=(√(11^2 +4.5^2 )) ...(A) r=(√(4.5^2 +OX^2 )) ...(B) solve for r using A and B

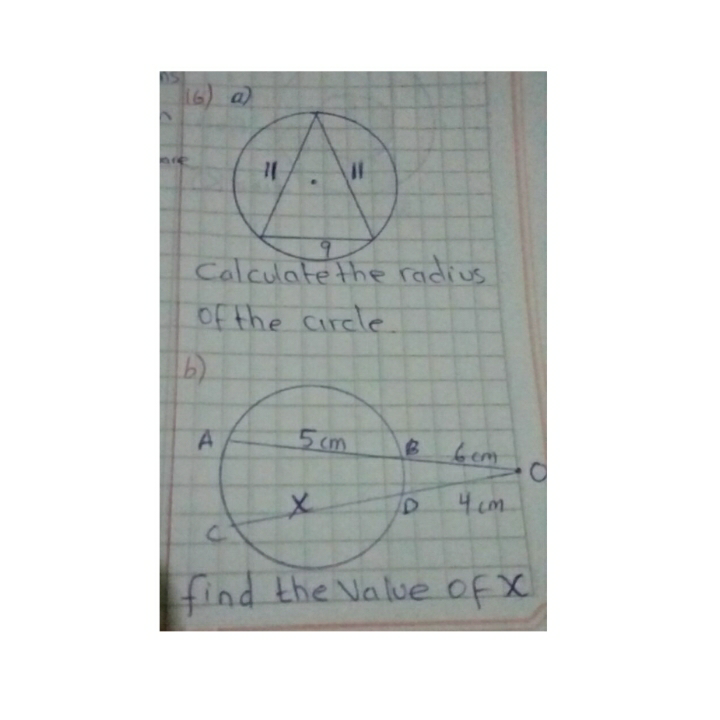
$$\mathrm{In}\:\mathrm{triangle}\:\mathrm{ABC} \\ $$$$\mathrm{AB}=\mathrm{AC}=\mathrm{11} \\ $$$$\mathrm{BC}=\mathrm{9} \\ $$$$\mathrm{Draw}\:\mathrm{altitude}\:\mathrm{BX}.\: \\ $$$$\mathrm{Since}\:\mathrm{AB}=\mathrm{AC} \\ $$$$\mathrm{BX}=\mathrm{XC}=\mathrm{4}.\mathrm{5} \\ $$$$\mathrm{AX}=\sqrt{\mathrm{11}^{\mathrm{2}} +\mathrm{4}.\mathrm{5}^{\mathrm{2}} } \\ $$$$\mathrm{If}\:\mathrm{O}\:\mathrm{is}\:\mathrm{center}\:\mathrm{AX}\:\mathrm{will}\:\mathrm{pass}\:\mathrm{thru}\:\mathrm{O}. \\ $$$$\mathrm{Draw}\:\bot^{{r}} \:\mathrm{from}\:\mathrm{O}\:\mathrm{to}\:\mathrm{AB}.\:\mathrm{Let}\:\mathrm{it}\:\mathrm{intersect}\:\mathrm{AB} \\ $$$$\mathrm{at}\:\mathrm{D}.\:\mathrm{D}\:\mathrm{is}\:\mathrm{mid}\:\mathrm{point}\:\mathrm{of}\:\mathrm{AB}. \\ $$$$\mathrm{AOD}\:\mathrm{is}\:\mathrm{right}\:\mathrm{angle}\:\mathrm{triangle}. \\ $$$$\mathrm{AO}=\sqrt{\mathrm{5}.\mathrm{5}^{\mathrm{2}} +\mathrm{DO}^{\mathrm{2}} } \\ $$$$\mathrm{In}\:\mathrm{triangle}\:\mathrm{BOX}\:\left(\mathrm{also}\:\mathrm{a}\:\mathrm{right}\:\mathrm{angle}\:\mathrm{triangle}\right) \\ $$$$\mathrm{BO}=\sqrt{\mathrm{4}.\mathrm{5}^{\mathrm{2}} +\mathrm{OX}^{\mathrm{2}} } \\ $$$$\mathrm{AO}=\mathrm{BO}={r} \\ $$$$\mathrm{AO}+\mathrm{OX}=\mathrm{AX}=\sqrt{\mathrm{11}^{\mathrm{2}} +\mathrm{4}.\mathrm{5}^{\mathrm{2}} } \\ $$$${r}+\mathrm{OX}=\sqrt{\mathrm{11}^{\mathrm{2}} +\mathrm{4}.\mathrm{5}^{\mathrm{2}} }\:\:\:...\left(\mathrm{A}\right) \\ $$$${r}=\sqrt{\mathrm{4}.\mathrm{5}^{\mathrm{2}} +\mathrm{OX}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:...\left(\mathrm{B}\right) \\ $$$$\mathrm{solve}\:\mathrm{for}\:{r}\:\mathrm{using}\:\mathrm{A}\:\mathrm{and}\:\mathrm{B} \\ $$

Answered by Rasheed Soomro last updated on 01/May/16

(a) If a, b, c are measures of sides of a triangle and ▲ is its area, then circum-radius R will be R=((abc)/(4▲)) Here a=b=11 and c=9 s=((a+b+c)/2)=((11+11+9)/2)=15.5 ▲=(√(s(s−a)(s−b)(s−c))) =(√(15.5(15.5−11)^2 (15.5−9)))=45.168 So, R=((11×11×9)/(4×45.168))=6.027

$$\left({a}\right) \\ $$$$\mathrm{If}\:\mathrm{a},\:\mathrm{b},\:\mathrm{c}\:\mathrm{are}\:\mathrm{measures}\:\mathrm{of}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{a} \\ $$$$\mathrm{triangle}\:\mathrm{and}\:\blacktriangle\:\mathrm{is}\:\mathrm{its}\:\mathrm{area},\:\mathrm{then} \\ $$$$\mathrm{circum}-\mathrm{radius}\:\mathrm{R}\:\mathrm{will}\:\mathrm{be} \\ $$$$\mathrm{R}=\frac{\mathrm{abc}}{\mathrm{4}\blacktriangle} \\ $$$$\mathrm{Here}\:\mathrm{a}=\mathrm{b}=\mathrm{11}\:\mathrm{and}\:\mathrm{c}=\mathrm{9} \\ $$$$\mathrm{s}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{2}}=\frac{\mathrm{11}+\mathrm{11}+\mathrm{9}}{\mathrm{2}}=\mathrm{15}.\mathrm{5} \\ $$$$\blacktriangle=\sqrt{\mathrm{s}\left(\mathrm{s}−\mathrm{a}\right)\left(\mathrm{s}−\mathrm{b}\right)\left(\mathrm{s}−\mathrm{c}\right)} \\ $$$$\:\:\:=\sqrt{\mathrm{15}.\mathrm{5}\left(\mathrm{15}.\mathrm{5}−\mathrm{11}\right)^{\mathrm{2}} \left(\mathrm{15}.\mathrm{5}−\mathrm{9}\right)}=\mathrm{45}.\mathrm{168} \\ $$$$\mathrm{So}, \\ $$$$\:\:\:\:\:\:\mathrm{R}=\frac{\mathrm{11}×\mathrm{11}×\mathrm{9}}{\mathrm{4}×\mathrm{45}.\mathrm{168}}=\mathrm{6}.\mathrm{027} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com