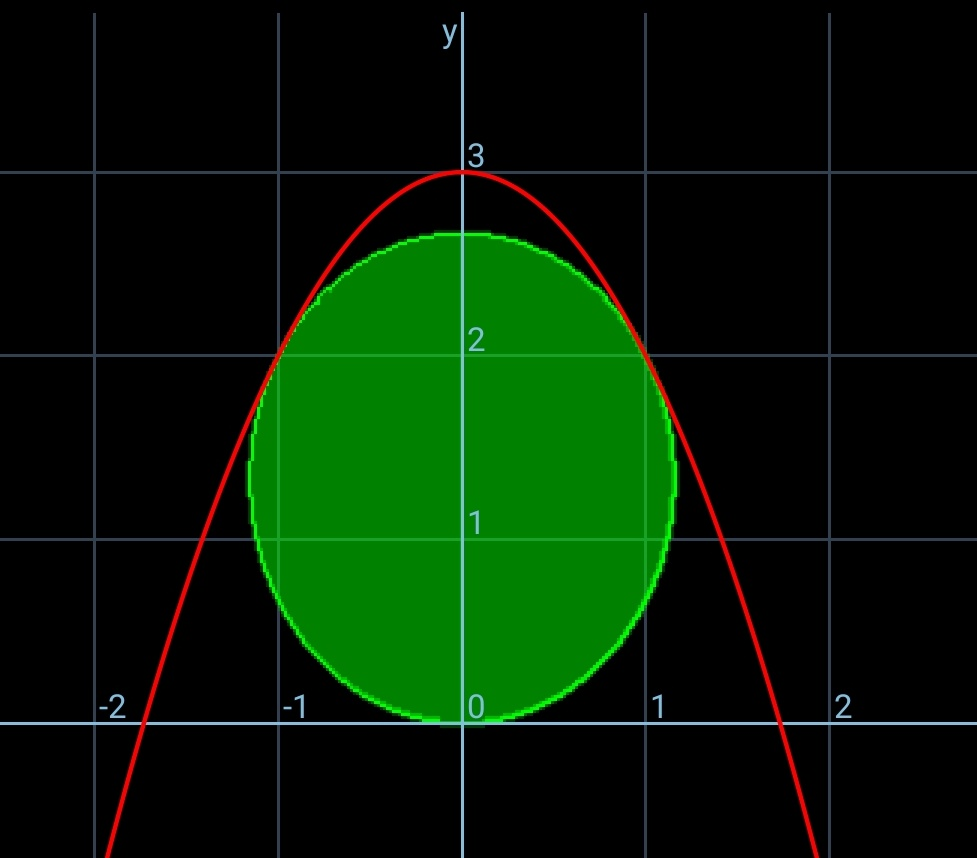
Question Number 49394 by ajfour last updated on 06/Dec/18
Commented by ajfour last updated on 07/Dec/18
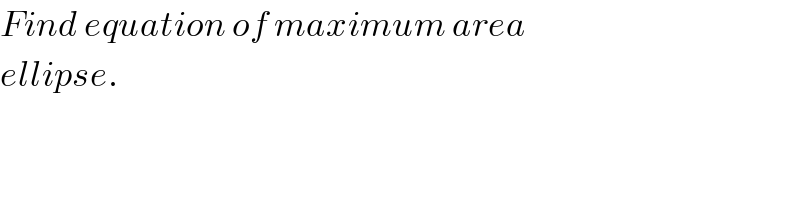
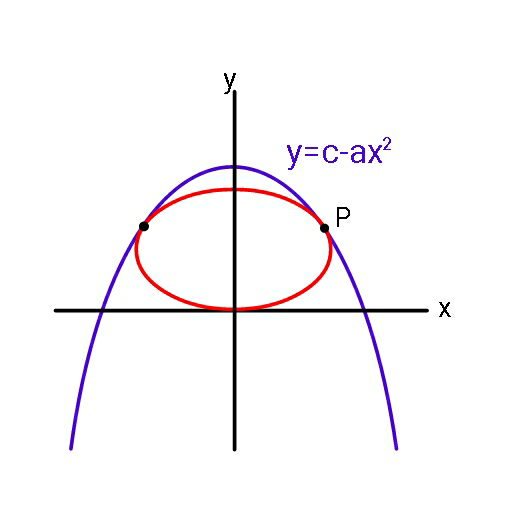
$${Find}\:{equation}\:{of}\:{maximum}\:{area} \\ $$$${ellipse}. \\ $$
Answered by ajfour last updated on 06/Dec/18
![y=c−ax^2 (x^2 /p^2 )+(((y−q)^2 )/q^2 ) = 1 (x^2 /p^2 )+(((c−ax^2 −q)^2 )/q^2 ) = 1 p^2 a^2 x^4 +[q^2 −2a(c−q)p^2 ]x^2 +p^2 [(c−q)^2 −q^2 ] = 0 so for tangency [q^2 −2a(c−q)p^2 ]^2 =4a^2 p^4 [(c−q)^2 −q^2 ) ⇒ q^4 −4a(c−q)p^2 q^2 +4a^2 p^4 q^2 = 0 or q^2 −4a(c−q)p^2 +4a^2 p^4 = 0 ...(i) let A=p^2 q^2 ⇒ q^4 −4a(c−q)A+((4a^2 A^2 )/q^2 ) = 0 ⇒ 4a^2 A^2 −4aq^2 (c−q)A+q^6 = 0 ⇒ (8a^2 A)(dA/dq)−4aq^2 (c−q)(dA/dq) +(12aq^2 −8acq)A+6q^5 = 0 (dA/dq) = 0 ⇒ A(12aq^2 −8acq)= −6q^5 ⇒ 2ap^2 (2c−3q)= 3q^2 ....(ii) using p^2 =((3q^2 )/(2a(2c−3q))) in ..(i) q^2 −4a(c−q)[((3q^2 )/(2a(2c−3q)))]+4a^2 [((3q^2 )/(2a(2c−3q)))]^2 = 0 ⇒ 4a^2 q^2 (2c−3q)^2 −24a^2 q^2 (c−q)(2c−3q) 36a^2 q^4 = 0 ⇒ (2c−3q)^2 −6(c−q)(2c−3q) +9q^2 = 0 ⇒ 9q^2 +4c^2 −12cq−12c^2 +30cq −18q^2 +9q^2 = 0 _________________________ ⇒ q = ((4c)/9) and from (i), p^2 =((3q^2 )/(2a(2c−3q))) = (((((16c^2 )/(27))))/(2a(((2c)/3)))) = ((4c)/(9a)) eq. of ellipse is then ((9ax^2 )/(4c))+((81(y−((4c)/9))^2 )/(16c^2 )) = 1 _________________________ .](Q49399.png)
$${y}={c}−{ax}^{\mathrm{2}} \\ $$$$\frac{{x}^{\mathrm{2}} }{{p}^{\mathrm{2}} }+\frac{\left({y}−{q}\right)^{\mathrm{2}} }{{q}^{\mathrm{2}} }\:=\:\mathrm{1} \\ $$$$\:\:\frac{{x}^{\mathrm{2}} }{{p}^{\mathrm{2}} }+\frac{\left({c}−{ax}^{\mathrm{2}} −{q}\right)^{\mathrm{2}} }{{q}^{\mathrm{2}} }\:=\:\mathrm{1} \\ $$$$\:\:{p}^{\mathrm{2}} {a}^{\mathrm{2}} {x}^{\mathrm{4}} +\left[{q}^{\mathrm{2}} −\mathrm{2}{a}\left({c}−{q}\right){p}^{\mathrm{2}} \right]{x}^{\mathrm{2}} +{p}^{\mathrm{2}} \left[\left({c}−{q}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right]\:=\:\mathrm{0} \\ $$$${so}\:{for}\:{tangency} \\ $$$$\left[{q}^{\mathrm{2}} −\mathrm{2}{a}\left({c}−{q}\right){p}^{\mathrm{2}} \right]^{\mathrm{2}} =\mathrm{4}{a}^{\mathrm{2}} {p}^{\mathrm{4}} \left[\left({c}−{q}\right)^{\mathrm{2}} −{q}^{\mathrm{2}} \right)\:\:\:\: \\ $$$$\Rightarrow\:\:{q}^{\mathrm{4}} −\mathrm{4}{a}\left({c}−{q}\right){p}^{\mathrm{2}} {q}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} {p}^{\mathrm{4}} {q}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$${or}\:\:\:{q}^{\mathrm{2}} −\mathrm{4}{a}\left({c}−{q}\right){p}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} {p}^{\mathrm{4}} \:=\:\mathrm{0}\:\:...\left({i}\right) \\ $$$${let}\:{A}={p}^{\mathrm{2}} {q}^{\mathrm{2}} \:\:\:\Rightarrow \\ $$$$\:\:{q}^{\mathrm{4}} −\mathrm{4}{a}\left({c}−{q}\right){A}+\frac{\mathrm{4}{a}^{\mathrm{2}} {A}^{\mathrm{2}} }{{q}^{\mathrm{2}} }\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{4}{a}^{\mathrm{2}} {A}^{\mathrm{2}} −\mathrm{4}{aq}^{\mathrm{2}} \left({c}−{q}\right){A}+{q}^{\mathrm{6}} \:=\:\mathrm{0} \\ $$$$\Rightarrow\:\left(\mathrm{8}{a}^{\mathrm{2}} {A}\right)\frac{{dA}}{{dq}}−\mathrm{4}{aq}^{\mathrm{2}} \left({c}−{q}\right)\frac{{dA}}{{dq}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(\mathrm{12}{aq}^{\mathrm{2}} −\mathrm{8}{acq}\right){A}+\mathrm{6}{q}^{\mathrm{5}} \:=\:\mathrm{0} \\ $$$$\frac{{dA}}{{dq}}\:=\:\mathrm{0}\:\:\:\Rightarrow \\ $$$$\:\:\:{A}\left(\mathrm{12}{aq}^{\mathrm{2}} −\mathrm{8}{acq}\right)=\:−\mathrm{6}{q}^{\mathrm{5}} \\ $$$$\Rightarrow\:\mathrm{2}{ap}^{\mathrm{2}} \left(\mathrm{2}{c}−\mathrm{3}{q}\right)=\:\mathrm{3}{q}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:....\left({ii}\right) \\ $$$${using}\:\:\:{p}^{\mathrm{2}} =\frac{\mathrm{3}{q}^{\mathrm{2}} }{\mathrm{2}{a}\left(\mathrm{2}{c}−\mathrm{3}{q}\right)}\:\:\:\:{in}\:\:..\left({i}\right) \\ $$$$\:\:{q}^{\mathrm{2}} −\mathrm{4}{a}\left({c}−{q}\right)\left[\frac{\mathrm{3}{q}^{\mathrm{2}} }{\mathrm{2}{a}\left(\mathrm{2}{c}−\mathrm{3}{q}\right)}\right]+\mathrm{4}{a}^{\mathrm{2}} \left[\frac{\mathrm{3}{q}^{\mathrm{2}} }{\mathrm{2}{a}\left(\mathrm{2}{c}−\mathrm{3}{q}\right)}\right]^{\mathrm{2}} =\:\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\mathrm{4}{a}^{\mathrm{2}} {q}^{\mathrm{2}} \left(\mathrm{2}{c}−\mathrm{3}{q}\right)^{\mathrm{2}} −\mathrm{24}{a}^{\mathrm{2}} {q}^{\mathrm{2}} \left({c}−{q}\right)\left(\mathrm{2}{c}−\mathrm{3}{q}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{36}{a}^{\mathrm{2}} {q}^{\mathrm{4}} \:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\left(\mathrm{2}{c}−\mathrm{3}{q}\right)^{\mathrm{2}} −\mathrm{6}\left({c}−{q}\right)\left(\mathrm{2}{c}−\mathrm{3}{q}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{9}{q}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{9}\boldsymbol{{q}}^{\mathrm{2}} +\mathrm{4}\boldsymbol{{c}}^{\mathrm{2}} −\mathrm{12}\boldsymbol{{cq}}−\mathrm{12}\boldsymbol{{c}}^{\mathrm{2}} +\mathrm{30}\boldsymbol{{cq}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{18}\boldsymbol{{q}}^{\mathrm{2}} +\mathrm{9}\boldsymbol{{q}}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\Rightarrow\:\:{q}\:=\:\frac{\mathrm{4}{c}}{\mathrm{9}}\:\:\:{and}\:{from}\:\left({i}\right), \\ $$$${p}^{\mathrm{2}} =\frac{\mathrm{3}{q}^{\mathrm{2}} }{\mathrm{2}{a}\left(\mathrm{2}{c}−\mathrm{3}{q}\right)}\:\:=\:\frac{\left(\frac{\mathrm{16}{c}^{\mathrm{2}} }{\mathrm{27}}\right)}{\mathrm{2}{a}\left(\frac{\mathrm{2}{c}}{\mathrm{3}}\right)}\:=\:\frac{\mathrm{4}{c}}{\mathrm{9}{a}} \\ $$$$\:\:\:{eq}.\:{of}\:{ellipse}\:{is}\:{then} \\ $$$$\:\:\:\:\:\frac{\mathrm{9}\boldsymbol{{ax}}^{\mathrm{2}} }{\mathrm{4}\boldsymbol{{c}}}+\frac{\mathrm{81}\left(\boldsymbol{{y}}−\frac{\mathrm{4}\boldsymbol{{c}}}{\mathrm{9}}\right)^{\mathrm{2}} }{\mathrm{16}\boldsymbol{{c}}^{\mathrm{2}} }\:=\:\mathrm{1}\: \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\:. \\ $$
Commented by mr W last updated on 06/Dec/18

$${very}\:{fine}\:{sir}! \\ $$
Commented by ajfour last updated on 06/Dec/18

$${yes}\:{sir},\:{would}\:{you}\:{check}\:{the} \\ $$$${solution}\:{again},\:{please}.. \\ $$
Commented by mr W last updated on 06/Dec/18