
Question Number 49280 by mr W last updated on 05/Dec/18
Commented by mr W last updated on 05/Dec/18

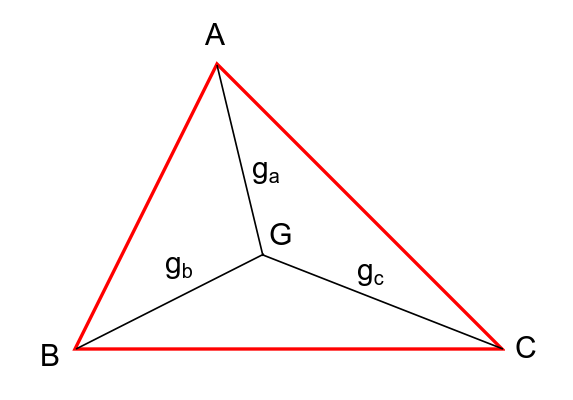
$${The}\:{distances}\:{from}\:{its}\:{centroid}\:{to} \\ $$$${its}\:{vertices}\:{are}\:{given}.\:{Find}\:{the}\:{area} \\ $$$${of}\:{the}\:{triangle}. \\ $$
Commented by behi83417@gmail.com last updated on 05/Dec/18

$${g}_{{a}} =\frac{\mathrm{2}}{\mathrm{3}}{m}_{{a}} =\frac{\mathrm{1}}{\mathrm{3}}\sqrt{\mathrm{2}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−{a}^{\mathrm{2}} }= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−\mathrm{3}{a}^{\mathrm{2}} }= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\sqrt{\mathrm{2}×\frac{\mathrm{4}}{\mathrm{3}}\Sigma{m}_{{a}} ^{\mathrm{2}} −\mathrm{3}{a}^{\mathrm{2}} }= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\sqrt{\frac{\mathrm{8}}{\mathrm{3}}.\frac{\mathrm{9}}{\mathrm{4}}\Sigma{g}_{{a}} ^{\mathrm{2}} −\mathrm{3}{a}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{3}}\sqrt{\mathrm{6}\Sigma{g}_{{a}} ^{\mathrm{2}} −\mathrm{3}{a}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{3}{g}_{{a}} ^{\mathrm{2}} =\mathrm{2}\left({g}_{{a}} ^{\mathrm{2}} +{g}_{{b}} ^{\mathrm{2}} +{g}_{{c}} ^{\mathrm{2}} \right)−{a}^{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} =\mathrm{2}\left({g}_{{b}} ^{\mathrm{2}} +{g}_{{c}} ^{\mathrm{2}} \right)−{g}_{{a}} ^{\mathrm{2}} \Rightarrow \\ $$$$\boldsymbol{\mathrm{a}}=\sqrt{\mathrm{2}\left(\boldsymbol{\mathrm{g}}_{\boldsymbol{\mathrm{b}}} ^{\mathrm{2}} +\boldsymbol{\mathrm{g}}_{\boldsymbol{\mathrm{c}}} ^{\mathrm{2}} \right)−\boldsymbol{\mathrm{g}}_{\boldsymbol{\mathrm{a}}} ^{\mathrm{2}} } \\ $$$$\boldsymbol{\mathrm{b}}=\sqrt{\mathrm{2}\left(\boldsymbol{\mathrm{g}}_{\boldsymbol{\mathrm{a}}} ^{\mathrm{2}} +\boldsymbol{\mathrm{g}}_{\boldsymbol{\mathrm{c}}} ^{\mathrm{2}} \right)−\boldsymbol{\mathrm{g}}_{\boldsymbol{\mathrm{b}}} ^{\mathrm{2}} } \\ $$$$\boldsymbol{\mathrm{c}}=\sqrt{\mathrm{2}\left(\boldsymbol{\mathrm{g}}_{\boldsymbol{\mathrm{a}}} ^{\mathrm{2}} +\boldsymbol{\mathrm{g}}_{\boldsymbol{\mathrm{b}}} ^{\mathrm{2}} \right)−\boldsymbol{\mathrm{g}}_{\boldsymbol{\mathrm{c}}} ^{\mathrm{2}} } \\ $$$$\boldsymbol{\mathrm{now}}\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{area}}\:\boldsymbol{\mathrm{from}}:{Heron}'{s}\:\boldsymbol{\mathrm{formula}}. \\ $$$$\boldsymbol{\mathrm{note}}:\Sigma{m}_{{a}} ^{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{4}}\Sigma{a}^{\mathrm{2}} . \\ $$
Commented by mr W last updated on 05/Dec/18

$${thanks}\:{sir}! \\ $$
Answered by MJS last updated on 05/Dec/18

$${A}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\:{B}=\begin{pmatrix}{{c}}\\{\mathrm{0}}\end{pmatrix}\:\:{C}=\begin{pmatrix}{\frac{−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{c}}}\\{\frac{\delta\left({a},\:{b},\:{c}\right)}{\mathrm{2}{c}}}\end{pmatrix} \\ $$$$\delta\left({a},\:{b},\:{c}\right)=\sqrt{\left({a}+{b}+{c}\right)\left({a}+{b}−{c}\right)\left({a}−{b}+{c}\right)\left(−{a}+{b}+{c}\right)} \\ $$$${G}=\begin{pmatrix}{\frac{−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{3}{c}^{\mathrm{2}} }{\mathrm{6}{c}}}\\{\frac{\delta\left({a},\:{b},\:{c}\right)}{\mathrm{6}{c}}}\end{pmatrix} \\ $$$${g}_{{a}} ^{\mathrm{2}} =\frac{−{a}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} +\mathrm{2}{c}^{\mathrm{2}} }{\mathrm{9}} \\ $$$${g}_{{b}} ^{\mathrm{2}} =\frac{\mathrm{2}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +\mathrm{2}{c}^{\mathrm{2}} }{\mathrm{9}} \\ $$$${g}_{{c}} ^{\mathrm{2}} =\frac{\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{9}} \\ $$$$\Rightarrow \\ $$$${a}^{\mathrm{2}} =−{g}_{{a}} ^{\mathrm{2}} +\mathrm{2}{g}_{{b}} ^{\mathrm{2}} +\mathrm{2}{g}_{{c}} ^{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} =\mathrm{2}{g}_{{a}} ^{\mathrm{2}} −{g}_{{b}} ^{\mathrm{2}} +\mathrm{2}{g}_{{c}} ^{\mathrm{2}} \\ $$$${c}^{\mathrm{2}} =\mathrm{2}{g}_{{a}} ^{\mathrm{2}} +\mathrm{2}{g}_{{b}} ^{\mathrm{2}} −{g}_{{c}} ^{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\mathrm{area}\left({a},\:{b},\:{c}\right)=\frac{\delta\left({a},\:{b},\:{c}\right)}{\mathrm{4}}=\frac{\mathrm{3}\delta\left({g}_{{a}} ,\:{g}_{{b}} ,\:{g}_{{c}} \right)}{\mathrm{4}} \\ $$
Commented by mr W last updated on 05/Dec/18
$${thank}\:{you}\:{sir}! \\ $$$${the}\:{last}\:{line}\:{is}\:{new}\:{to}\:{me},\:{very}\:{nice}! \\ $$
Commented by MJS last updated on 05/Dec/18

$$\mathrm{it}'\mathrm{s}\:\mathrm{just}\:\mathrm{Heron}'\mathrm{s}\:\mathrm{sentence} \\ $$
Commented by mr W last updated on 05/Dec/18
Commented by mr W last updated on 05/Dec/18

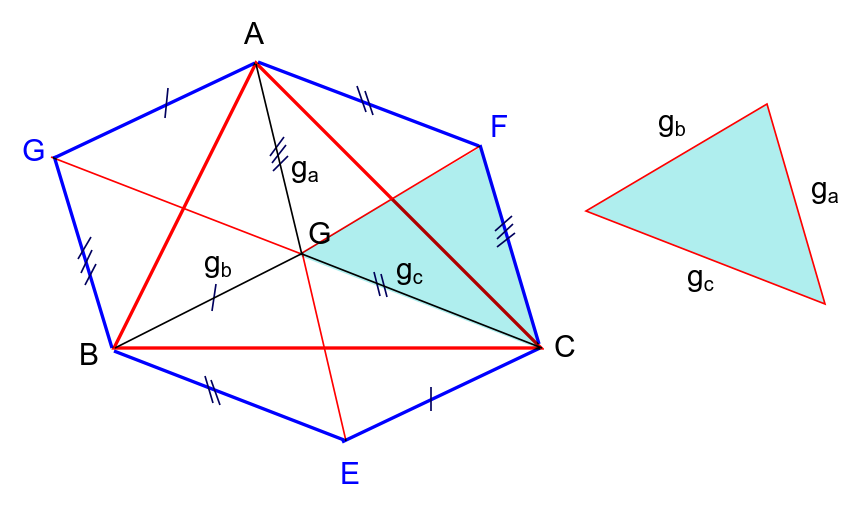
$${Area}\:{of}\:{hexagon}=\mathrm{2}×{Area}\:{of}\:\Delta{ABC} \\ $$$${Area}\:{of}\:{hexagon}=\mathrm{6}×{Area}\:{of}\:{triangle}\:{with}\:{sides}\:{g}_{{a}} ,{g}_{{b}} ,{g}_{{c}} \\ $$$$\Rightarrow{Area}\:{of}\:\Delta{ABC}=\mathrm{3}×{Area}\:{of}\:{triangle}\:{with}\:{sides}\:{g}_{{a}} ,{g}_{{b}} ,{g}_{{c}} \\ $$
Commented by mr W last updated on 05/Dec/18
$${Now}\:{I}\:{understand}\:{it}\:{geometrically}. \\ $$
