
Question Number 49256 by munnabhai455111@gmail.com last updated on 05/Dec/18

Answered by afachri last updated on 05/Dec/18
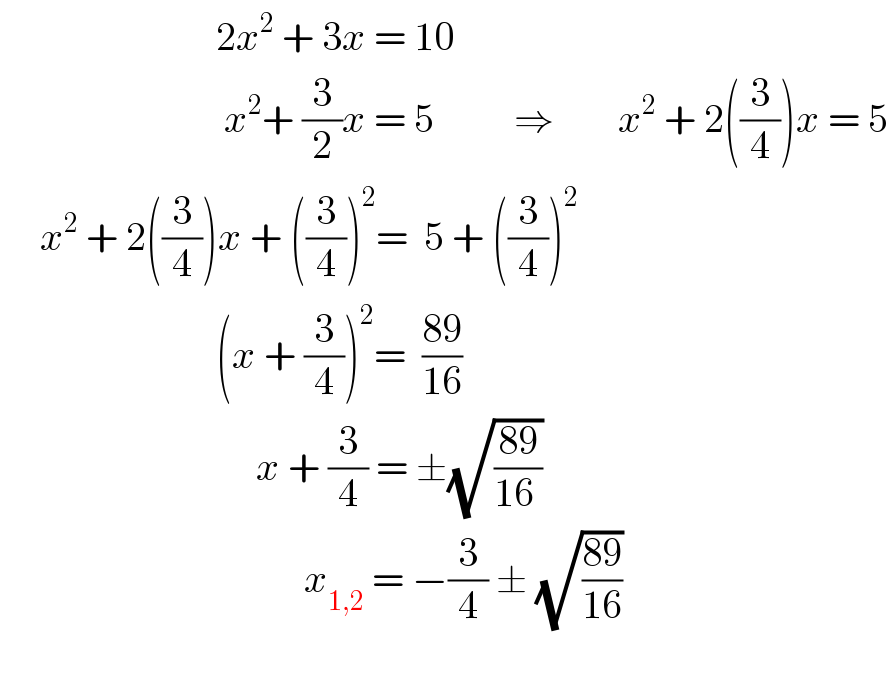
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{x}^{\mathrm{2}} \:+\:\mathrm{3}{x}\:=\:\mathrm{10} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} +\:\frac{\mathrm{3}}{\mathrm{2}}{x}\:=\:\mathrm{5}\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} \:+\:\mathrm{2}\left(\frac{\mathrm{3}}{\mathrm{4}}\right){x}\:=\:\mathrm{5} \\ $$$$\:\:\:\:\:{x}^{\mathrm{2}} \:+\:\mathrm{2}\left(\frac{\mathrm{3}}{\mathrm{4}}\right){x}\:+\:\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} =\:\:\mathrm{5}\:+\:\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({x}\:+\:\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} =\:\:\frac{\mathrm{89}}{\mathrm{16}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\:+\:\frac{\mathrm{3}}{\mathrm{4}}\:=\:\pm\sqrt{\frac{\mathrm{89}}{\mathrm{16}\:}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}_{\mathrm{1},\mathrm{2}} \:=\:−\frac{\mathrm{3}}{\mathrm{4}}\:\pm\:\sqrt{\frac{\mathrm{89}}{\mathrm{16}}} \\ $$$$ \\ $$
Commented by Pk1167156@gmail.com last updated on 06/Dec/18
Nice sir
Commented by afachri last updated on 06/Dec/18

$$\mathrm{thanks}\:\mathrm{Sir} \\ $$
Answered by afachri last updated on 05/Dec/18
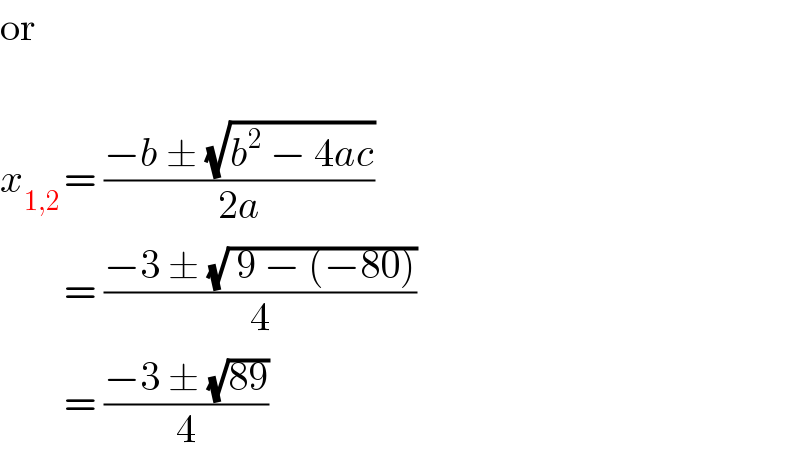
$$\mathrm{or} \\ $$$$ \\ $$$${x}_{\mathrm{1},\mathrm{2}\:} =\:\frac{−{b}\:\pm\:\sqrt{{b}^{\mathrm{2}} \:−\:\mathrm{4}{ac}}}{\mathrm{2}{a}} \\ $$$$\:\:\:\:\:\:\:\:=\:\frac{−\mathrm{3}\:\pm\:\sqrt{\:\mathrm{9}\:−\:\left(−\mathrm{80}\right)}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:=\:\frac{−\mathrm{3}\:\pm\:\sqrt{\mathrm{89}}}{\mathrm{4}} \\ $$
