
Question Number 49020 by ajfour last updated on 01/Dec/18
Commented by ajfour last updated on 01/Dec/18

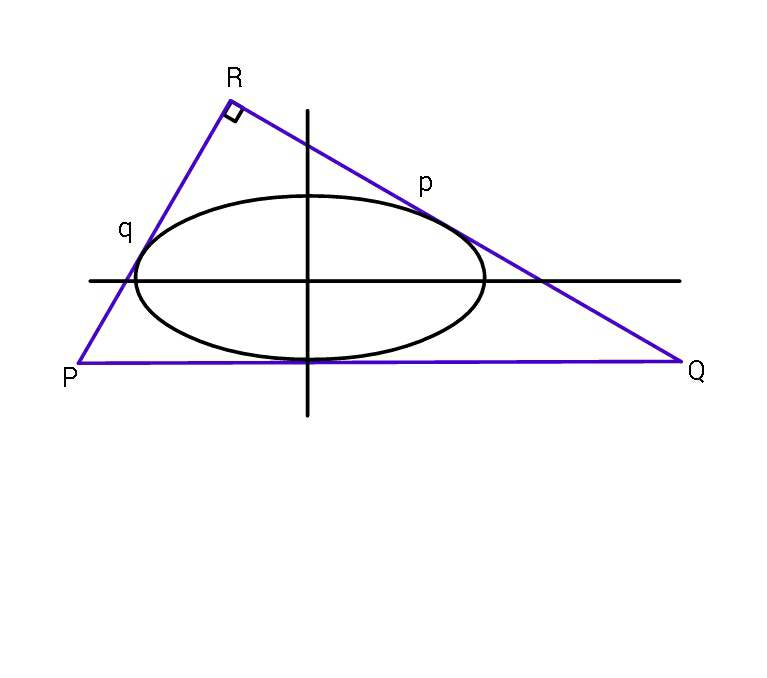
$${If}\:{the}\:{inscribed}\:{ellipse}\:{is}\:{of}\:{maximum} \\ $$$${area}\:{with}\:{its}\:{major}\:{axis}\:{parallel}\:{to} \\ $$$${side}\:{PQ}\:{of}\:\bigtriangleup{PQR}\:{with}\:{PR}\:=\:{q}\:{and} \\ $$$${QR}\:={p}\:,\:{find}\:\boldsymbol{{a}},\:\boldsymbol{{b}}\:{of}\:{the}\:{ellipse}. \\ $$
Commented by ajfour last updated on 01/Dec/18
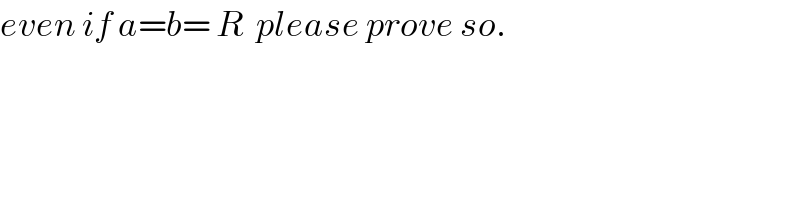
$${even}\:{if}\:{a}={b}=\:{R}\:\:{please}\:{prove}\:{so}. \\ $$
Answered by mr W last updated on 01/Dec/18
Commented by mr W last updated on 02/Dec/18
![let m=(q/p), λ=m^2 −1 R(0,d) where d=((pq)/(√(p^2 +q^2 )))=altitude of triangle M(h,b)=center of ellipse eqn. of ellipse: (((x−h)^2 )/a^2 )+(((y−b)^2 )/b^2 )=1 eqn. of RQ: y=−mx+d a^2 m^2 +b^2 =(d−mh−b)^2 ← tangent of ellipsr a^2 m^2 =(d−mh)^2 −2(d−mh)b a^2 m^2 +2(d−mh)b=(d−mh)^2 ...(i) eqn. of RP: y=(1/m)x+d (a^2 /m^2 )+b^2 =(d+(h/m)−b)^2 ← tangent of ellipse (a^2 /m^2 )=(d+(h/m))^2 −2(d+(h/m))b a^2 =(md+h)^2 −2m(md+h)b a^2 +2m(md+h)b=(md+h)^2 ...(ii) case 1: p=q, i.e. m=1, h=0 from (i) or (ii) we get a^2 +2db=d^2 ⇒b=((d^2 −a^2 )/(2d)) area of ellipse A=πab=((π(d^2 a−a^3 ))/(2d)) (dA/da)=0⇒d^2 −3a^2 =0⇒a=(d/(√3))⇒b=(d/3) case 2: p≠q, i.e. m≠1 (ii)×m^2 −(i): 2[m^4 d+m^3 h−d+mh]b=(m^2 d+mh+d−mh)(m^2 d+mh−d+mh) 2[(m^2 −1)d+mh]b=[(m^2 −1)d+2mh]d ⇒b=(([(m^2 −1)d+2mh]d)/(2[(m^2 −1)d+mh]))=(([(m^2 −1)+((2mh)/d)]d)/(2[(m^2 −1)+((mh)/d)])) ⇒b=(d/2)(((λ+2μ)/(λ+μ))) with μ=((mh)/d)=((h(√(p^2 +q^2 )))/p^2 ) (i)×m(md+h)−(ii)×(d−mh): a^2 [m^3 (md+h)−(d−mh)]=m(md+h)(d−mh)^2 −(d−mh)(md+h)^2 a^2 [(m^2 −1)d+mh]=(mh−d)(md+h)h ⇒a^2 =(((mh−d)(md+h)h)/((m^2 −1)d+mh))=(d^2 /m^2 )×(((((mh)/d)−1)(m^2 +((mh)/d))((mh)/d))/([(m^2 −1)+((mh)/d)])) ⇒a^2 =(d^2 /m^2 )×((μ(μ−1)(m^2 +μ))/(λ+μ)) P=((4m^2 )/d^2 )×a^2 b^2 =((μ(μ−1)(λ+1+μ)(λ+2μ)^2 )/((λ+μ)^3 )) since area of ellipse is A=πab, max. A means also max. P. (dP/dμ)=(((μ−1)(λ+1+μ)(λ+2μ)^2 +μ(λ+1+μ)(λ+2μ)^2 +μ(μ−1)(λ+2μ)^2 +4μ(μ−1)(λ+1+μ)(λ+2μ))/((λ+μ)^3 ))−((3μ(μ−1)(λ+1+μ)(λ+2μ)^2 )/((λ+μ)^4 ))=0 6μ^4 +13λμ^3 +(9λ^2 −2λ−2)μ^2 +(2λ^3 −3λ^2 −3λ)μ−(λ^3 +λ^2 )=2μ^4 +λμ^3 −(λ^2 +2λ+2)μ^2 +(λ^2 +λ)μ ⇒4μ^4 +12λμ^3 +10λ^2 μ^2 +2λ(λ^2 −2λ−2)μ−λ^2 (λ+1)=0 we solve this eqn. for μ=f(λ) ⇒a=(d/m)(√((μ(μ−1)(m^2 +μ))/(m^2 +μ−1))) ⇒b=(d/2)(1+(μ/(m^2 +μ−1))) ⇒h=((μd)/m)=((μp^2 )/(√(p^2 +q^2 )))](Q49047.png)
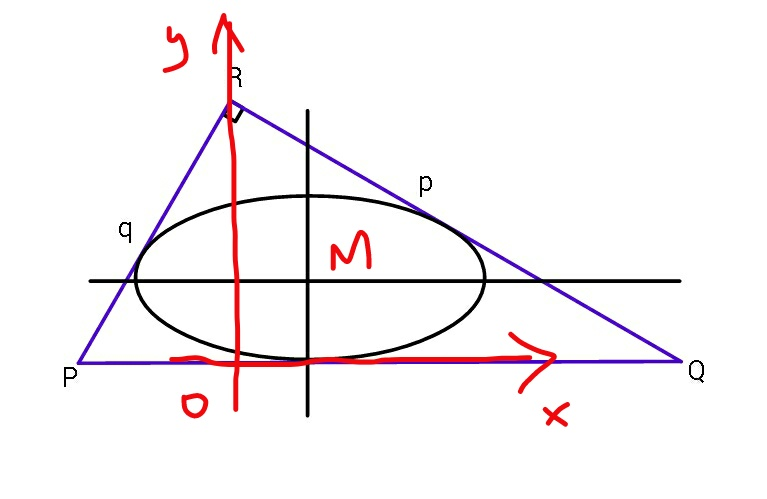
$${let}\:{m}=\frac{{q}}{{p}},\:\lambda={m}^{\mathrm{2}} −\mathrm{1} \\ $$$${R}\left(\mathrm{0},{d}\right) \\ $$$${where}\:{d}=\frac{{pq}}{\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }}={altitude}\:{of}\:{triangle} \\ $$$${M}\left({h},{b}\right)={center}\:{of}\:{ellipse} \\ $$$${eqn}.\:{of}\:{ellipse}: \\ $$$$\frac{\left({x}−{h}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({y}−{b}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$ \\ $$$${eqn}.\:{of}\:{RQ}: \\ $$$${y}=−{mx}+{d} \\ $$$${a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} =\left({d}−{mh}−{b}\right)^{\mathrm{2}} \:\:\leftarrow\:{tangent}\:{of}\:{ellipsr} \\ $$$${a}^{\mathrm{2}} {m}^{\mathrm{2}} =\left({d}−{mh}\right)^{\mathrm{2}} −\mathrm{2}\left({d}−{mh}\right){b} \\ $$$${a}^{\mathrm{2}} {m}^{\mathrm{2}} +\mathrm{2}\left({d}−{mh}\right){b}=\left({d}−{mh}\right)^{\mathrm{2}} \:\:\:...\left({i}\right) \\ $$$$ \\ $$$${eqn}.\:{of}\:{RP}: \\ $$$${y}=\frac{\mathrm{1}}{{m}}{x}+{d} \\ $$$$\frac{{a}^{\mathrm{2}} }{{m}^{\mathrm{2}} }+{b}^{\mathrm{2}} =\left({d}+\frac{{h}}{{m}}−{b}\right)^{\mathrm{2}} \:\leftarrow\:{tangent}\:{of}\:{ellipse} \\ $$$$\frac{{a}^{\mathrm{2}} }{{m}^{\mathrm{2}} }=\left({d}+\frac{{h}}{{m}}\right)^{\mathrm{2}} −\mathrm{2}\left({d}+\frac{{h}}{{m}}\right){b} \\ $$$${a}^{\mathrm{2}} =\left({md}+{h}\right)^{\mathrm{2}} −\mathrm{2}{m}\left({md}+{h}\right){b} \\ $$$${a}^{\mathrm{2}} +\mathrm{2}{m}\left({md}+{h}\right){b}=\left({md}+{h}\right)^{\mathrm{2}} \:\:\:...\left({ii}\right) \\ $$$$ \\ $$$$\boldsymbol{{case}}\:\mathrm{1}:\:{p}={q},\:{i}.{e}.\:{m}=\mathrm{1},\:{h}=\mathrm{0} \\ $$$${from}\:\left({i}\right)\:{or}\:\left({ii}\right)\:{we}\:{get} \\ $$$${a}^{\mathrm{2}} +\mathrm{2}{db}={d}^{\mathrm{2}} \\ $$$$\Rightarrow{b}=\frac{{d}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{d}} \\ $$$${area}\:{of}\:{ellipse}\:{A}=\pi{ab}=\frac{\pi\left({d}^{\mathrm{2}} {a}−{a}^{\mathrm{3}} \right)}{\mathrm{2}{d}} \\ $$$$\frac{{dA}}{{da}}=\mathrm{0}\Rightarrow{d}^{\mathrm{2}} −\mathrm{3}{a}^{\mathrm{2}} =\mathrm{0}\Rightarrow{a}=\frac{{d}}{\sqrt{\mathrm{3}}}\Rightarrow{b}=\frac{{d}}{\mathrm{3}} \\ $$$$ \\ $$$$\boldsymbol{{case}}\:\mathrm{2}:\:{p}\neq{q},\:{i}.{e}.\:{m}\neq\mathrm{1} \\ $$$$\left({ii}\right)×{m}^{\mathrm{2}} −\left({i}\right): \\ $$$$\mathrm{2}\left[{m}^{\mathrm{4}} {d}+{m}^{\mathrm{3}} {h}−{d}+{mh}\right]{b}=\left({m}^{\mathrm{2}} {d}+{mh}+{d}−{mh}\right)\left({m}^{\mathrm{2}} {d}+{mh}−{d}+{mh}\right) \\ $$$$\mathrm{2}\left[\left({m}^{\mathrm{2}} −\mathrm{1}\right){d}+{mh}\right]{b}=\left[\left({m}^{\mathrm{2}} −\mathrm{1}\right){d}+\mathrm{2}{mh}\right]{d} \\ $$$$\Rightarrow{b}=\frac{\left[\left({m}^{\mathrm{2}} −\mathrm{1}\right){d}+\mathrm{2}{mh}\right]{d}}{\mathrm{2}\left[\left({m}^{\mathrm{2}} −\mathrm{1}\right){d}+{mh}\right]}=\frac{\left[\left({m}^{\mathrm{2}} −\mathrm{1}\right)+\frac{\mathrm{2}{mh}}{{d}}\right]{d}}{\mathrm{2}\left[\left({m}^{\mathrm{2}} −\mathrm{1}\right)+\frac{{mh}}{{d}}\right]} \\ $$$$\Rightarrow{b}=\frac{{d}}{\mathrm{2}}\left(\frac{\lambda+\mathrm{2}\mu}{\lambda+\mu}\right)\:{with}\:\mu=\frac{{mh}}{{d}}=\frac{{h}\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }}{{p}^{\mathrm{2}} } \\ $$$$ \\ $$$$\left({i}\right)×{m}\left({md}+{h}\right)−\left({ii}\right)×\left({d}−{mh}\right): \\ $$$${a}^{\mathrm{2}} \left[{m}^{\mathrm{3}} \left({md}+{h}\right)−\left({d}−{mh}\right)\right]={m}\left({md}+{h}\right)\left({d}−{mh}\right)^{\mathrm{2}} −\left({d}−{mh}\right)\left({md}+{h}\right)^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} \left[\left({m}^{\mathrm{2}} −\mathrm{1}\right){d}+{mh}\right]=\left({mh}−{d}\right)\left({md}+{h}\right){h} \\ $$$$\Rightarrow{a}^{\mathrm{2}} =\frac{\left({mh}−{d}\right)\left({md}+{h}\right){h}}{\left({m}^{\mathrm{2}} −\mathrm{1}\right){d}+{mh}}=\frac{{d}^{\mathrm{2}} }{{m}^{\mathrm{2}} }×\frac{\left(\frac{{mh}}{{d}}−\mathrm{1}\right)\left({m}^{\mathrm{2}} +\frac{{mh}}{{d}}\right)\frac{{mh}}{{d}}}{\left[\left({m}^{\mathrm{2}} −\mathrm{1}\right)+\frac{{mh}}{{d}}\right]} \\ $$$$\Rightarrow{a}^{\mathrm{2}} =\frac{{d}^{\mathrm{2}} }{{m}^{\mathrm{2}} }×\frac{\mu\left(\mu−\mathrm{1}\right)\left({m}^{\mathrm{2}} +\mu\right)}{\lambda+\mu} \\ $$$${P}=\frac{\mathrm{4}{m}^{\mathrm{2}} }{{d}^{\mathrm{2}} }×{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\frac{\mu\left(\mu−\mathrm{1}\right)\left(\lambda+\mathrm{1}+\mu\right)\left(\lambda+\mathrm{2}\mu\right)^{\mathrm{2}} }{\left(\lambda+\mu\right)^{\mathrm{3}} } \\ $$$${since}\:{area}\:{of}\:{ellipse}\:{is}\:{A}=\pi{ab},\:{max}.\:{A} \\ $$$${means}\:{also}\:{max}.\:{P}. \\ $$$$\frac{{dP}}{{d}\mu}=\frac{\left(\mu−\mathrm{1}\right)\left(\lambda+\mathrm{1}+\mu\right)\left(\lambda+\mathrm{2}\mu\right)^{\mathrm{2}} +\mu\left(\lambda+\mathrm{1}+\mu\right)\left(\lambda+\mathrm{2}\mu\right)^{\mathrm{2}} +\mu\left(\mu−\mathrm{1}\right)\left(\lambda+\mathrm{2}\mu\right)^{\mathrm{2}} +\mathrm{4}\mu\left(\mu−\mathrm{1}\right)\left(\lambda+\mathrm{1}+\mu\right)\left(\lambda+\mathrm{2}\mu\right)}{\left(\lambda+\mu\right)^{\mathrm{3}} }−\frac{\mathrm{3}\mu\left(\mu−\mathrm{1}\right)\left(\lambda+\mathrm{1}+\mu\right)\left(\lambda+\mathrm{2}\mu\right)^{\mathrm{2}} }{\left(\lambda+\mu\right)^{\mathrm{4}} }=\mathrm{0} \\ $$$$\mathrm{6}\mu^{\mathrm{4}} +\mathrm{13}\lambda\mu^{\mathrm{3}} +\left(\mathrm{9}\lambda^{\mathrm{2}} −\mathrm{2}\lambda−\mathrm{2}\right)\mu^{\mathrm{2}} +\left(\mathrm{2}\lambda^{\mathrm{3}} −\mathrm{3}\lambda^{\mathrm{2}} −\mathrm{3}\lambda\right)\mu−\left(\lambda^{\mathrm{3}} +\lambda^{\mathrm{2}} \right)=\mathrm{2}\mu^{\mathrm{4}} +\lambda\mu^{\mathrm{3}} −\left(\lambda^{\mathrm{2}} +\mathrm{2}\lambda+\mathrm{2}\right)\mu^{\mathrm{2}} +\left(\lambda^{\mathrm{2}} +\lambda\right)\mu \\ $$$$\Rightarrow\mathrm{4}\mu^{\mathrm{4}} +\mathrm{12}\lambda\mu^{\mathrm{3}} +\mathrm{10}\lambda^{\mathrm{2}} \mu^{\mathrm{2}} +\mathrm{2}\lambda\left(\lambda^{\mathrm{2}} −\mathrm{2}\lambda−\mathrm{2}\right)\mu−\lambda^{\mathrm{2}} \left(\lambda+\mathrm{1}\right)=\mathrm{0} \\ $$$${we}\:{solve}\:{this}\:{eqn}.\:{for}\:\mu={f}\left(\lambda\right) \\ $$$$\Rightarrow{a}=\frac{{d}}{{m}}\sqrt{\frac{\mu\left(\mu−\mathrm{1}\right)\left({m}^{\mathrm{2}} +\mu\right)}{{m}^{\mathrm{2}} +\mu−\mathrm{1}}} \\ $$$$\Rightarrow{b}=\frac{{d}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mu}{{m}^{\mathrm{2}} +\mu−\mathrm{1}}\right) \\ $$$$\Rightarrow{h}=\frac{\mu{d}}{{m}}=\frac{\mu{p}^{\mathrm{2}} }{\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }} \\ $$
Commented by ajfour last updated on 02/Dec/18

$${how}\:{can}\:{we}\:{find}\:\:{h}\:\left({the}\:{x}\:{coordinate}\right. \\ $$$${of}\:{the}\:{center}\:{of}\:{ellipse}\:{inscribed} \\ $$$${in}\:{terms}\:{of}\:{a}\:{and}\:{b}\:,\:{Sir}\:? \\ $$
Commented by mr W last updated on 02/Dec/18
Commented by mr W last updated on 02/Dec/18
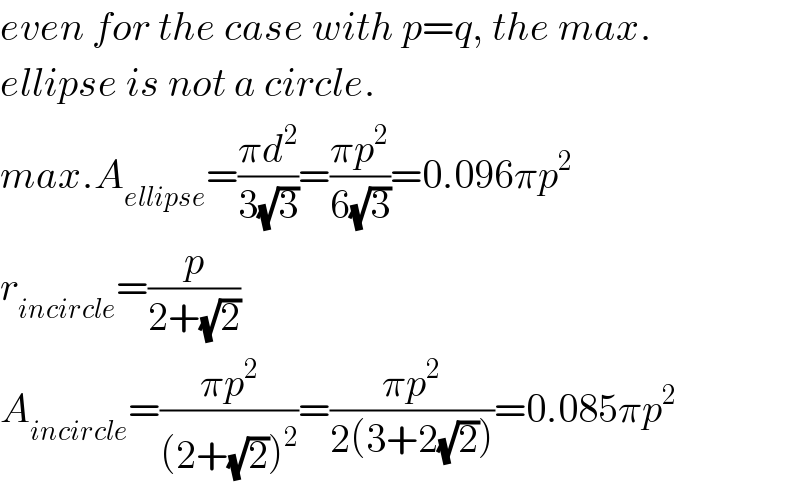
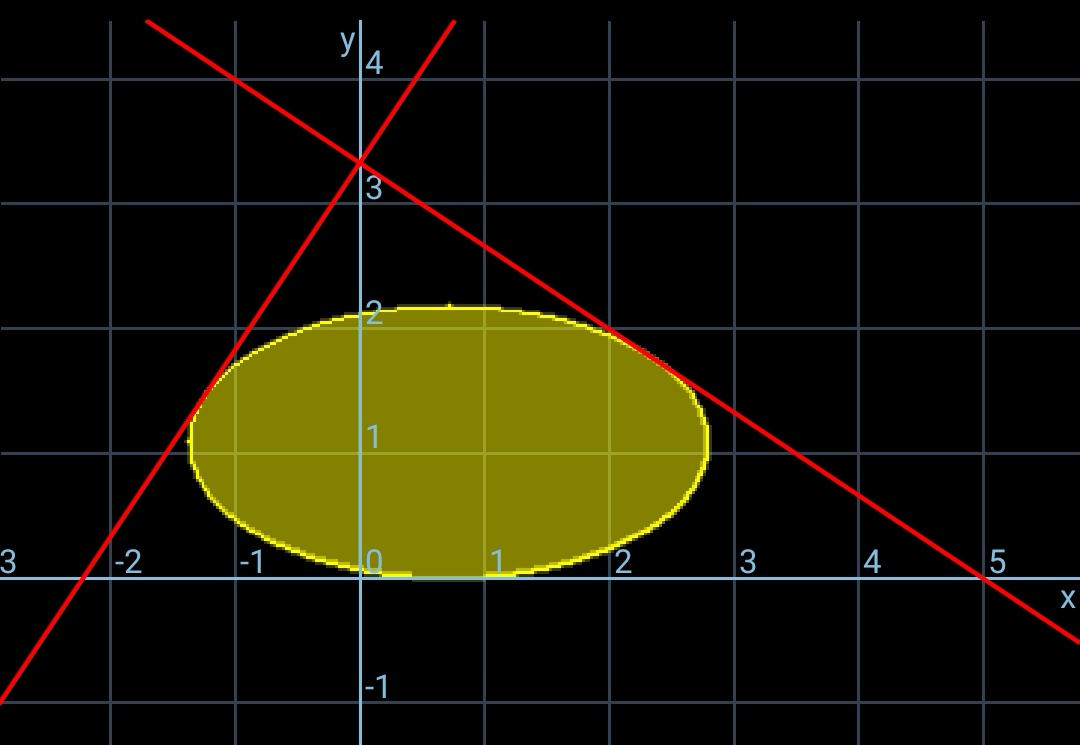
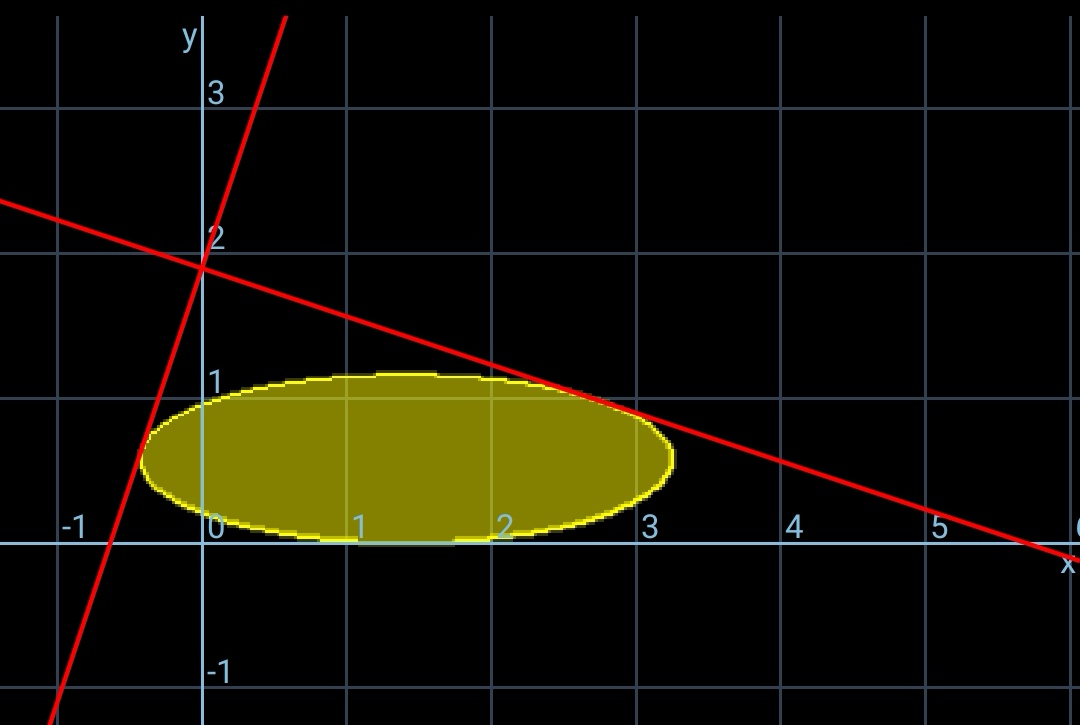
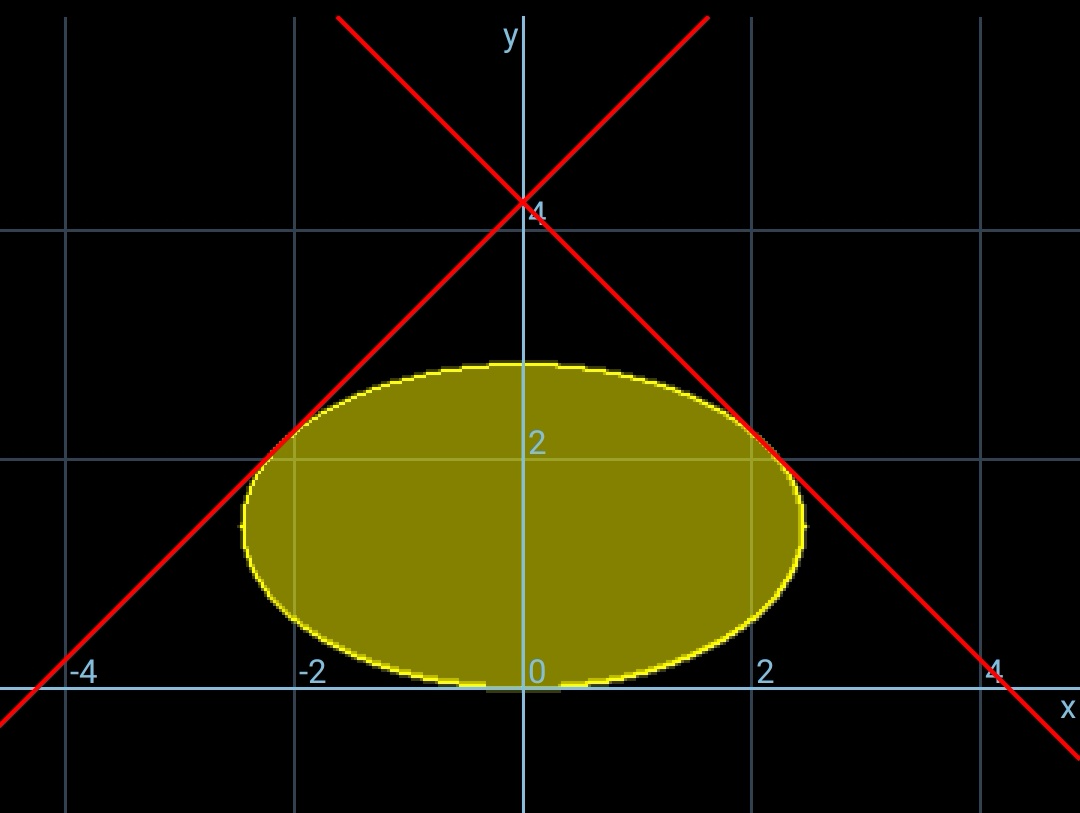
$${even}\:{for}\:{the}\:{case}\:{with}\:{p}={q},\:{the}\:{max}. \\ $$$${ellipse}\:{is}\:{not}\:{a}\:{circle}. \\ $$$${max}.{A}_{{ellipse}} =\frac{\pi{d}^{\mathrm{2}} }{\mathrm{3}\sqrt{\mathrm{3}}}=\frac{\pi{p}^{\mathrm{2}} }{\mathrm{6}\sqrt{\mathrm{3}}}=\mathrm{0}.\mathrm{096}\pi{p}^{\mathrm{2}} \\ $$$${r}_{{incircle}} =\frac{{p}}{\mathrm{2}+\sqrt{\mathrm{2}}} \\ $$$${A}_{{incircle}} =\frac{\pi{p}^{\mathrm{2}} }{\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\pi{p}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)}=\mathrm{0}.\mathrm{085}\pi{p}^{\mathrm{2}} \\ $$
Commented by mr W last updated on 02/Dec/18
Commented by mr W last updated on 02/Dec/18
Commented by mr W last updated on 02/Dec/18
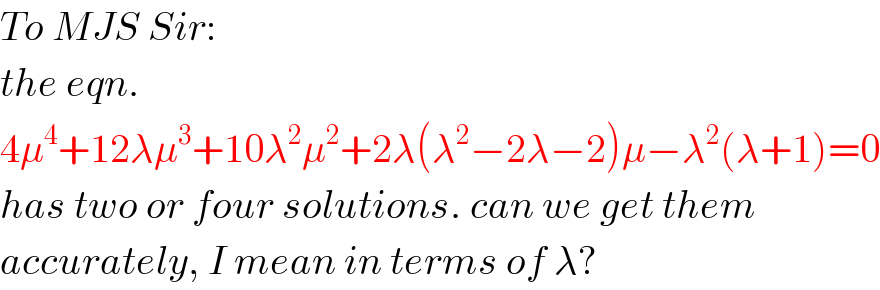
$${To}\:{MJS}\:{Sir}: \\ $$$${the}\:{eqn}. \\ $$$$\mathrm{4}\mu^{\mathrm{4}} +\mathrm{12}\lambda\mu^{\mathrm{3}} +\mathrm{10}\lambda^{\mathrm{2}} \mu^{\mathrm{2}} +\mathrm{2}\lambda\left(\lambda^{\mathrm{2}} −\mathrm{2}\lambda−\mathrm{2}\right)\mu−\lambda^{\mathrm{2}} \left(\lambda+\mathrm{1}\right)=\mathrm{0} \\ $$$${has}\:{two}\:{or}\:{four}\:{solutions}.\:{can}\:{we}\:{get}\:{them} \\ $$$${accurately},\:{I}\:{mean}\:{in}\:{terms}\:{of}\:\lambda? \\ $$
Commented by ajfour last updated on 02/Dec/18

$${Very}\:{Great},\:{Sir}!\:{you}\:{make}\:{me} \\ $$$${very}\:{happy},\:{my}\:{mind}'{s}\:{eye}\:{rightaway}\: \\ $$$${said},\:{it}\:{should}\:{be}\:{so}.\left({more}\:{space}\right. \\ $$$$\left.{downwards}..\right) \\ $$$${Thank}\:{you}\:{sir}!\: \\ $$
Commented by mr W last updated on 02/Dec/18
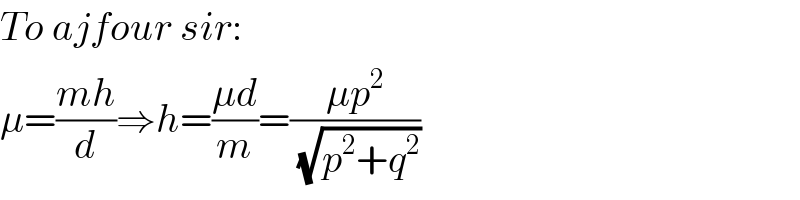
$${To}\:{ajfour}\:{sir}: \\ $$$$\mu=\frac{{mh}}{{d}}\Rightarrow{h}=\frac{\mu{d}}{{m}}=\frac{\mu{p}^{\mathrm{2}} }{\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }} \\ $$
Commented by mr W last updated on 02/Dec/18
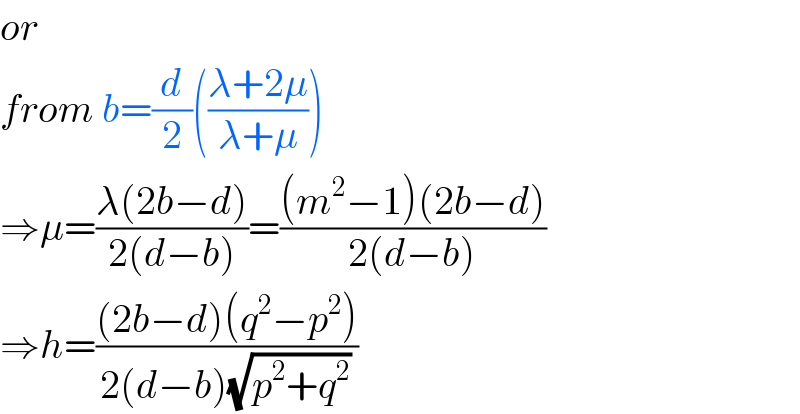
$${or} \\ $$$${from}\:{b}=\frac{{d}}{\mathrm{2}}\left(\frac{\lambda+\mathrm{2}\mu}{\lambda+\mu}\right) \\ $$$$\Rightarrow\mu=\frac{\lambda\left(\mathrm{2}{b}−{d}\right)}{\mathrm{2}\left({d}−{b}\right)}=\frac{\left({m}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{2}{b}−{d}\right)}{\mathrm{2}\left({d}−{b}\right)} \\ $$$$\Rightarrow{h}=\frac{\left(\mathrm{2}{b}−{d}\right)\left({q}^{\mathrm{2}} −{p}^{\mathrm{2}} \right)}{\mathrm{2}\left({d}−{b}\right)\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }} \\ $$
Commented by MJS last updated on 02/Dec/18
$$\mathrm{sorry}\:\mathrm{just}\:\mathrm{read}\:\mathrm{this},\:\mathrm{I}'\mathrm{ll}\:\mathrm{try}\:\mathrm{later} \\ $$
Commented by MJS last updated on 02/Dec/18
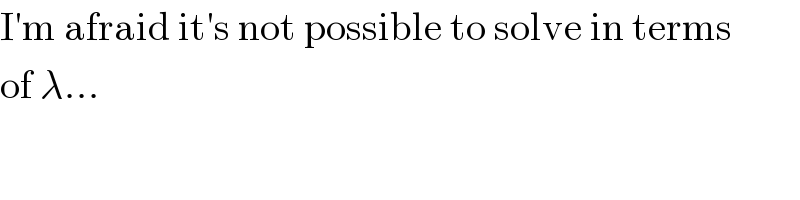
$$\mathrm{I}'\mathrm{m}\:\mathrm{afraid}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{in}\:\mathrm{terms} \\ $$$$\mathrm{of}\:\lambda... \\ $$
Commented by mr W last updated on 03/Dec/18
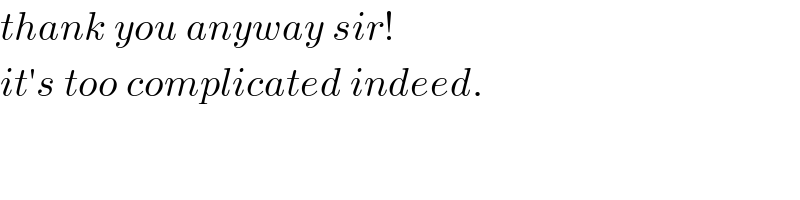
$${thank}\:{you}\:{anyway}\:{sir}! \\ $$$${it}'{s}\:{too}\:{complicated}\:{indeed}. \\ $$
Answered by ajfour last updated on 03/Dec/18
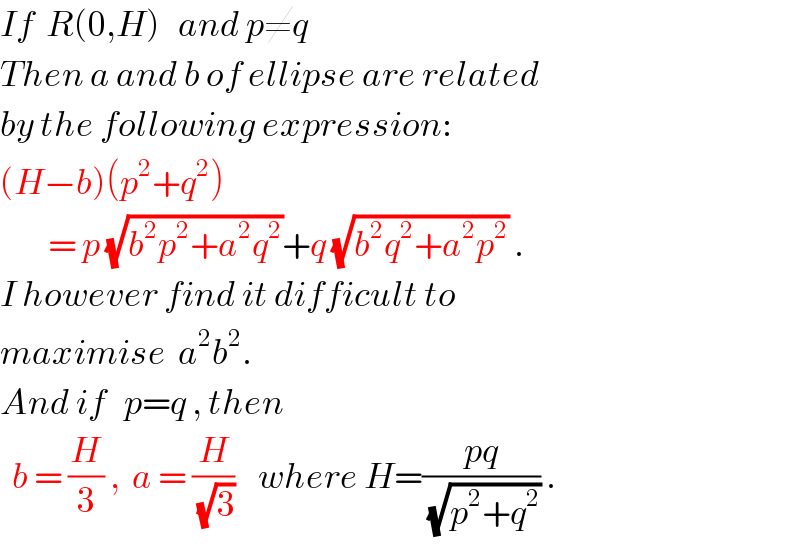
$${If}\:\:{R}\left(\mathrm{0},{H}\right)\:\:\:{and}\:{p}\neq{q} \\ $$$${Then}\:{a}\:{and}\:{b}\:{of}\:{ellipse}\:{are}\:{related} \\ $$$${by}\:{the}\:{following}\:{expression}: \\ $$$$\left({H}−{b}\right)\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:=\:{p}\:\sqrt{{b}^{\mathrm{2}} {p}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} }+{q}\:\sqrt{{b}^{\mathrm{2}} {q}^{\mathrm{2}} +{a}^{\mathrm{2}} {p}^{\mathrm{2}} }\:. \\ $$$${I}\:{however}\:{find}\:{it}\:{difficult}\:{to} \\ $$$${maximise}\:\:{a}^{\mathrm{2}} {b}^{\mathrm{2}} . \\ $$$${And}\:{if}\:\:\:{p}={q}\:,\:{then} \\ $$$$\:\:{b}\:=\:\frac{{H}}{\mathrm{3}}\:,\:\:{a}\:=\:\frac{{H}}{\sqrt{\mathrm{3}}}\:\:\:\:{where}\:{H}=\frac{{pq}}{\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }}\:. \\ $$
Commented by mr W last updated on 03/Dec/18
![(H−b)(p^2 +q^2 )= p (√(b^2 p^2 +a^2 q^2 ))+q (√(b^2 q^2 +a^2 p^2 )) (aH−ab)(p^2 +q^2 )= p (√(a^2 b^2 p^2 +a^4 q^2 ))+q (√(a^2 b^2 q^2 +a^4 p^2 )) (aH−S)(p^2 +q^2 )= p (√(S^2 p^2 +a^4 q^2 ))+q (√(S^2 q^2 +a^4 p^2 )) with S=ab (dS/da)=0 H(p^2 +q^2 )= p ((4a^3 q^2 )/(2(√(S^2 p^2 +a^4 q^2 ))))+q((4a^3 p^2 )/(2 (√(S^2 q^2 +a^4 p^2 )) )) H(p^2 +q^2 )=2pqa^2 [ (q/(√(b^2 p^2 +a^2 q^2 )))+(p/( (√(b^2 q^2 +a^2 p^2 )) ))] H(p^2 +q^2 )=2pqa^2 [ ((q (√(b^2 q^2 +a^2 p^2 ))+p(√(b^2 p^2 +a^2 q^2 )))/(√((b^2 p^2 +a^2 q^2 )(b^2 q^2 +a^2 p^2 ))))] H(p^2 +q^2 )=2pqa^2 [ (((H−b)(p^2 +q^2 ))/(√((b^2 p^2 +a^2 q^2 )(b^2 q^2 +a^2 p^2 ))))] H=2pqa^2 [ (((H−b))/(√((b^2 p^2 +a^2 q^2 )(b^2 q^2 +a^2 p^2 ))))] let β=(b/a) ((pq)/(√(p^2 +q^2 )))=2pq[ (((H−b))/(√((β^2 p^2 +q^2 )(β^2 q^2 +p^2 ))))] (1/(√(p^2 +q^2 )))=2[ (((H−b))/(√((β^2 p^2 +q^2 )(β^2 q^2 +p^2 ))))] b=H[1−(1/(2H))(√(((β^2 p^2 +q^2 )(β^2 q^2 +p^2 ))/(p^2 +q^2 )))] (H/b)=(1/([1−(1/(2H))(√(((β^2 p^2 +q^2 )(β^2 q^2 +p^2 ))/(p^2 +q^2 )))])) =(1/(1−((√((β^2 p^2 +q^2 )(β^2 q^2 +p^2 )))/(2pq)))) ((H/b)−1)(p^2 +q^2 )β= p (√(β^2 p^2 +q^2 ))+q (√(β^2 q^2 +p^2 )) {(1/(1−((√((β^2 p^2 +q^2 )(β^2 q^2 +p^2 )))/(2pq))))−1}(p^2 +q^2 )β= p (√(β^2 p^2 +q^2 ))+q (√(β^2 q^2 +p^2 )) with m=(q/p) ⇒{(1/(1−((√((β^2 +m^2 )(β^2 m^2 +1)))/2)))−1}(1+m^2 )β= (√(β^2 +m^2 ))+m (√(β^2 m^2 +1)) ⇒β=....](Q49135.png)
$$\left({H}−{b}\right)\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)=\:{p}\:\sqrt{{b}^{\mathrm{2}} {p}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} }+{q}\:\sqrt{{b}^{\mathrm{2}} {q}^{\mathrm{2}} +{a}^{\mathrm{2}} {p}^{\mathrm{2}} }\: \\ $$$$\left({aH}−{ab}\right)\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)=\:{p}\:\sqrt{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {p}^{\mathrm{2}} +{a}^{\mathrm{4}} {q}^{\mathrm{2}} }+{q}\:\sqrt{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {q}^{\mathrm{2}} +{a}^{\mathrm{4}} {p}^{\mathrm{2}} }\: \\ $$$$\left({aH}−{S}\right)\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)=\:{p}\:\sqrt{{S}^{\mathrm{2}} {p}^{\mathrm{2}} +{a}^{\mathrm{4}} {q}^{\mathrm{2}} }+{q}\:\sqrt{{S}^{\mathrm{2}} {q}^{\mathrm{2}} +{a}^{\mathrm{4}} {p}^{\mathrm{2}} }\: \\ $$$${with}\:{S}={ab} \\ $$$$\frac{{dS}}{{da}}=\mathrm{0} \\ $$$${H}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)=\:{p}\:\frac{\mathrm{4}{a}^{\mathrm{3}} {q}^{\mathrm{2}} }{\mathrm{2}\sqrt{{S}^{\mathrm{2}} {p}^{\mathrm{2}} +{a}^{\mathrm{4}} {q}^{\mathrm{2}} }}+{q}\frac{\mathrm{4}{a}^{\mathrm{3}} {p}^{\mathrm{2}} }{\mathrm{2}\:\sqrt{{S}^{\mathrm{2}} {q}^{\mathrm{2}} +{a}^{\mathrm{4}} {p}^{\mathrm{2}} }\:} \\ $$$${H}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)=\mathrm{2}{pqa}^{\mathrm{2}} \left[\:\frac{{q}}{\sqrt{{b}^{\mathrm{2}} {p}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} }}+\frac{{p}}{\:\sqrt{{b}^{\mathrm{2}} {q}^{\mathrm{2}} +{a}^{\mathrm{2}} {p}^{\mathrm{2}} }\:}\right] \\ $$$${H}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)=\mathrm{2}{pqa}^{\mathrm{2}} \left[\:\frac{{q}\:\sqrt{{b}^{\mathrm{2}} {q}^{\mathrm{2}} +{a}^{\mathrm{2}} {p}^{\mathrm{2}} }+{p}\sqrt{{b}^{\mathrm{2}} {p}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} }}{\sqrt{\left({b}^{\mathrm{2}} {p}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} {q}^{\mathrm{2}} +{a}^{\mathrm{2}} {p}^{\mathrm{2}} \right)}}\right] \\ $$$${H}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)=\mathrm{2}{pqa}^{\mathrm{2}} \left[\:\frac{\left({H}−{b}\right)\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)}{\sqrt{\left({b}^{\mathrm{2}} {p}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} {q}^{\mathrm{2}} +{a}^{\mathrm{2}} {p}^{\mathrm{2}} \right)}}\right] \\ $$$${H}=\mathrm{2}{pqa}^{\mathrm{2}} \left[\:\frac{\left({H}−{b}\right)}{\sqrt{\left({b}^{\mathrm{2}} {p}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} {q}^{\mathrm{2}} +{a}^{\mathrm{2}} {p}^{\mathrm{2}} \right)}}\right] \\ $$$${let}\:\beta=\frac{{b}}{{a}} \\ $$$$\frac{{pq}}{\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }}=\mathrm{2}{pq}\left[\:\frac{\left({H}−{b}\right)}{\sqrt{\left(\beta^{\mathrm{2}} {p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\left(\beta^{\mathrm{2}} {q}^{\mathrm{2}} +{p}^{\mathrm{2}} \right)}}\right] \\ $$$$\frac{\mathrm{1}}{\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }}=\mathrm{2}\left[\:\frac{\left({H}−{b}\right)}{\sqrt{\left(\beta^{\mathrm{2}} {p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\left(\beta^{\mathrm{2}} {q}^{\mathrm{2}} +{p}^{\mathrm{2}} \right)}}\right] \\ $$$${b}={H}\left[\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{H}}\sqrt{\frac{\left(\beta^{\mathrm{2}} {p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\left(\beta^{\mathrm{2}} {q}^{\mathrm{2}} +{p}^{\mathrm{2}} \right)}{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }}\right] \\ $$$$\frac{{H}}{{b}}=\frac{\mathrm{1}}{\left[\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{H}}\sqrt{\frac{\left(\beta^{\mathrm{2}} {p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\left(\beta^{\mathrm{2}} {q}^{\mathrm{2}} +{p}^{\mathrm{2}} \right)}{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }}\right]} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−\frac{\sqrt{\left(\beta^{\mathrm{2}} {p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\left(\beta^{\mathrm{2}} {q}^{\mathrm{2}} +{p}^{\mathrm{2}} \right)}}{\mathrm{2}{pq}}} \\ $$$$ \\ $$$$\left(\frac{{H}}{{b}}−\mathrm{1}\right)\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\beta=\:{p}\:\sqrt{\beta^{\mathrm{2}} {p}^{\mathrm{2}} +{q}^{\mathrm{2}} }+{q}\:\sqrt{\beta^{\mathrm{2}} {q}^{\mathrm{2}} +{p}^{\mathrm{2}} }\: \\ $$$$\left\{\frac{\mathrm{1}}{\mathrm{1}−\frac{\sqrt{\left(\beta^{\mathrm{2}} {p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\left(\beta^{\mathrm{2}} {q}^{\mathrm{2}} +{p}^{\mathrm{2}} \right)}}{\mathrm{2}{pq}}}−\mathrm{1}\right\}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\beta=\:{p}\:\sqrt{\beta^{\mathrm{2}} {p}^{\mathrm{2}} +{q}^{\mathrm{2}} }+{q}\:\sqrt{\beta^{\mathrm{2}} {q}^{\mathrm{2}} +{p}^{\mathrm{2}} }\: \\ $$$${with}\:{m}=\frac{{q}}{{p}} \\ $$$$\Rightarrow\left\{\frac{\mathrm{1}}{\mathrm{1}−\frac{\sqrt{\left(\beta^{\mathrm{2}} +{m}^{\mathrm{2}} \right)\left(\beta^{\mathrm{2}} {m}^{\mathrm{2}} +\mathrm{1}\right)}}{\mathrm{2}}}−\mathrm{1}\right\}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\beta=\:\:\sqrt{\beta^{\mathrm{2}} +{m}^{\mathrm{2}} }+{m}\:\sqrt{\beta^{\mathrm{2}} {m}^{\mathrm{2}} +\mathrm{1}}\: \\ $$$$\Rightarrow\beta=.... \\ $$
Commented by mr W last updated on 03/Dec/18

$${sir},\:{I}\:{changed}\:{your}\:``−''\:{sign}\:{to}\:``+''\:{without} \\ $$$${to}\:{know}\:{if}\:{it}\:{is}\:{correct}.\:{due}\:{to}\:{symmetry} \\ $$$${I}\:{think}\:{it}\:{should}\:{be}\:``+'',\:{because}\:{the} \\ $$$${result}\:{should}\:{be}\:{unchanged}\:{if}\:{we}\: \\ $$$${exchange}\:{p}\:{and}\:{q}. \\ $$
Commented by ajfour last updated on 03/Dec/18
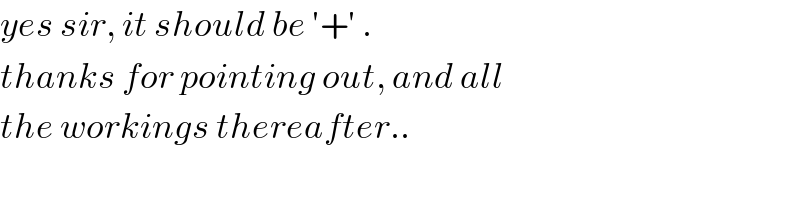
$${yes}\:{sir},\:{it}\:{should}\:{be}\:'+'\:. \\ $$$${thanks}\:{for}\:{pointing}\:{out},\:{and}\:{all} \\ $$$${the}\:{workings}\:{thereafter}.. \\ $$
