
Question Number 48874 by [email protected] last updated on 29/Nov/18
Commented by [email protected] last updated on 29/Nov/18
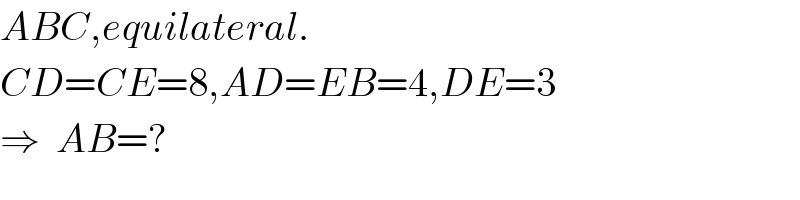
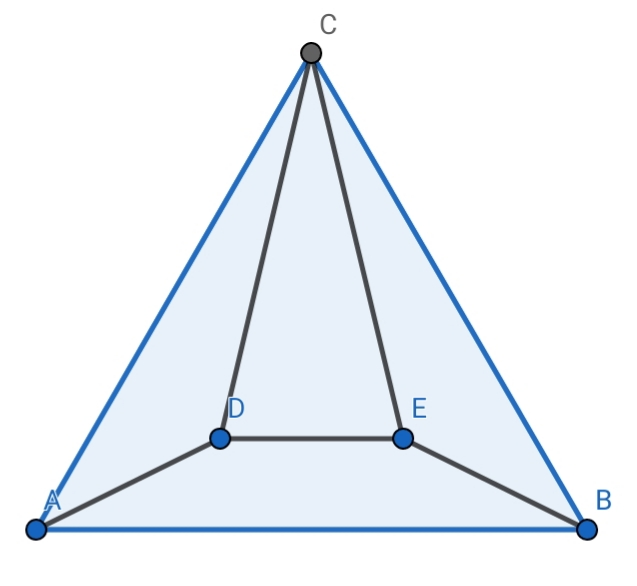
$${ABC},{equilateral}. \\ $$$${CD}={CE}=\mathrm{8},{AD}={EB}=\mathrm{4},{DE}=\mathrm{3} \\ $$$$\Rightarrow\:\:{AB}=? \\ $$
Answered by mr W last updated on 29/Nov/18
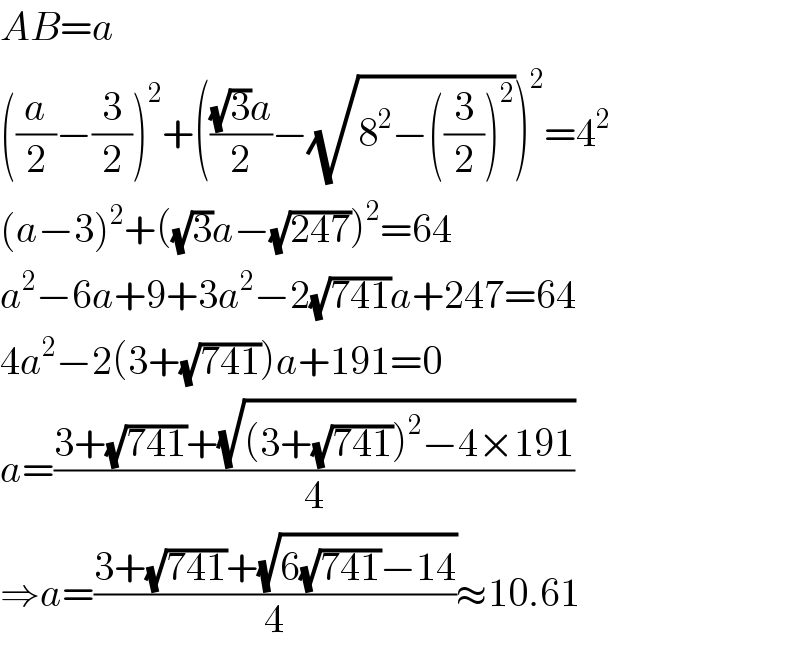
$${AB}={a} \\ $$$$\left(\frac{{a}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}−\sqrt{\mathrm{8}^{\mathrm{2}} −\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} }\right)^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} \\ $$$$\left({a}−\mathrm{3}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}{a}−\sqrt{\mathrm{247}}\right)^{\mathrm{2}} =\mathrm{64} \\ $$$${a}^{\mathrm{2}} −\mathrm{6}{a}+\mathrm{9}+\mathrm{3}{a}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{741}}{a}+\mathrm{247}=\mathrm{64} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{3}+\sqrt{\mathrm{741}}\right){a}+\mathrm{191}=\mathrm{0} \\ $$$${a}=\frac{\mathrm{3}+\sqrt{\mathrm{741}}+\sqrt{\left(\mathrm{3}+\sqrt{\mathrm{741}}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{191}}}{\mathrm{4}} \\ $$$$\Rightarrow{a}=\frac{\mathrm{3}+\sqrt{\mathrm{741}}+\sqrt{\mathrm{6}\sqrt{\mathrm{741}}−\mathrm{14}}}{\mathrm{4}}\approx\mathrm{10}.\mathrm{61} \\ $$
Commented by [email protected] last updated on 29/Nov/18
$${right}\:{answer}\:{dear}\:{mr}\:{w}.{thanks}. \\ $$
Answered by [email protected] last updated on 29/Nov/18

