Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 48540 by behi83417@gmail.com last updated on 25/Nov/18

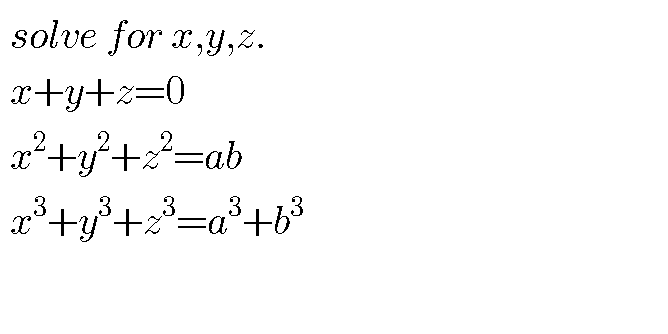
Answered by ajfour last updated on 25/Nov/18

x^2 +y^2 +z^2 +2(xy+yz+zx)=0 ⇒ xy+yz+zx = −((ab)/2) (x+y+z)^3 = x^3 +y^3 +z^3 +3(y+z)x^2 +3(z+x)y^2 +3(x+y)z^3 +6xyz now since x+y+z = 0, ⇒ 0 = −2Σx^3 +6xyz ⇒ xyz = ((a^3 +b^3 )/3) ⇒ x, y, z are roots of eq. t^3 −((ab)/2) t−(((a^3 +b^3 ))/3) = 0 Trigonometric solution to the above cubic gives x,y,and z.

$$\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:+\mathrm{2}\left({xy}+{yz}+{zx}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{xy}+{yz}+{zx}\:=\:−\frac{{ab}}{\mathrm{2}} \\ $$$$\left({x}+{y}+{z}\right)^{\mathrm{3}} \:=\:{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} +\mathrm{3}\left({y}+{z}\right){x}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{3}\left({z}+{x}\right){y}^{\mathrm{2}} +\mathrm{3}\left({x}+{y}\right){z}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{6}{xyz} \\ $$$${now}\:{since}\:\:{x}+{y}+{z}\:=\:\mathrm{0}, \\ $$$$\Rightarrow\:\mathrm{0}\:=\:−\mathrm{2}\Sigma{x}^{\mathrm{3}} +\mathrm{6}{xyz} \\ $$$$\Rightarrow\:\:\:{xyz}\:=\:\frac{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\Rightarrow\:\:{x},\:{y},\:{z}\:{are}\:{roots}\:{of}\:{eq}. \\ $$$$\:\:\:\:\:{t}^{\mathrm{3}} −\frac{{ab}}{\mathrm{2}}\:{t}−\frac{\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} \right)}{\mathrm{3}}\:=\:\mathrm{0} \\ $$$$\:\:{Trigonometric}\:{solution}\:{to}\:{the} \\ $$$${above}\:{cubic}\:{gives}\:\:{x},{y},{and}\:{z}. \\ $$

Commented by behi83417@gmail.com last updated on 25/Nov/18

thank you so much sir Ajfour.but still waiting for another question....

$${thank}\:{you}\:{so}\:{much}\:{sir}\:{Ajfour}.{but} \\ $$$${still}\:{waiting}\:{for}\:{another}\:{question}.... \\ $$

Commented by MJS last updated on 25/Nov/18

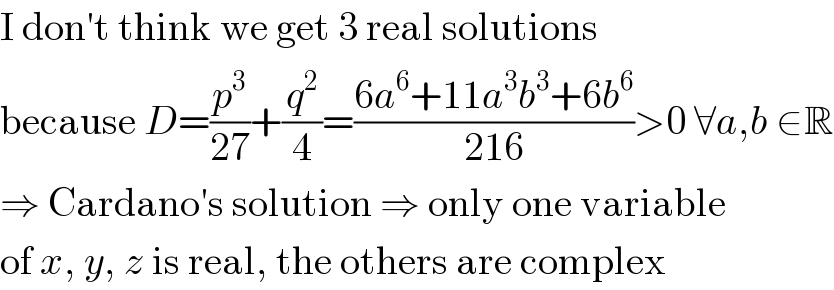
I don′t think we get 3 real solutions because D=(p^3 /(27))+(q^2 /4)=((6a^6 +11a^3 b^3 +6b^6 )/(216))>0 ∀a,b ∈R ⇒ Cardano′s solution ⇒ only one variable of x, y, z is real, the others are complex

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{we}\:\mathrm{get}\:\mathrm{3}\:\mathrm{real}\:\mathrm{solutions} \\ $$$$\mathrm{because}\:{D}=\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}=\frac{\mathrm{6}{a}^{\mathrm{6}} +\mathrm{11}{a}^{\mathrm{3}} {b}^{\mathrm{3}} +\mathrm{6}{b}^{\mathrm{6}} }{\mathrm{216}}>\mathrm{0}\:\forall{a},{b}\:\in\mathbb{R} \\ $$$$\Rightarrow\:\mathrm{Cardano}'\mathrm{s}\:\mathrm{solution}\:\Rightarrow\:\mathrm{only}\:\mathrm{one}\:\mathrm{variable} \\ $$$$\mathrm{of}\:{x},\:{y},\:{z}\:\mathrm{is}\:\mathrm{real},\:\mathrm{the}\:\mathrm{others}\:\mathrm{are}\:\mathrm{complex} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 25/Nov/18

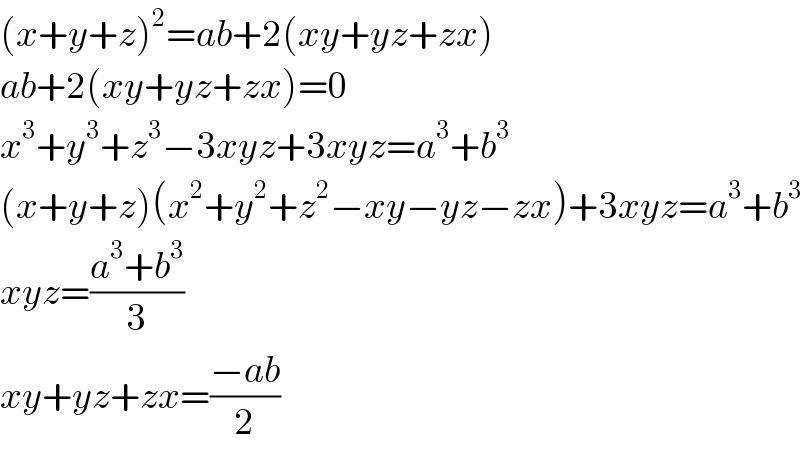
(x+y+z)^2 =ab+2(xy+yz+zx) ab+2(xy+yz+zx)=0 x^3 +y^3 +z^3 −3xyz+3xyz=a^3 +b^3 (x+y+z)(x^2 +y^2 +z^2 −xy−yz−zx)+3xyz=a^3 +b^3 xyz=((a^3 +b^3 )/3) xy+yz+zx=((−ab)/2)

$$\left({x}+{y}+{z}\right)^{\mathrm{2}} ={ab}+\mathrm{2}\left({xy}+{yz}+{zx}\right) \\ $$$${ab}+\mathrm{2}\left({xy}+{yz}+{zx}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} −\mathrm{3}{xyz}+\mathrm{3}{xyz}={a}^{\mathrm{3}} +{b}^{\mathrm{3}} \\ $$$$\left({x}+{y}+{z}\right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} −{xy}−{yz}−{zx}\right)+\mathrm{3}{xyz}={a}^{\mathrm{3}} +{b}^{\mathrm{3}} \\ $$$${xyz}=\frac{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} }{\mathrm{3}} \\ $$$${xy}+{yz}+{zx}=\frac{−{ab}}{\mathrm{2}} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 25/Nov/18

wait pls

$${wait}\:{pls} \\ $$

Commented by behi83417@gmail.com last updated on 25/Nov/18

thank you very much sir tanmay.waiting.....

$${thank}\:{you}\:{very}\:{much}\:{sir}\:{tanmay}.{waiting}..... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com