
Question Number 48522 by ajfour last updated on 25/Nov/18
Commented by ajfour last updated on 25/Nov/18

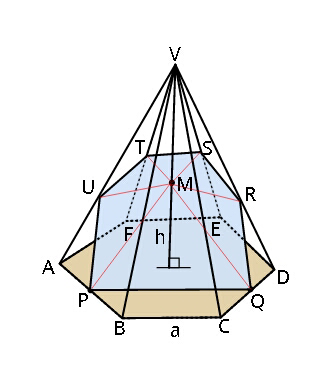
$${A}\:{regular}\:{hexagonal}\:{pyramid} \\ $$$${with}\:{base}\:{edge}\:\boldsymbol{{a}}\:{and}\:{altitude}\:\boldsymbol{{h}}. \\ $$$${Find}\:{the}\:{area}\:{of}\:{a}\:{section}\:{that} \\ $$$${passes}\:{through}\:{midpoints}\:{P},\:{Q} \\ $$$${of}\:{sides}\:{AB}\:{and}\:{CD}\:{and}\:{also} \\ $$$${through}\:{M}\:,\:{the}\:{midpoint}\:{of} \\ $$$${altitude}. \\ $$
Answered by mr W last updated on 25/Nov/18
Commented by mr W last updated on 25/Nov/18
![AD=2a b_1 =PQ=(a+2a)/2=3a/2 b_2 =UR=AD/2=a c=(√(((√3)a/4)^2 +(h/2)^2 ))=((√(3a^2 +4h^2 )))/4 (e/(f−h/2))=(((√3)a/4)/(h/2)) (e/(h−f))=(((√3)a/2)/h) ⇒f−h/2=h−f ⇒f=3h/4 b_3 =ST (b_3 /a)=((h−f)/h)=1/4 ⇒b_3 =a/4 ((d+c)/c)=(f/(h/2))=(3/2) (d/c)=(1/2) ⇒d=c/2=((√(3a^2 +4h^2 )))/8 Area of PQRSTUP=A A=(b_1 +b_2 )c/2+(b_2 +b_3 )d/2=[b_1 c+b_2 (c+d)+b_3 d]/2 =(1/2)[((3a)/2)×((√(3a^2 +4h^2 ))/4)+a×((3(√(3a^2 +4h^2 )))/8)+(a/4)×((√(3a^2 +4h^2 ))/8)] ⇒A=((25a(√(3a^2 +4h^2 )))/(64))](Q48575.png)
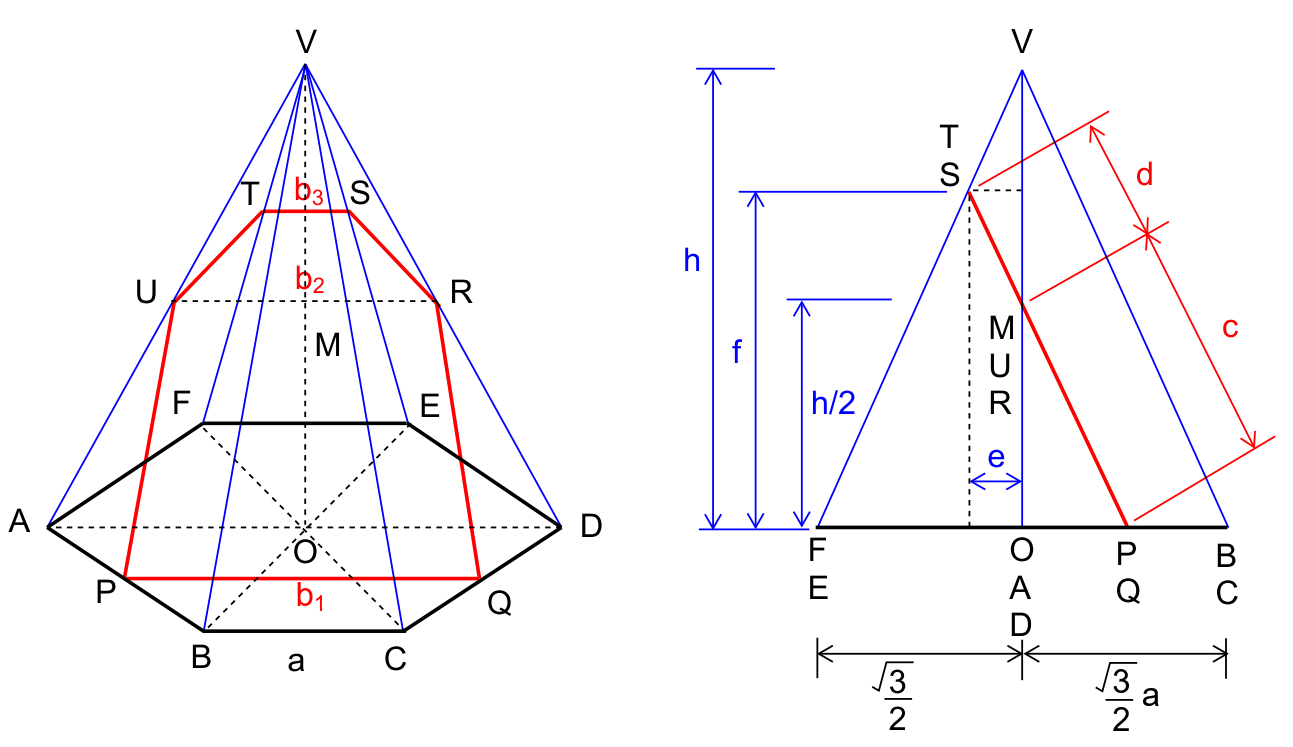
$${AD}=\mathrm{2}{a} \\ $$$${b}_{\mathrm{1}} ={PQ}=\left({a}+\mathrm{2}{a}\right)/\mathrm{2}=\mathrm{3}{a}/\mathrm{2} \\ $$$${b}_{\mathrm{2}} ={UR}={AD}/\mathrm{2}={a} \\ $$$${c}=\sqrt{\left(\sqrt{\mathrm{3}}{a}/\mathrm{4}\right)^{\mathrm{2}} +\left({h}/\mathrm{2}\right)^{\mathrm{2}} }=\left(\sqrt{\mathrm{3}{a}^{\mathrm{2}} +\mathrm{4}{h}^{\mathrm{2}} }\right)/\mathrm{4} \\ $$$$\frac{{e}}{{f}−{h}/\mathrm{2}}=\frac{\sqrt{\mathrm{3}}{a}/\mathrm{4}}{{h}/\mathrm{2}} \\ $$$$\frac{{e}}{{h}−{f}}=\frac{\sqrt{\mathrm{3}}{a}/\mathrm{2}}{{h}} \\ $$$$\Rightarrow{f}−{h}/\mathrm{2}={h}−{f} \\ $$$$\Rightarrow{f}=\mathrm{3}{h}/\mathrm{4} \\ $$$${b}_{\mathrm{3}} ={ST} \\ $$$$\frac{{b}_{\mathrm{3}} }{{a}}=\frac{{h}−{f}}{{h}}=\mathrm{1}/\mathrm{4} \\ $$$$\Rightarrow{b}_{\mathrm{3}} ={a}/\mathrm{4} \\ $$$$\frac{{d}+{c}}{{c}}=\frac{{f}}{{h}/\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\frac{{d}}{{c}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{d}={c}/\mathrm{2}=\left(\sqrt{\mathrm{3}{a}^{\mathrm{2}} +\mathrm{4}{h}^{\mathrm{2}} }\right)/\mathrm{8} \\ $$$${Area}\:{of}\:{PQRSTUP}={A} \\ $$$${A}=\left({b}_{\mathrm{1}} +{b}_{\mathrm{2}} \right){c}/\mathrm{2}+\left({b}_{\mathrm{2}} +{b}_{\mathrm{3}} \right){d}/\mathrm{2}=\left[{b}_{\mathrm{1}} {c}+{b}_{\mathrm{2}} \left({c}+{d}\right)+{b}_{\mathrm{3}} {d}\right]/\mathrm{2} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{3}{a}}{\mathrm{2}}×\frac{\sqrt{\mathrm{3}{a}^{\mathrm{2}} +\mathrm{4}{h}^{\mathrm{2}} }}{\mathrm{4}}+{a}×\frac{\mathrm{3}\sqrt{\mathrm{3}{a}^{\mathrm{2}} +\mathrm{4}{h}^{\mathrm{2}} }}{\mathrm{8}}+\frac{{a}}{\mathrm{4}}×\frac{\sqrt{\mathrm{3}{a}^{\mathrm{2}} +\mathrm{4}{h}^{\mathrm{2}} }}{\mathrm{8}}\right] \\ $$$$\Rightarrow\boldsymbol{{A}}=\frac{\mathrm{25}\boldsymbol{{a}}\sqrt{\mathrm{3}\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{4}\boldsymbol{{h}}^{\mathrm{2}} }}{\mathrm{64}} \\ $$
Commented by ajfour last updated on 25/Nov/18
$${excellent}\:{Sir},\:{but}\:{answer}\:{is}\:{bit} \\ $$$${different}.. \\ $$
Commented by mr W last updated on 25/Nov/18
$${I}\:{made}\:{a}\:{little}\:{mistake},\:{now}\:{it}'{s}\:{fixed}. \\ $$
Commented by ajfour last updated on 25/Nov/18

$${Really}\:{Correct}\:{now},\:{and}\:{beyond} \\ $$$${all}\:{admiration}\:{and}\:{praise}\:{Sir};\: \\ $$$$\frac{{b}_{\mathrm{3}} }{{a}}\:=\:\frac{{h}−{f}}{{h}}\:\:\:\left({please}\:{help};\:{how}\:?\right) \\ $$
Commented by mr W last updated on 26/Nov/18
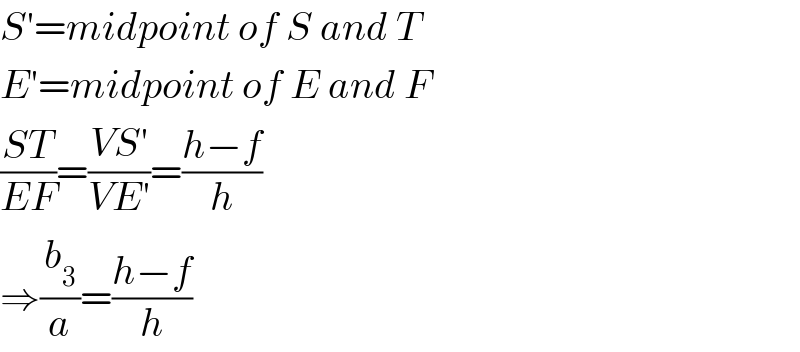
$${S}'={midpoint}\:{of}\:{S}\:{and}\:{T} \\ $$$${E}'={midpoint}\:{of}\:{E}\:{and}\:{F} \\ $$$$\frac{{ST}}{{EF}}=\frac{{VS}'}{{VE}'}=\frac{{h}−{f}}{{h}} \\ $$$$\Rightarrow\frac{{b}_{\mathrm{3}} }{{a}}=\frac{{h}−{f}}{{h}} \\ $$
