
Question Number 48484 by Meritguide1234 last updated on 24/Nov/18
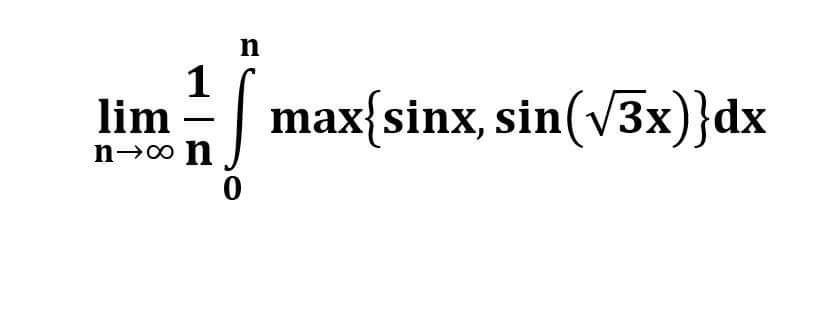
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Nov/18
![trying to solve let in place of (√3) putting a a=(√3) finding the values of x so that sinax=sinx ax=kπ+(−1)^k x ax=π+(−1)^1 x for k=1 x=(π/(a+1)) ax=2π+(−1)^2 x for k=2 x=((2π)/(a−1)) ax=3π+(−1)^3 x for k=3 x=((3π)/(a+1)) ax=4π+(−1)^4 x for k=4 x=((4π)/(a−1)) ax=5π+(−1)^5 x for k=5 x=((5π)/(a+1)) ax=(n−1)π+(−1)^(n−1) x k=n−1 x=(((n−1)π)/(a−(−1)^(n−1) )) ax=nπ+(−1)^n x k=n x=((nπ)/(a−(−1)^n )) now in between two consequtive interval the value of max{sinx,sinax} is=1 ∫_0 ^(π/(a+1)) 1.dx+∫_(π/(a+1)) ^((2π)/(a−1)) dx+∫_((2π)/(a−1 )) ^((3π)/(a+1)) dx+∫_((3π)/(a+1)) ^((4π)/(a−1)) dx+...+ ∫_(((n−1)π)/(a−(−1)^(n−1) )) ^((nπ)/(a−(−1)^n )) dx ={(π/(a+1))−0}+{((2π)/(a−1))−(π/(a+1))}+{((3π)/(a+1))−((2π)/(a−1))}+...+ {((nπ)/(a−(−1)^n ))−(((n−1)π)/(a−(−1)^(n−1) ))} all terms cacelled each other the value of intregal is =((nπ)/(a−(−1)^n ))−(((n−1)π)/(a−(−1)^(n−1) )) now lim_(n→∞) (1/n)[((nπ)/(a−(−1)^n ))−(((n−1)π)/(a−(−1)^(n−1) ))] =lim_(n→∞) (1/n)[n{(π/(a−(−1)^n ))−(π/(a−(−1)^(n−1) ))}+(π/(a−(−1)^(n−1) ))] so ans is =(π/(a+1)) or (π/(a−1)) =(π/((√3) +1)) or (π/((√3) −1)) i have tried to solve... ... ...](Q48490.png)
$${trying}\:{to}\:{solve} \\ $$$${let}\:{in}\:{place}\:{of}\:\sqrt{\mathrm{3}}\:\:{putting}\:\:{a}\:\:\:\:\:{a}=\sqrt{\mathrm{3}}\: \\ $$$${finding}\:{the}\:{values}\:{of}\:{x}\:\:{so}\:{that} \\ $$$${sinax}={sinx} \\ $$$${ax}={k}\pi+\left(−\mathrm{1}\right)^{{k}} {x} \\ $$$${ax}=\pi+\left(−\mathrm{1}\right)^{\mathrm{1}} {x}\:\:{for}\:{k}=\mathrm{1}\:\:\:{x}=\frac{\pi}{{a}+\mathrm{1}} \\ $$$${ax}=\mathrm{2}\pi+\left(−\mathrm{1}\right)^{\mathrm{2}} {x}\:\:\:\:\:\:\:\:\:{for}\:{k}=\mathrm{2}\:\:\:{x}=\frac{\mathrm{2}\pi}{{a}−\mathrm{1}} \\ $$$${ax}=\mathrm{3}\pi+\left(−\mathrm{1}\right)^{\mathrm{3}} {x}\:\:\:{for}\:{k}=\mathrm{3}\:\:{x}=\frac{\mathrm{3}\pi}{{a}+\mathrm{1}} \\ $$$${ax}=\mathrm{4}\pi+\left(−\mathrm{1}\right)^{\mathrm{4}} {x}\:\:{for}\:{k}=\mathrm{4}\:\:\:{x}=\frac{\mathrm{4}\pi}{{a}−\mathrm{1}} \\ $$$${ax}=\mathrm{5}\pi+\left(−\mathrm{1}\right)^{\mathrm{5}} {x}\:\:\:{for}\:{k}=\mathrm{5}\:\:\:\:{x}=\frac{\mathrm{5}\pi}{{a}+\mathrm{1}} \\ $$$${ax}=\left({n}−\mathrm{1}\right)\pi+\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {x}\:\:\:{k}={n}−\mathrm{1}\:\:{x}=\frac{\left({n}−\mathrm{1}\right)\pi}{{a}−\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} } \\ $$$${ax}={n}\pi+\left(−\mathrm{1}\right)^{{n}} {x}\:\:{k}={n}\:\:\:{x}=\frac{{n}\pi}{{a}−\left(−\mathrm{1}\right)^{{n}} } \\ $$$${now}\:\:{in}\:{between}\:{two}\:{consequtive}\:{interval}\:{the}\:{value}\:{of} \\ $$$${max}\left\{{sinx},{sinax}\right\}\:{is}=\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{{a}+\mathrm{1}}} \mathrm{1}.{dx}+\int_{\frac{\pi}{{a}+\mathrm{1}}} ^{\frac{\mathrm{2}\pi}{{a}−\mathrm{1}}} \:{dx}+\int_{\frac{\mathrm{2}\pi}{{a}−\mathrm{1}\:}} ^{\frac{\mathrm{3}\pi}{{a}+\mathrm{1}}} \:{dx}+\int_{\frac{\mathrm{3}\pi}{{a}+\mathrm{1}}} ^{\frac{\mathrm{4}\pi}{{a}−\mathrm{1}}} \:{dx}+...+ \\ $$$$\:\:\int_{\frac{\left({n}−\mathrm{1}\right)\pi}{{a}−\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }} ^{\frac{{n}\pi}{{a}−\left(−\mathrm{1}\right)^{{n}} }} \:{dx} \\ $$$$=\left\{\frac{\pi}{{a}+\mathrm{1}}−\mathrm{0}\right\}+\left\{\frac{\mathrm{2}\pi}{{a}−\mathrm{1}}−\frac{\pi}{{a}+\mathrm{1}}\right\}+\left\{\frac{\mathrm{3}\pi}{{a}+\mathrm{1}}−\frac{\mathrm{2}\pi}{{a}−\mathrm{1}}\right\}+...+ \\ $$$$\left\{\frac{{n}\pi}{{a}−\left(−\mathrm{1}\right)^{{n}} }−\frac{\left({n}−\mathrm{1}\right)\pi}{{a}−\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }\right\} \\ $$$$\:{all}\:{terms}\:{cacelled}\:{each}\:{other}\: \\ $$$${the}\:{value}\:{of}\:{intregal}\:{is} \\ $$$$=\frac{{n}\pi}{{a}−\left(−\mathrm{1}\right)^{{n}} }−\frac{\left({n}−\mathrm{1}\right)\pi}{{a}−\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} } \\ $$$${now}\: \\ $$$${li}\underset{{n}\rightarrow\infty} {{m}}\:\frac{\mathrm{1}}{{n}}\left[\frac{{n}\pi}{{a}−\left(−\mathrm{1}\right)^{{n}} }−\frac{\left({n}−\mathrm{1}\right)\pi}{{a}−\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }\right] \\ $$$$={li}\underset{{n}\rightarrow\infty} {{m}}\:\frac{\mathrm{1}}{{n}}\left[{n}\left\{\frac{\pi}{{a}−\left(−\mathrm{1}\right)^{{n}} }−\frac{\pi}{{a}−\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }\right\}+\frac{\pi}{{a}−\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }\right] \\ $$$${so}\:{ans}\:{is}\:=\frac{\pi}{{a}+\mathrm{1}}\:{or}\:\frac{\pi}{{a}−\mathrm{1}} \\ $$$$=\frac{\pi}{\sqrt{\mathrm{3}}\:+\mathrm{1}}\:\:{or}\:\frac{\pi}{\sqrt{\mathrm{3}}\:−\mathrm{1}} \\ $$$${i}\:{have}\:{tried}\:{to}\:{solve}... \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$... \\ $$$$... \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
