
Question Number 48388 by Tawa1 last updated on 23/Nov/18
Commented by Tawa1 last updated on 23/Nov/18

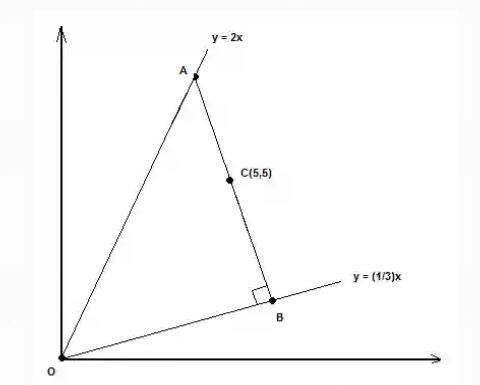
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{Area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle} \\ $$
Answered by mr W last updated on 23/Nov/18
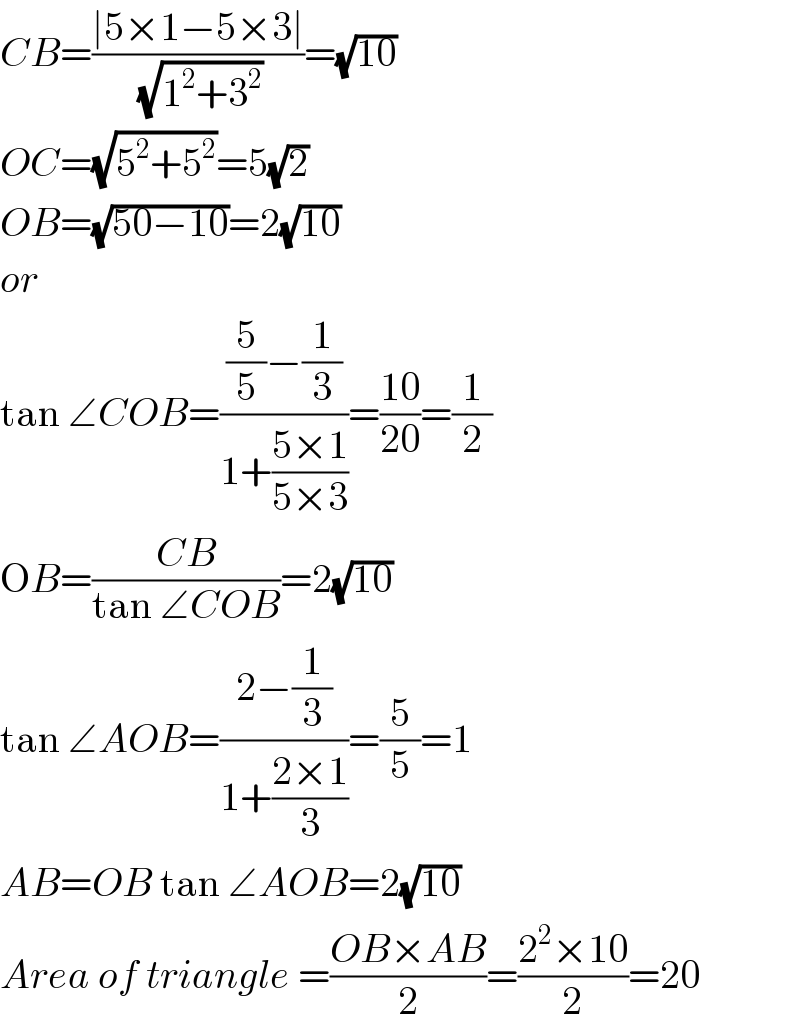
$${CB}=\frac{\mid\mathrm{5}×\mathrm{1}−\mathrm{5}×\mathrm{3}\mid}{\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }}=\sqrt{\mathrm{10}} \\ $$$${OC}=\sqrt{\mathrm{5}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} }=\mathrm{5}\sqrt{\mathrm{2}} \\ $$$${OB}=\sqrt{\mathrm{50}−\mathrm{10}}=\mathrm{2}\sqrt{\mathrm{10}} \\ $$$${or} \\ $$$$\mathrm{tan}\:\angle{COB}=\frac{\frac{\mathrm{5}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{1}+\frac{\mathrm{5}×\mathrm{1}}{\mathrm{5}×\mathrm{3}}}=\frac{\mathrm{10}}{\mathrm{20}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{O}{B}=\frac{{CB}}{\mathrm{tan}\:\angle{COB}}=\mathrm{2}\sqrt{\mathrm{10}} \\ $$$$\mathrm{tan}\:\angle{AOB}=\frac{\mathrm{2}−\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{1}+\frac{\mathrm{2}×\mathrm{1}}{\mathrm{3}}}=\frac{\mathrm{5}}{\mathrm{5}}=\mathrm{1} \\ $$$${AB}={OB}\:\mathrm{tan}\:\angle{AOB}=\mathrm{2}\sqrt{\mathrm{10}} \\ $$$${Area}\:{of}\:{triangle}\:=\frac{{OB}×{AB}}{\mathrm{2}}=\frac{\mathrm{2}^{\mathrm{2}} ×\mathrm{10}}{\mathrm{2}}=\mathrm{20} \\ $$
Commented by Tawa1 last updated on 24/Nov/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 23/Nov/18
![eqn AB (y−5)=−3(x−5) y−5+3x−15=0 y+3x=20 point A intersection between y+3x=20 andy=2x 2x+3x=20 x=4 so y=8 A(4,8) B is the intersectiin between y=(x/3) and y+3x=20 (x/3)+3x=20 x=6 y=2 so A(4,8) B(6,2) O(0,0) area of OAB (1/2)[x_1 (y_2 −y_3 )+x_2 (y_3 −y_1 )+x_3 (y_1 −y_2 )] =(1/2)[4(2−0)+6(0−8)+0(8−2)] =(1/2)[−40] so area is 20 unit...](Q48391.png)
$${eqn}\:{AB}\:\left({y}−\mathrm{5}\right)=−\mathrm{3}\left({x}−\mathrm{5}\right) \\ $$$${y}−\mathrm{5}+\mathrm{3}{x}−\mathrm{15}=\mathrm{0} \\ $$$${y}+\mathrm{3}{x}=\mathrm{20} \\ $$$${point}\:\:{A}\:{intersection}\:{between}\:{y}+\mathrm{3}{x}=\mathrm{20}\:{andy}=\mathrm{2}{x} \\ $$$$\mathrm{2}{x}+\mathrm{3}{x}=\mathrm{20}\:\:\:{x}=\mathrm{4}\:\:\:{so}\:{y}=\mathrm{8}\:\:{A}\left(\mathrm{4},\mathrm{8}\right) \\ $$$${B}\:{is}\:{the}\:{intersectiin}\:{between}\:{y}=\frac{{x}}{\mathrm{3}}\:\:{and}\:{y}+\mathrm{3}{x}=\mathrm{20} \\ $$$$\frac{{x}}{\mathrm{3}}+\mathrm{3}{x}=\mathrm{20}\:\:\:{x}=\mathrm{6}\:\:{y}=\mathrm{2} \\ $$$${so}\:{A}\left(\mathrm{4},\mathrm{8}\right)\:\:{B}\left(\mathrm{6},\mathrm{2}\right)\:\:\:{O}\left(\mathrm{0},\mathrm{0}\right) \\ $$$${area}\:{of}\:{OAB} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left[{x}_{\mathrm{1}} \left({y}_{\mathrm{2}} −{y}_{\mathrm{3}} \right)+{x}_{\mathrm{2}} \left({y}_{\mathrm{3}} −{y}_{\mathrm{1}} \right)+{x}_{\mathrm{3}} \left({y}_{\mathrm{1}} −{y}_{\mathrm{2}} \right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{4}\left(\mathrm{2}−\mathrm{0}\right)+\mathrm{6}\left(\mathrm{0}−\mathrm{8}\right)+\mathrm{0}\left(\mathrm{8}−\mathrm{2}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[−\mathrm{40}\right] \\ $$$${so}\:{area}\:{is}\:\mathrm{20}\:{unit}... \\ $$
Commented by Tawa1 last updated on 24/Nov/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
