Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 48368 by behi83417@gmail.com last updated on 22/Nov/18

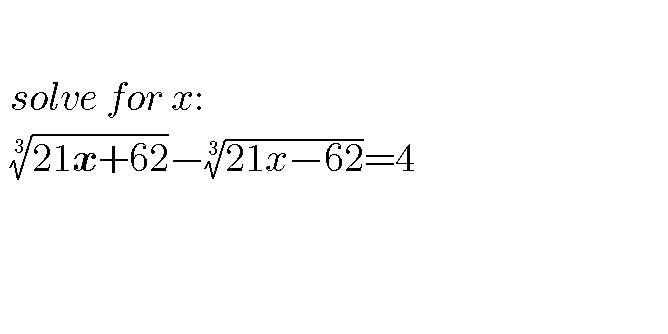
Answered by MJS last updated on 22/Nov/18

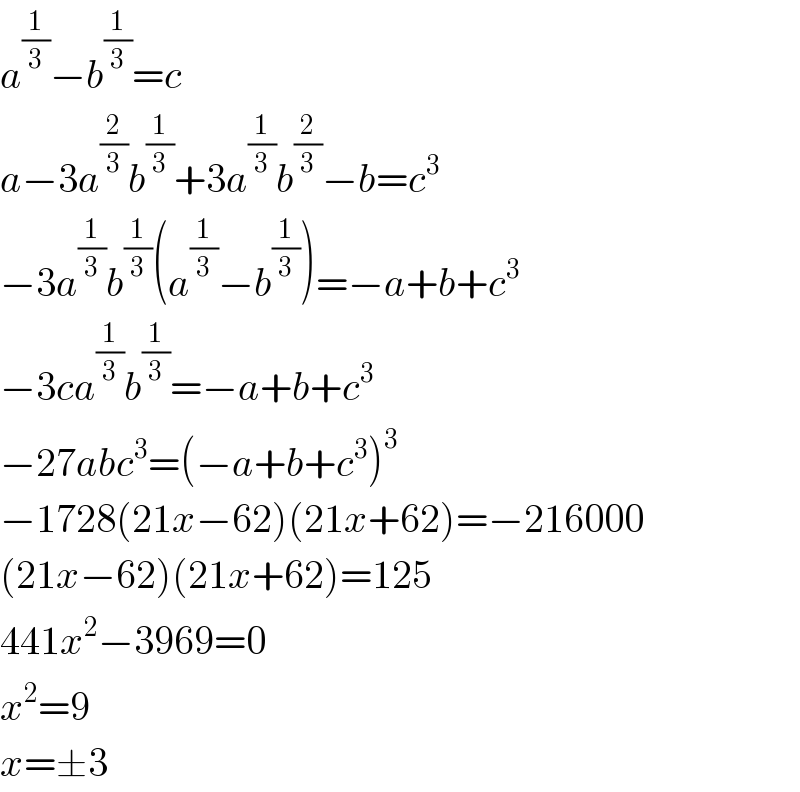
a^(1/3) −b^(1/3) =c a−3a^(2/3) b^(1/3) +3a^(1/3) b^(2/3) −b=c^3 −3a^(1/3) b^(1/3) (a^(1/3) −b^(1/3) )=−a+b+c^3 −3ca^(1/3) b^(1/3) =−a+b+c^3 −27abc^3 =(−a+b+c^3 )^3 −1728(21x−62)(21x+62)=−216000 (21x−62)(21x+62)=125 441x^2 −3969=0 x^2 =9 x=±3

$${a}^{\frac{\mathrm{1}}{\mathrm{3}}} −{b}^{\frac{\mathrm{1}}{\mathrm{3}}} ={c} \\ $$$${a}−\mathrm{3}{a}^{\frac{\mathrm{2}}{\mathrm{3}}} {b}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{3}{a}^{\frac{\mathrm{1}}{\mathrm{3}}} {b}^{\frac{\mathrm{2}}{\mathrm{3}}} −{b}={c}^{\mathrm{3}} \\ $$$$−\mathrm{3}{a}^{\frac{\mathrm{1}}{\mathrm{3}}} {b}^{\frac{\mathrm{1}}{\mathrm{3}}} \left({a}^{\frac{\mathrm{1}}{\mathrm{3}}} −{b}^{\frac{\mathrm{1}}{\mathrm{3}}} \right)=−{a}+{b}+{c}^{\mathrm{3}} \\ $$$$−\mathrm{3}{ca}^{\frac{\mathrm{1}}{\mathrm{3}}} {b}^{\frac{\mathrm{1}}{\mathrm{3}}} =−{a}+{b}+{c}^{\mathrm{3}} \\ $$$$−\mathrm{27}{abc}^{\mathrm{3}} =\left(−{a}+{b}+{c}^{\mathrm{3}} \right)^{\mathrm{3}} \\ $$$$−\mathrm{1728}\left(\mathrm{21}{x}−\mathrm{62}\right)\left(\mathrm{21}{x}+\mathrm{62}\right)=−\mathrm{216000} \\ $$$$\left(\mathrm{21}{x}−\mathrm{62}\right)\left(\mathrm{21}{x}+\mathrm{62}\right)=\mathrm{125} \\ $$$$\mathrm{441}{x}^{\mathrm{2}} −\mathrm{3969}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} =\mathrm{9} \\ $$$${x}=\pm\mathrm{3} \\ $$

Commented by behi83417@gmail.com last updated on 23/Nov/18

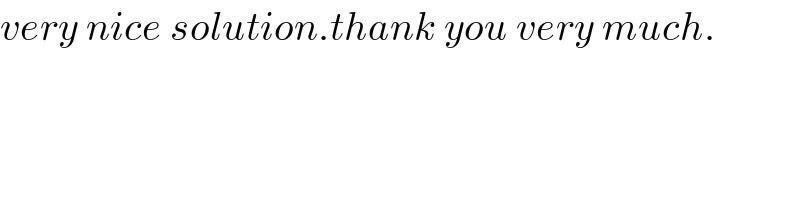
very nice solution.thank you very much.

$${very}\:{nice}\:{solution}.{thank}\:{you}\:{very}\:{much}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com