
Question Number 48359 by ajfour last updated on 22/Nov/18

Answered by mr W last updated on 23/Nov/18
![(x^2 /a^2 )+(y^2 /b^2 )=1 (x/a^2 )+((yy′)/b^2 )=0⇒y′=−((b^2 x)/(a^2 y)) (x−r)^2 +(y−r)^2 =r^2 (x−r)+(y−r)y′=0⇒y′=−((x−r)/(y−r)) T(h,k) (h^2 /a^2 )+(k^2 /b^2 )=1 (h−r)^2 +(k−r)^2 =r^2 ((b^2 h)/(a^2 k))=(h/(b+k))=(r/(b+r)) ⇒b^2 (b+k)=a^2 k⇒k=(b^3 /(a^2 −b^2 )) (h^2 /a^2 )=1−(b^6 /(b^2 (a^2 −b^2 )^2 ))=1−((b^2 /(a^2 −b^2 )))^2 =((a^2 (a^2 −2b^2 ))/((a^2 −b^2 ))) ⇒h=((a^2 (√(a^2 −2b^2 )))/(a^2 −b^2 )) (b+k−h)r=bh ⇒r=((bh)/(b+k−h))=((ba^2 (√(a^2 −2b^2 )))/((a^2 −b^2 )(b+(b^3 /(a^2 −b^2 ))−((a^2 (√(a^2 −2b^2 )))/(a^2 −b^2 )))))=((b(√(a^2 −2b^2 )))/(b−(√(a^2 −2b^2 )))) with λ=(a/b) ⇒k=(b/(λ^2 −1)) ⇒h=((bλ^2 (√(λ^2 −2)))/(λ^2 −1)) ⇒r=((b(√(λ^2 −2)))/(1−(√(λ^2 −2)))) ⇒(h/r)=((λ^2 (1−(√(λ^2 −2))))/(λ^2 −1)) ⇒(k/r)=((1−(√(λ^2 −2)))/((λ^2 −1)(√(λ^2 −2)))) ((h/r)−1)^2 +((k/r)−1)^2 =1 [((λ^2 (1−(√(λ^2 −2))))/(λ^2 −1))−1]^2 +[((1−(√(λ^2 −2)))/((λ^2 −1)(√(λ^2 −2))))−1]^2 =1 [((1−λ^2 (√(λ^2 −2)))/(λ^2 −1))]^2 +[((1−λ^2 (√(λ^2 −2)))/((λ^2 −1)(√(λ^2 −2))))]^2 =1 ((1−λ^2 (√(λ^2 −2)))/(√((λ^2 −1)(λ^2 −2))))=1 ⇒(λ^2 +(√(λ^2 −1)))(√(λ^2 −2))=1 ⇒λ=(a/b)≈1.4494](Q48383.png)
$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{{x}}{{a}^{\mathrm{2}} }+\frac{{yy}'}{{b}^{\mathrm{2}} }=\mathrm{0}\Rightarrow{y}'=−\frac{{b}^{\mathrm{2}} {x}}{{a}^{\mathrm{2}} {y}} \\ $$$$\left({x}−{r}\right)^{\mathrm{2}} +\left({y}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left({x}−{r}\right)+\left({y}−{r}\right){y}'=\mathrm{0}\Rightarrow{y}'=−\frac{{x}−{r}}{{y}−{r}} \\ $$$${T}\left({h},{k}\right) \\ $$$$\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{k}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\left({h}−{r}\right)^{\mathrm{2}} +\left({k}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\frac{{b}^{\mathrm{2}} {h}}{{a}^{\mathrm{2}} {k}}=\frac{{h}}{{b}+{k}}=\frac{{r}}{{b}+{r}} \\ $$$$\Rightarrow{b}^{\mathrm{2}} \left({b}+{k}\right)={a}^{\mathrm{2}} {k}\Rightarrow{k}=\frac{{b}^{\mathrm{3}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$$\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} }=\mathrm{1}−\frac{{b}^{\mathrm{6}} }{{b}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} }=\mathrm{1}−\left(\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} \left({a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} \right)}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow{h}=\frac{{a}^{\mathrm{2}} \sqrt{{a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} }}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$$\left({b}+{k}−{h}\right){r}={bh} \\ $$$$\Rightarrow{r}=\frac{{bh}}{{b}+{k}−{h}}=\frac{{ba}^{\mathrm{2}} \sqrt{{a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} }}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({b}+\frac{{b}^{\mathrm{3}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }−\frac{{a}^{\mathrm{2}} \sqrt{{a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} }}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)}=\frac{{b}\sqrt{{a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} }}{{b}−\sqrt{{a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} }} \\ $$$${with}\:\lambda=\frac{{a}}{{b}} \\ $$$$\Rightarrow{k}=\frac{{b}}{\lambda^{\mathrm{2}} −\mathrm{1}} \\ $$$$\Rightarrow{h}=\frac{{b}\lambda^{\mathrm{2}} \sqrt{\lambda^{\mathrm{2}} −\mathrm{2}}}{\lambda^{\mathrm{2}} −\mathrm{1}} \\ $$$$\Rightarrow{r}=\frac{{b}\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}}}{\mathrm{1}−\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}}} \\ $$$$\Rightarrow\frac{{h}}{{r}}=\frac{\lambda^{\mathrm{2}} \left(\mathrm{1}−\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}}\right)}{\lambda^{\mathrm{2}} −\mathrm{1}} \\ $$$$\Rightarrow\frac{{k}}{{r}}=\frac{\mathrm{1}−\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}}}{\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}}} \\ $$$$\left(\frac{{h}}{{r}}−\mathrm{1}\right)^{\mathrm{2}} +\left(\frac{{k}}{{r}}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\left[\frac{\lambda^{\mathrm{2}} \left(\mathrm{1}−\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}}\right)}{\lambda^{\mathrm{2}} −\mathrm{1}}−\mathrm{1}\right]^{\mathrm{2}} +\left[\frac{\mathrm{1}−\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}}}{\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}}}−\mathrm{1}\right]^{\mathrm{2}} =\mathrm{1} \\ $$$$\left[\frac{\mathrm{1}−\lambda^{\mathrm{2}} \sqrt{\lambda^{\mathrm{2}} −\mathrm{2}}}{\lambda^{\mathrm{2}} −\mathrm{1}}\right]^{\mathrm{2}} +\left[\frac{\mathrm{1}−\lambda^{\mathrm{2}} \sqrt{\lambda^{\mathrm{2}} −\mathrm{2}}}{\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}}}\right]^{\mathrm{2}} =\mathrm{1} \\ $$$$\frac{\mathrm{1}−\lambda^{\mathrm{2}} \sqrt{\lambda^{\mathrm{2}} −\mathrm{2}}}{\sqrt{\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)\left(\lambda^{\mathrm{2}} −\mathrm{2}\right)}}=\mathrm{1} \\ $$$$\Rightarrow\left(\lambda^{\mathrm{2}} +\sqrt{\lambda^{\mathrm{2}} −\mathrm{1}}\right)\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}}=\mathrm{1} \\ $$$$\Rightarrow\lambda=\frac{{a}}{{b}}\approx\mathrm{1}.\mathrm{4494} \\ $$
Commented by ajfour last updated on 23/Nov/18

$${Great}!\: \\ $$
Commented by mr W last updated on 23/Nov/18
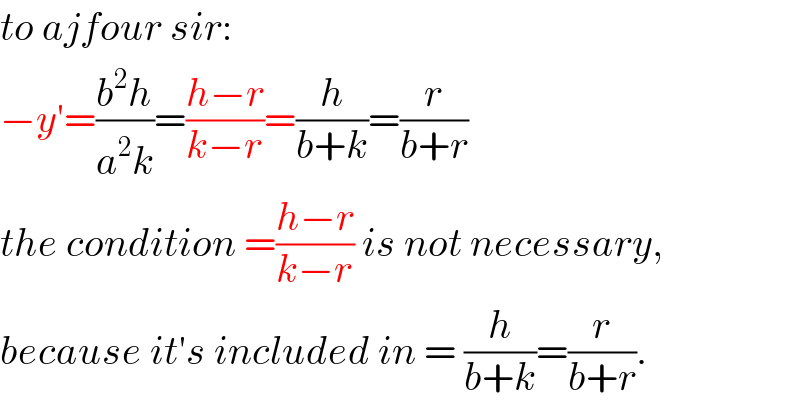
$${to}\:{ajfour}\:{sir}: \\ $$$$−{y}'=\frac{{b}^{\mathrm{2}} {h}}{{a}^{\mathrm{2}} {k}}=\frac{{h}−{r}}{{k}−{r}}=\frac{{h}}{{b}+{k}}=\frac{{r}}{{b}+{r}} \\ $$$${the}\:{condition}\:=\frac{{h}−{r}}{{k}−{r}}\:{is}\:{not}\:{necessary}, \\ $$$${because}\:{it}'{s}\:{included}\:{in}\:=\:\frac{{h}}{{b}+{k}}=\frac{{r}}{{b}+{r}}. \\ $$
Commented by ajfour last updated on 23/Nov/18
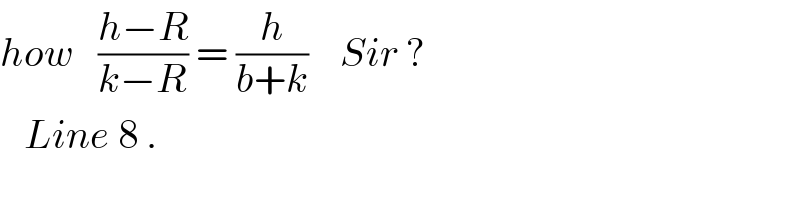
$${how}\:\:\:\frac{{h}−{R}}{{k}−{R}}\:=\:\frac{{h}}{{b}+{k}}\:\:\:\:{Sir}\:? \\ $$$$\:\:\:{Line}\:\mathrm{8}\:. \\ $$
Commented by MJS last updated on 23/Nov/18

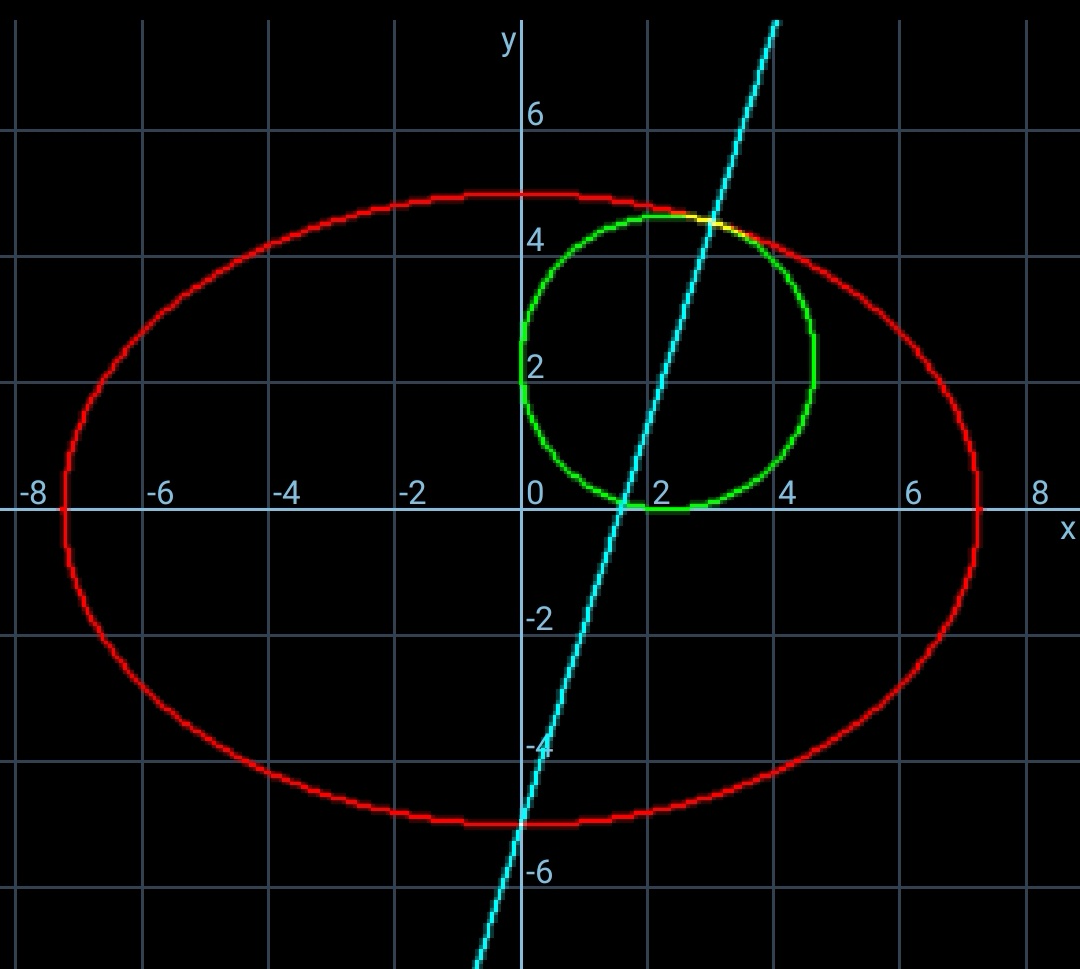
$$\mathrm{you}'\mathrm{re}\:\mathrm{losing}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{solution}\:\mathrm{by}\:\mathrm{taking}\:\mathrm{the} \\ $$$$\mathrm{root}\:\mathrm{in}\:\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{line}\:\mathrm{from}\:\mathrm{the}\:\mathrm{bottom}. \\ $$$$\lambda=\pm\mathrm{1}.\mathrm{44941}\:\vee\:\lambda=\pm\mathrm{1}.\mathrm{60446} \\ $$$$\Rightarrow\:\mathrm{2}\:\mathrm{circles}\:\mathrm{are}\:\mathrm{possible} \\ $$
Commented by mr W last updated on 23/Nov/18
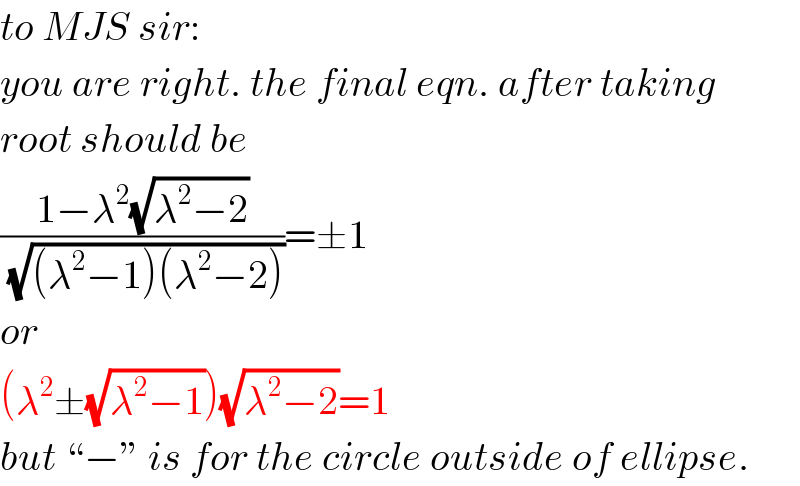
$${to}\:{MJS}\:{sir}: \\ $$$${you}\:{are}\:{right}.\:{the}\:{final}\:{eqn}.\:{after}\:{taking} \\ $$$${root}\:{should}\:{be}\: \\ $$$$\frac{\mathrm{1}−\lambda^{\mathrm{2}} \sqrt{\lambda^{\mathrm{2}} −\mathrm{2}}}{\sqrt{\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)\left(\lambda^{\mathrm{2}} −\mathrm{2}\right)}}=\pm\mathrm{1} \\ $$$${or} \\ $$$$\left(\lambda^{\mathrm{2}} \pm\sqrt{\lambda^{\mathrm{2}} −\mathrm{1}}\right)\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}}=\mathrm{1} \\ $$$${but}\:``−''\:{is}\:{for}\:{the}\:{circle}\:{outside}\:{of}\:{ellipse}. \\ $$
Commented by mr W last updated on 23/Nov/18

Commented by mr W last updated on 23/Nov/18
Commented by ajfour last updated on 23/Nov/18
$${Thank}\:{you}\:{both}.\:{I}\:{should}\:{have} \\ $$$${drawn}\:{two}\:{such}\:{circles}\:{in}\:{the} \\ $$$${question}\:{diagram}\:{itself}.. \\ $$
Answered by MJS last updated on 22/Nov/18
![T= ((((a^2 (√(a^2 −2b^2 )))/(a^2 −b^2 ))),((b^3 /(a^2 −b^2 ))) ) B= ((0),((−b)) ) from C∈y=x ∧ C∈BT ⇒ ⇒ C= ((r),(r) ) r=((b(√(a^2 −2b^2 )))/(b−(√(a^2 −2b^2 )))) I put a=1 ∣CT∣^2 =r^2 this leads to a 6^(th) degree polynome which had 2 real solutions: a=1; b_1 =.689937; c_1 =1.95025 [circle touches ellipse from outside] a=1; b_2 =.623263; c_2 =.320906 [circle touches ellipse from inside]](Q48375.png)
$${T}=\begin{pmatrix}{\frac{{a}^{\mathrm{2}} \sqrt{{a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} }}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}\\{\frac{{b}^{\mathrm{3}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}\end{pmatrix}\:\:{B}=\begin{pmatrix}{\mathrm{0}}\\{−{b}}\end{pmatrix} \\ $$$$\mathrm{from}\:{C}\in{y}={x}\:\wedge\:{C}\in{BT}\:\Rightarrow \\ $$$$\Rightarrow\:{C}=\begin{pmatrix}{{r}}\\{{r}}\end{pmatrix}\:\:{r}=\frac{{b}\sqrt{{a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} }}{{b}−\sqrt{{a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} }} \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{put}\:{a}=\mathrm{1} \\ $$$$\mid{CT}\mid^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\mathrm{this}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{a}\:\mathrm{6}^{\mathrm{th}} \:\mathrm{degree}\:\mathrm{polynome}\:\mathrm{which}\:\mathrm{had} \\ $$$$\mathrm{2}\:\mathrm{real}\:\mathrm{solutions}: \\ $$$${a}=\mathrm{1};\:{b}_{\mathrm{1}} =.\mathrm{689937};\:{c}_{\mathrm{1}} =\mathrm{1}.\mathrm{95025} \\ $$$$\:\:\:\:\:\left[\mathrm{circle}\:\mathrm{touches}\:\mathrm{ellipse}\:\mathrm{from}\:\mathrm{outside}\right] \\ $$$${a}=\mathrm{1};\:{b}_{\mathrm{2}} =.\mathrm{623263};\:{c}_{\mathrm{2}} =.\mathrm{320906} \\ $$$$\:\:\:\:\:\left[\mathrm{circle}\:\mathrm{touches}\:\mathrm{ellipse}\:\mathrm{from}\:\mathrm{inside}\right] \\ $$
Commented by ajfour last updated on 23/Nov/18
$${Sir},\:{first}\:{of}\:{all}\:{how}\:{to}\:{arrive}\:{at} \\ $$$${coordinates}\:{of}\:{T}\:\:;\:{your}\:{method}\:? \\ $$
Commented by MJS last updated on 23/Nov/18

$${y}=\frac{{b}}{{a}}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$$\mathrm{normal}\:\mathrm{in}\:{x}={t}:\:{y}={kx}+{d} \\ $$$${y}'=−\frac{{bt}}{{a}\sqrt{{a}^{\mathrm{2}} −{t}^{\mathrm{2}} }}\:\Rightarrow\:\:{k}=\frac{{a}\sqrt{{a}^{\mathrm{2}} −{t}^{\mathrm{2}} }}{{bt}} \\ $$$${d}={y}−{kt}=−\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{ab}}\sqrt{{a}^{\mathrm{2}} −{t}^{\mathrm{2}} } \\ $$$$\mathrm{but}\:{d}=−{b}\:\Rightarrow\:{t}=\pm\frac{{a}^{\mathrm{2}} \sqrt{{a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{3}} }}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:\wedge\:{a}>{b}\:\wedge\:{a}^{\mathrm{2}} \geqslant\mathrm{2}{b}^{\mathrm{2}} \\ $$$${u}=\frac{{b}}{{a}}\sqrt{{a}^{\mathrm{2}} −{t}^{\mathrm{2}} }=\frac{{b}^{\mathrm{3}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$$\mathrm{line}\:{BT}:\:{y}=\frac{{b}+{u}}{{t}}{x}−{b} \\ $$$$\left({y}=\frac{{b}+{u}}{{t}}{x}−{b}\right)\cap\left({y}={x}\right)\:\Rightarrow\:{x}=\frac{{bt}}{{b}−{t}+{u}}=\frac{{b}\sqrt{{a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} }}{{b}−\sqrt{{a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} }}={r} \\ $$$$\mid{CT}\mid^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\mathrm{this}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{3}} \sqrt{{a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} }=\left({a}−{b}\right)^{\mathrm{3}} \left({a}+{b}\right)^{\mathrm{3}} \\ $$$$\mathrm{squaring}\:\mathrm{leads}\:\mathrm{to} \\ $$$${a}^{\mathrm{12}} −\mathrm{6}{a}^{\mathrm{10}} {b}^{\mathrm{2}} +\mathrm{15}{a}^{\mathrm{8}} {b}^{\mathrm{4}} −\mathrm{24}{a}^{\mathrm{6}} {b}^{\mathrm{6}} +\mathrm{23}{a}^{\mathrm{4}} {b}^{\mathrm{8}} −\mathrm{6}{a}^{\mathrm{2}} {b}^{\mathrm{10}} +{b}^{\mathrm{12}} =\mathrm{0} \\ $$$${a}=\sqrt{{p}};\:{b}=\sqrt{{q}} \\ $$$${p}^{\mathrm{6}} −\mathrm{6}{p}^{\mathrm{5}} {q}+\mathrm{15}{p}^{\mathrm{4}} {q}^{\mathrm{2}} −\mathrm{24}{p}^{\mathrm{3}} {q}^{\mathrm{3}} +\mathrm{23}{p}^{\mathrm{2}} {q}^{\mathrm{4}} −\mathrm{6}{pq}^{\mathrm{5}} +{q}^{\mathrm{6}} =\mathrm{0} \\ $$$${p}=\mathrm{1} \\ $$$${q}^{\mathrm{6}} −\mathrm{6}{q}^{\mathrm{5}} +\mathrm{23}{q}^{\mathrm{4}} −\mathrm{24}{q}^{\mathrm{3}} +\mathrm{15}{q}^{\mathrm{2}} −\mathrm{6}{q}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{approximating}\:\Rightarrow\:{q}=.\mathrm{388457}\:\vee\:{q}=.\mathrm{476013} \\ $$$$\Rightarrow\:{b}=.\mathrm{623263}\:\vee\:{b}=.\mathrm{689937} \\ $$
