
Question Number 48285 by ajfour last updated on 21/Nov/18
Commented by ajfour last updated on 21/Nov/18
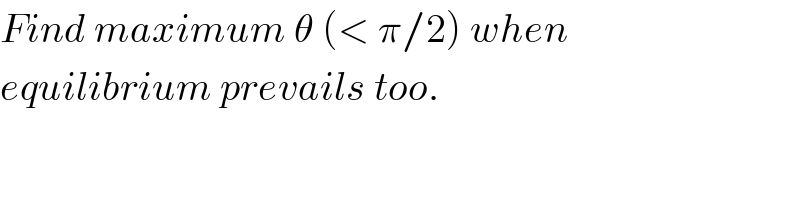
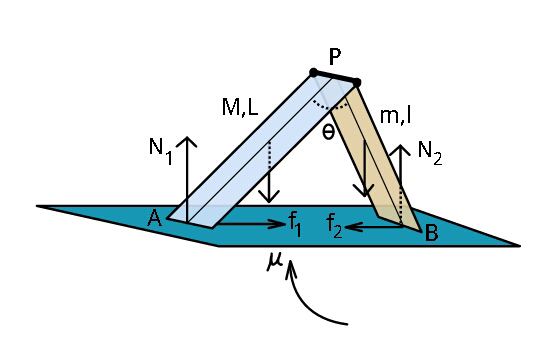
$${Find}\:{maximum}\:\theta\:\left(<\:\pi/\mathrm{2}\right)\:{when} \\ $$$${equilibrium}\:{prevails}\:{too}. \\ $$
Commented by ajfour last updated on 22/Nov/18
Answered by mr W last updated on 23/Nov/18
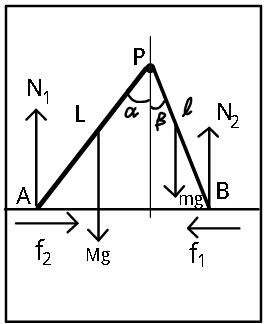
![α=inclination of rod L w.r.t. ground β=inclination of rod l λ=l/L, ϱ=m/M L sin α=l sin β ⇒sin β=((sin α)/λ) cos β=(√(1−((sin^2 α)/λ^2 )))=((√(λ^2 −sin^2 α))/λ) N_1 (L cos α+l cos β)=Mg(((L cos α)/2)+l cos β)+mg((l cos β)/2) ⇒N_1 =((MgL cos α+(2M+m)gl cos β)/(2(L cos α+l cos β))) ⇒N_2 =(((M+2m)gL cos α+mgl cos β)/(2(L cos α+l cos β))) N_1 Lcos α−Mg((L cos α)/2)−f_1 L sin α=0 f_1 =((2N_1 cos α−Mg cos α)/(2 sin α))=μN_1 ⇒ no slipping at point A 2N_1 (cos α−μ sin α)=Mg cos α ((MgL cos α+(2M+m)gl cos β)/((L cos α+l cos β)))(cos α−μ sin α)=Mg cos α ((1+λ(2+ϱ)((cos β)/(cos α)))/((1+λ((cos β)/(cos ϑ)))))(1−μ tan α)=1 ⇒(1−μ tan α)[1+(2+ϱ)((√(λ^2 −sin^2 α))/(cos α))]=1+((√(λ^2 −sin^2 α))/(cos α)) ...(i) ⇒α=α_1 =... similarly N_2 l cos β−mg((l cos β)/2)−f_2 l sin β=0 f_2 =((2N_2 cos β−mg cos β)/(2 sin β))=μN_2 ⇒no slipping at point B 2N_2 (cos β−μ sin β)=mg cos β (((M+2m)gL cos α+mgl cos β)/((L cos α+l cos β)))(cos β−μ sin β)=mg cos β (((1+2ϱ)((cos α)/(cos β))+ϱλ)/((((cos α)/(cos β))+λ)))(1−μ tan β)=ϱ ⇒(((1+2ϱ)cos α+ϱ(√(λ^2 −sin^2 α)))/(cos α+(√(λ^2 −sin^2 α))))(1−((μ sin α)/(√(λ^2 −sin^2 α))))=ϱ ...(ii) ⇒α=α_2 =... ⇒α=max(α_1 ,α_2 ) ⇒β=sin^(−1) (sin α/λ) ⇒θ=π−α−β Example: λ=l/L=0.75, ϱ=m/M=1.5, μ=0.5 α_1 =41.5624° from (i) α_2 =32.2635° from (ii) ⇒α=41.5624° ⇒β=sin^(−1) (sin α/λ)=62.20° ⇒θ_(max) =180−41.56−62.20=76.24°](Q48296.png)
$$\alpha={inclination}\:{of}\:{rod}\:{L}\:{w}.{r}.{t}.\:{ground} \\ $$$$\beta={inclination}\:{of}\:{rod}\:{l} \\ $$$$\lambda={l}/{L},\:\varrho={m}/{M} \\ $$$${L}\:\mathrm{sin}\:\alpha={l}\:\mathrm{sin}\:\beta \\ $$$$\Rightarrow\mathrm{sin}\:\beta=\frac{\mathrm{sin}\:\alpha}{\lambda} \\ $$$$\mathrm{cos}\:\beta=\sqrt{\mathrm{1}−\frac{\mathrm{sin}^{\mathrm{2}} \:\alpha}{\lambda^{\mathrm{2}} }}=\frac{\sqrt{\lambda^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\alpha}}{\lambda} \\ $$$${N}_{\mathrm{1}} \left({L}\:\mathrm{cos}\:\alpha+{l}\:\mathrm{cos}\:\beta\right)={Mg}\left(\frac{{L}\:\mathrm{cos}\:\alpha}{\mathrm{2}}+{l}\:\mathrm{cos}\:\beta\right)+{mg}\frac{{l}\:\mathrm{cos}\:\beta}{\mathrm{2}} \\ $$$$\Rightarrow{N}_{\mathrm{1}} =\frac{{MgL}\:\mathrm{cos}\:\alpha+\left(\mathrm{2}{M}+{m}\right){gl}\:\mathrm{cos}\:\beta}{\mathrm{2}\left({L}\:\mathrm{cos}\:\alpha+{l}\:\mathrm{cos}\:\beta\right)} \\ $$$$\Rightarrow{N}_{\mathrm{2}} =\frac{\left({M}+\mathrm{2}{m}\right){gL}\:\mathrm{cos}\:\alpha+{mgl}\:\mathrm{cos}\:\beta}{\mathrm{2}\left({L}\:\mathrm{cos}\:\alpha+{l}\:\mathrm{cos}\:\beta\right)} \\ $$$$ \\ $$$${N}_{\mathrm{1}} {L}\mathrm{cos}\:\alpha−{Mg}\frac{{L}\:\mathrm{cos}\:\alpha}{\mathrm{2}}−{f}_{\mathrm{1}} {L}\:\mathrm{sin}\:\alpha=\mathrm{0} \\ $$$${f}_{\mathrm{1}} =\frac{\mathrm{2}{N}_{\mathrm{1}} \mathrm{cos}\:\alpha−{Mg}\:\mathrm{cos}\:\alpha}{\mathrm{2}\:\mathrm{sin}\:\alpha}=\mu{N}_{\mathrm{1}} \:\Rightarrow\:{no}\:{slipping}\:{at}\:\:{point}\:{A}\: \\ $$$$\mathrm{2}{N}_{\mathrm{1}} \left(\mathrm{cos}\:\alpha−\mu\:\mathrm{sin}\:\alpha\right)={Mg}\:\mathrm{cos}\:\alpha \\ $$$$\frac{{MgL}\:\mathrm{cos}\:\alpha+\left(\mathrm{2}{M}+{m}\right){gl}\:\mathrm{cos}\:\beta}{\left({L}\:\mathrm{cos}\:\alpha+{l}\:\mathrm{cos}\:\beta\right)}\left(\mathrm{cos}\:\alpha−\mu\:\mathrm{sin}\:\alpha\right)={Mg}\:\mathrm{cos}\:\alpha \\ $$$$\frac{\mathrm{1}+\lambda\left(\mathrm{2}+\varrho\right)\frac{\mathrm{cos}\:\beta}{\mathrm{cos}\:\alpha}}{\left(\mathrm{1}+\lambda\frac{\mathrm{cos}\:\beta}{\mathrm{cos}\:\vartheta}\right)}\left(\mathrm{1}−\mu\:\mathrm{tan}\:\alpha\right)=\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{1}−\mu\:\mathrm{tan}\:\alpha\right)\left[\mathrm{1}+\left(\mathrm{2}+\varrho\right)\frac{\sqrt{\lambda^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\alpha}}{\mathrm{cos}\:\alpha}\right]=\mathrm{1}+\frac{\sqrt{\lambda^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\alpha}}{\mathrm{cos}\:\alpha}\:\:\:...\left({i}\right) \\ $$$$\Rightarrow\alpha=\alpha_{\mathrm{1}} =... \\ $$$${similarly} \\ $$$${N}_{\mathrm{2}} {l}\:\mathrm{cos}\:\beta−{mg}\frac{{l}\:\mathrm{cos}\:\beta}{\mathrm{2}}−{f}_{\mathrm{2}} {l}\:\mathrm{sin}\:\beta=\mathrm{0} \\ $$$${f}_{\mathrm{2}} =\frac{\mathrm{2}{N}_{\mathrm{2}} \mathrm{cos}\:\beta−{mg}\:\mathrm{cos}\:\beta}{\mathrm{2}\:\mathrm{sin}\:\beta}=\mu{N}_{\mathrm{2}} \:\Rightarrow{no}\:{slipping}\:{at}\:{point}\:{B} \\ $$$$\mathrm{2}{N}_{\mathrm{2}} \left(\mathrm{cos}\:\beta−\mu\:\mathrm{sin}\:\beta\right)={mg}\:\mathrm{cos}\:\beta \\ $$$$\frac{\left({M}+\mathrm{2}{m}\right){gL}\:\mathrm{cos}\:\alpha+{mgl}\:\mathrm{cos}\:\beta}{\left({L}\:\mathrm{cos}\:\alpha+{l}\:\mathrm{cos}\:\beta\right)}\left(\mathrm{cos}\:\beta−\mu\:\mathrm{sin}\:\beta\right)={mg}\:\mathrm{cos}\:\beta \\ $$$$\frac{\left(\mathrm{1}+\mathrm{2}\varrho\right)\frac{\mathrm{cos}\:\alpha}{\mathrm{cos}\:\beta}+\varrho\lambda}{\left(\frac{\mathrm{cos}\:\alpha}{\mathrm{cos}\:\beta}+\lambda\right)}\left(\mathrm{1}−\mu\:\mathrm{tan}\:\beta\right)=\varrho \\ $$$$\Rightarrow\frac{\left(\mathrm{1}+\mathrm{2}\varrho\right)\mathrm{cos}\:\alpha+\varrho\sqrt{\lambda^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\alpha}}{\mathrm{cos}\:\alpha+\sqrt{\lambda^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\alpha}}\left(\mathrm{1}−\frac{\mu\:\mathrm{sin}\:\alpha}{\sqrt{\lambda^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\alpha}}\right)=\varrho\:\:\:...\left({ii}\right) \\ $$$$\Rightarrow\alpha=\alpha_{\mathrm{2}} =... \\ $$$$ \\ $$$$\Rightarrow\alpha={max}\left(\alpha_{\mathrm{1}} ,\alpha_{\mathrm{2}} \right) \\ $$$$\Rightarrow\beta=\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\:\alpha/\lambda\right) \\ $$$$\Rightarrow\theta=\pi−\alpha−\beta \\ $$$$ \\ $$$${Example}:\:\lambda={l}/{L}=\mathrm{0}.\mathrm{75},\:\varrho={m}/{M}=\mathrm{1}.\mathrm{5},\:\mu=\mathrm{0}.\mathrm{5} \\ $$$$\alpha_{\mathrm{1}} =\mathrm{41}.\mathrm{5624}°\:{from}\:\left({i}\right) \\ $$$$\alpha_{\mathrm{2}} =\mathrm{32}.\mathrm{2635}°\:{from}\:\left({ii}\right) \\ $$$$\Rightarrow\alpha=\mathrm{41}.\mathrm{5624}° \\ $$$$\Rightarrow\beta=\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\:\alpha/\lambda\right)=\mathrm{62}.\mathrm{20}° \\ $$$$\Rightarrow\theta_{{max}} =\mathrm{180}−\mathrm{41}.\mathrm{56}−\mathrm{62}.\mathrm{20}=\mathrm{76}.\mathrm{24}° \\ $$
Commented by ajfour last updated on 23/Nov/18

$${Thanks}\:{sir}\:{for}\:{solution}\:{and} \\ $$$${objection}\:{to}\:{my}\:{solution}\:{as}\:{well}. \\ $$
