Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 48250 by ajfour last updated on 21/Nov/18

Commented by ajfour last updated on 21/Nov/18

Find minimum area of △ABC in terms of ellipse parameters a and b.

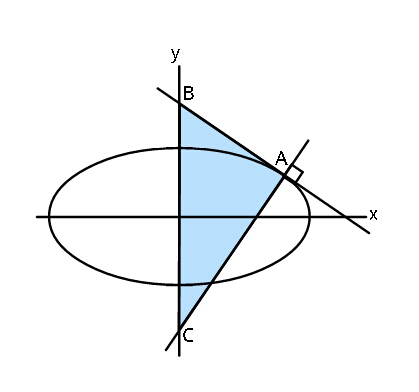
$${Find}\:{minimum}\:{area}\:{of}\:\bigtriangleup{ABC} \\ $$$${in}\:{terms}\:{of}\:{ellipse}\:{parameters} \\ $$$${a}\:{and}\:{b}. \\ $$

Commented by MJS last updated on 21/Nov/18

the minimum area is zero when A= ((0),(b) ) using my beloved coordinate method this leads to a polynome of degree 3 which has got 1 real solution for b<(a/3), 2 real solutions for b=(a/3) and 3 real solutions for b>(a/3). b<a for all cases. will post later

$$\mathrm{the}\:\mathrm{minimum}\:\mathrm{area}\:\mathrm{is}\:\mathrm{zero}\:\mathrm{when}\:{A}=\begin{pmatrix}{\mathrm{0}}\\{{b}}\end{pmatrix} \\ $$$$\mathrm{using}\:\mathrm{my}\:\mathrm{beloved}\:\mathrm{coordinate}\:\mathrm{method}\:\mathrm{this} \\ $$$$\mathrm{leads}\:\mathrm{to}\:\mathrm{a}\:\mathrm{polynome}\:\mathrm{of}\:\mathrm{degree}\:\mathrm{3}\:\mathrm{which}\:\mathrm{has} \\ $$$$\mathrm{got}\:\mathrm{1}\:\mathrm{real}\:\mathrm{solution}\:\mathrm{for}\:{b}<\frac{{a}}{\mathrm{3}},\:\mathrm{2}\:\mathrm{real}\:\mathrm{solutions} \\ $$$$\mathrm{for}\:{b}=\frac{{a}}{\mathrm{3}}\:\mathrm{and}\:\mathrm{3}\:\mathrm{real}\:\mathrm{solutions}\:\mathrm{for}\:{b}>\frac{{a}}{\mathrm{3}}. \\ $$$${b}<{a}\:\mathrm{for}\:\mathrm{all}\:\mathrm{cases}.\:\mathrm{will}\:\mathrm{post}\:\mathrm{later} \\ $$

Commented by ajfour last updated on 21/Nov/18

very interesting sir..

$${very}\:{interesting}\:{sir}.. \\ $$

Answered by ajfour last updated on 21/Nov/18

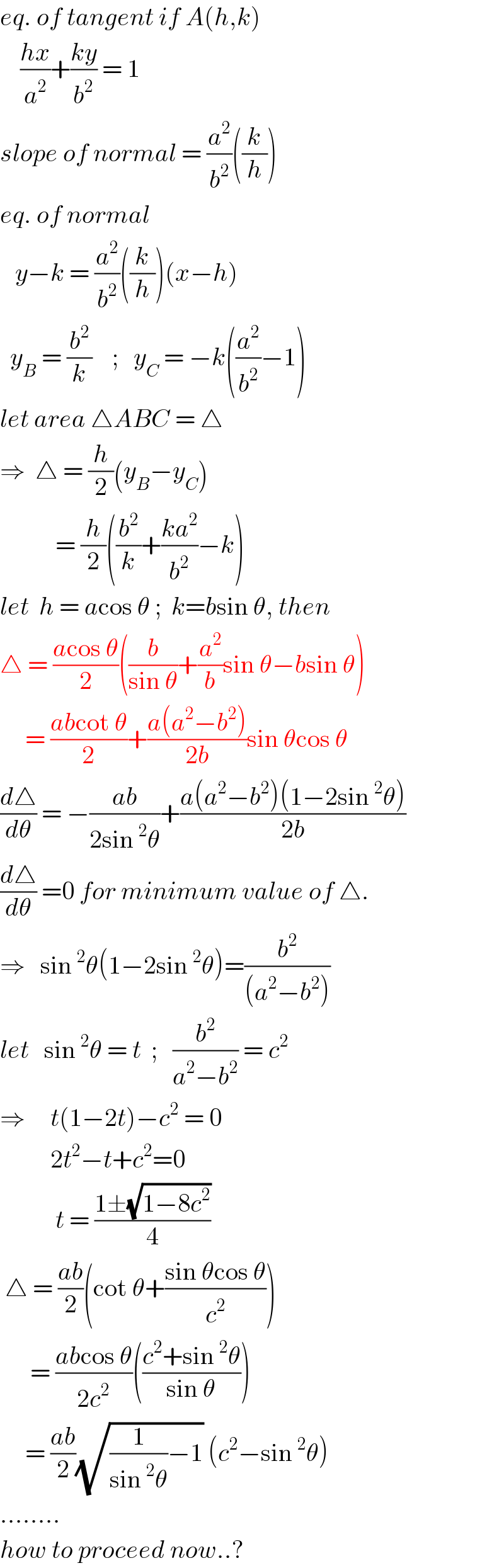
eq. of tangent if A(h,k) ((hx)/a^2 )+((ky)/b^2 ) = 1 slope of normal = (a^2 /b^2 )((k/h)) eq. of normal y−k = (a^2 /b^2 )((k/h))(x−h) y_B = (b^2 /k) ; y_C = −k((a^2 /b^2 )−1) let area △ABC = △ ⇒ △ = (h/2)(y_B −y_C ) = (h/2)((b^2 /k)+((ka^2 )/b^2 )−k) let h = acos θ ; k=bsin θ, then △ = ((acos θ)/2)((b/(sin θ))+(a^2 /b)sin θ−bsin θ) = ((abcot θ)/2)+((a(a^2 −b^2 ))/(2b))sin θcos θ (d△/dθ) = −((ab)/(2sin^2 θ))+((a(a^2 −b^2 )(1−2sin^2 θ))/(2b)) (d△/dθ) =0 for minimum value of △. ⇒ sin^2 θ(1−2sin^2 θ)=(b^2 /((a^2 −b^2 ))) let sin^2 θ = t ; (b^2 /(a^2 −b^2 )) = c^2 ⇒ t(1−2t)−c^2 = 0 2t^2 −t+c^2 =0 t = ((1±(√(1−8c^2 )))/4) △ = ((ab)/2)(cot θ+((sin θcos θ)/c^2 )) = ((abcos θ)/(2c^2 ))(((c^2 +sin^2 θ)/(sin θ))) = ((ab)/2)(√((1/(sin^2 θ))−1)) (c^2 −sin^2 θ) ........ how to proceed now..?

$${eq}.\:{of}\:{tangent}\:{if}\:{A}\left({h},{k}\right) \\ $$$$\:\:\:\:\frac{{hx}}{{a}^{\mathrm{2}} }+\frac{{ky}}{{b}^{\mathrm{2}} }\:=\:\mathrm{1} \\ $$$${slope}\:{of}\:{normal}\:=\:\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\left(\frac{{k}}{{h}}\right) \\ $$$${eq}.\:{of}\:{normal} \\ $$$$\:\:\:{y}−{k}\:=\:\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\left(\frac{{k}}{{h}}\right)\left({x}−{h}\right) \\ $$$$\:\:{y}_{{B}} \:=\:\frac{{b}^{\mathrm{2}} }{{k}}\:\:\:\:;\:\:\:{y}_{{C}} \:=\:−{k}\left(\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\mathrm{1}\right) \\ $$$${let}\:{area}\:\bigtriangleup{ABC}\:=\:\bigtriangleup \\ $$$$\Rightarrow\:\:\bigtriangleup\:=\:\frac{{h}}{\mathrm{2}}\left({y}_{{B}} −{y}_{{C}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{{h}}{\mathrm{2}}\left(\frac{{b}^{\mathrm{2}} }{{k}}+\frac{{ka}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−{k}\right) \\ $$$${let}\:\:{h}\:=\:{a}\mathrm{cos}\:\theta\:;\:\:{k}={b}\mathrm{sin}\:\theta,\:{then} \\ $$$$\bigtriangleup\:=\:\frac{{a}\mathrm{cos}\:\theta}{\mathrm{2}}\left(\frac{{b}}{\mathrm{sin}\:\theta}+\frac{{a}^{\mathrm{2}} }{{b}}\mathrm{sin}\:\theta−{b}\mathrm{sin}\:\theta\right) \\ $$$$\:\:\:\:\:=\:\frac{{ab}\mathrm{cot}\:\theta}{\mathrm{2}}+\frac{{a}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{\mathrm{2}{b}}\mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$$\frac{{d}\bigtriangleup}{{d}\theta}\:=\:−\frac{{ab}}{\mathrm{2sin}\:^{\mathrm{2}} \theta}+\frac{{a}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \theta\right)}{\mathrm{2}{b}} \\ $$$$\frac{{d}\bigtriangleup}{{d}\theta}\:=\mathrm{0}\:{for}\:{minimum}\:{value}\:{of}\:\bigtriangleup. \\ $$$$\Rightarrow\:\:\:\mathrm{sin}\:^{\mathrm{2}} \theta\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \theta\right)=\frac{{b}^{\mathrm{2}} }{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)} \\ $$$${let}\:\:\:\mathrm{sin}\:^{\mathrm{2}} \theta\:=\:{t}\:\:;\:\:\:\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:=\:{c}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:\:{t}\left(\mathrm{1}−\mathrm{2}{t}\right)−{c}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{2}{t}^{\mathrm{2}} −{t}+{c}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{t}\:=\:\frac{\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{8}{c}^{\mathrm{2}} }}{\mathrm{4}} \\ $$$$\:\bigtriangleup\:=\:\frac{{ab}}{\mathrm{2}}\left(\mathrm{cot}\:\theta+\frac{\mathrm{sin}\:\theta\mathrm{cos}\:\theta}{{c}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\:=\:\frac{{ab}\mathrm{cos}\:\theta}{\mathrm{2}{c}^{\mathrm{2}} }\left(\frac{{c}^{\mathrm{2}} +\mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{sin}\:\theta}\right) \\ $$$$\:\:\:\:\:=\:\frac{{ab}}{\mathrm{2}}\sqrt{\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} \theta}−\mathrm{1}}\:\left({c}^{\mathrm{2}} −\mathrm{sin}\:^{\mathrm{2}} \theta\right) \\ $$$$........ \\ $$$${how}\:{to}\:{proceed}\:{now}..? \\ $$

Answered by MJS last updated on 21/Nov/18

I corrected my method. no 3^(rd) degree polynome A= ((p),(((b/a)(√(a^2 −p^2 )))) ) B= ((0),(((ab)/(√(a^2 −p^2 )))) ) C= ((0),((−(((a^2 −b^2 )(√(a^2 −p^2 )))/(ab)))) ) ∣BC∣^2 =(((a^4 −p^2 (a^2 −b^2 ))^2 )/(a^2 b^2 (a^2 −p^2 ))) ∣AC∣^2 =((a^4 −p^2 (a^2 −b^2 ))/b^2 ) ∣AB∣^2 =((p^2 (a^4 −p^2 (a^2 −b^2 )))/(a^2 (a^2 −p^2 ))) Heron′s product gives ((2p(a^4 −p^2 (a^2 −b^2 )))/(ab(√(a^2 −p^2 )))) [and this is zero with p=0] its derivate is ((4(a^2 −b^2 )p^4 −6a^2 (a^2 −b^2 )p^2 +2a^6 )/(ab(√((a^2 −p^2 )^3 )))) zeros are (p>0) p_1 =(a/2)(√(3−((√(a^2 −9b^2 ))/(√(a^2 −b^2 ))))) p_2 =(a/2)(√(3+((√(a^2 −9b^2 ))/(√(a^2 −b^2 ))))) p_1 , p_2 are the local extremes with b<(a/3) with b=(a/3) ⇒ p_1 =p_2 and there′s just a horizontal tangent. with b>(a/3) the area is constantly rising with p towards a the area is zero at p=0 and +∞ at p=a

$$\mathrm{I}\:\mathrm{corrected}\:\mathrm{my}\:\mathrm{method}.\:\mathrm{no}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{degree}\:\mathrm{polynome} \\ $$$${A}=\begin{pmatrix}{{p}}\\{\frac{{b}}{{a}}\sqrt{{a}^{\mathrm{2}} −{p}^{\mathrm{2}} }}\end{pmatrix}\:\:{B}=\begin{pmatrix}{\mathrm{0}}\\{\frac{{ab}}{\sqrt{{a}^{\mathrm{2}} −{p}^{\mathrm{2}} }}}\end{pmatrix}\:\:{C}=\begin{pmatrix}{\mathrm{0}}\\{−\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\sqrt{{a}^{\mathrm{2}} −{p}^{\mathrm{2}} }}{{ab}}}\end{pmatrix} \\ $$$$\mid{BC}\mid^{\mathrm{2}} =\frac{\left({a}^{\mathrm{4}} −{p}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{p}^{\mathrm{2}} \right)}\:\:\mid{AC}\mid^{\mathrm{2}} =\frac{{a}^{\mathrm{4}} −{p}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{{b}^{\mathrm{2}} }\:\:\mid{AB}\mid^{\mathrm{2}} =\frac{{p}^{\mathrm{2}} \left({a}^{\mathrm{4}} −{p}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\right)}{{a}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{p}^{\mathrm{2}} \right)} \\ $$$$\mathrm{Heron}'\mathrm{s}\:\mathrm{product}\:\mathrm{gives} \\ $$$$\frac{\mathrm{2}{p}\left({a}^{\mathrm{4}} −{p}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\right)}{{ab}\sqrt{{a}^{\mathrm{2}} −{p}^{\mathrm{2}} }}\:\:\:\:\:\left[\mathrm{and}\:\mathrm{this}\:\mathrm{is}\:\mathrm{zero}\:\mathrm{with}\:{p}=\mathrm{0}\right] \\ $$$$\mathrm{its}\:\mathrm{derivate}\:\mathrm{is} \\ $$$$\frac{\mathrm{4}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){p}^{\mathrm{4}} −\mathrm{6}{a}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){p}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{6}} }{{ab}\sqrt{\left({a}^{\mathrm{2}} −{p}^{\mathrm{2}} \right)^{\mathrm{3}} }} \\ $$$$\mathrm{zeros}\:\mathrm{are}\:\left({p}>\mathrm{0}\right) \\ $$$${p}_{\mathrm{1}} =\frac{{a}}{\mathrm{2}}\sqrt{\mathrm{3}−\frac{\sqrt{{a}^{\mathrm{2}} −\mathrm{9}{b}^{\mathrm{2}} }}{\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}}\:\:{p}_{\mathrm{2}} =\frac{{a}}{\mathrm{2}}\sqrt{\mathrm{3}+\frac{\sqrt{{a}^{\mathrm{2}} −\mathrm{9}{b}^{\mathrm{2}} }}{\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}} \\ $$$${p}_{\mathrm{1}} ,\:{p}_{\mathrm{2}} \:\mathrm{are}\:\mathrm{the}\:\mathrm{local}\:\mathrm{extremes}\:\mathrm{with}\:{b}<\frac{{a}}{\mathrm{3}} \\ $$$$\mathrm{with}\:{b}=\frac{{a}}{\mathrm{3}}\:\Rightarrow\:{p}_{\mathrm{1}} ={p}_{\mathrm{2}} \:\mathrm{and}\:\mathrm{there}'\mathrm{s}\:\mathrm{just}\:\mathrm{a}\:\mathrm{horizontal} \\ $$$$\mathrm{tangent}.\:\mathrm{with}\:{b}>\frac{{a}}{\mathrm{3}}\:\mathrm{the}\:\mathrm{area}\:\mathrm{is}\:\mathrm{constantly} \\ $$$$\mathrm{rising}\:\mathrm{with}\:{p}\:\mathrm{towards}\:{a} \\ $$$$\mathrm{the}\:\mathrm{area}\:\mathrm{is}\:\mathrm{zero}\:\mathrm{at}\:{p}=\mathrm{0}\:\mathrm{and}\:+\infty\:\mathrm{at}\:{p}={a} \\ $$

Commented by ajfour last updated on 21/Nov/18

thanks for the correct vision, Sir.

$${thanks}\:{for}\:{the}\:{correct}\:{vision},\:{Sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com