
Question Number 48196 by ajfour last updated on 20/Nov/18
Commented by ajfour last updated on 20/Nov/18

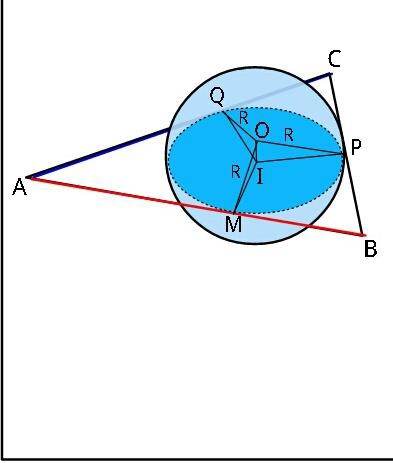
$${Find}\:{volume}\:{of}\:{sphere}\:{above} \\ $$$${the}\:{triangular}\:{plane}\:{in}\:{terms} \\ $$$${of}\:\:\boldsymbol{{a}},\:\boldsymbol{{b}},\:\boldsymbol{{c}},\:{and}\:\boldsymbol{{R}}. \\ $$
Answered by mr W last updated on 20/Nov/18
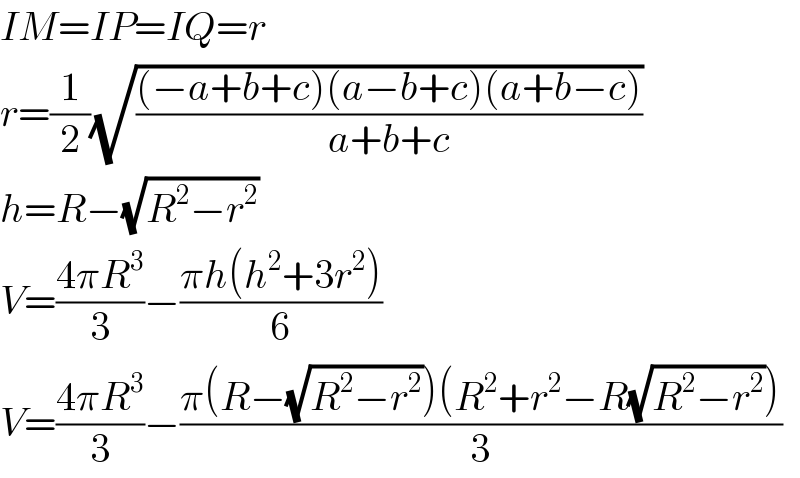
$${IM}={IP}={IQ}={r} \\ $$$${r}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}{{a}+{b}+{c}}} \\ $$$${h}={R}−\sqrt{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$${V}=\frac{\mathrm{4}\pi{R}^{\mathrm{3}} }{\mathrm{3}}−\frac{\pi{h}\left({h}^{\mathrm{2}} +\mathrm{3}{r}^{\mathrm{2}} \right)}{\mathrm{6}} \\ $$$${V}=\frac{\mathrm{4}\pi{R}^{\mathrm{3}} }{\mathrm{3}}−\frac{\pi\left({R}−\sqrt{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }\right)\left({R}^{\mathrm{2}} +{r}^{\mathrm{2}} −{R}\sqrt{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }\right)}{\mathrm{3}} \\ $$
Commented by ajfour last updated on 21/Nov/18
$${Thanks}\:{sir},\:{this}\:{shall}\:{be}\:{very} \\ $$$${helpful}\:{to}\:{me}. \\ $$
