
Question Number 48091 by peter frank last updated on 19/Nov/18

Commented by maxmathsup by imad last updated on 19/Nov/18
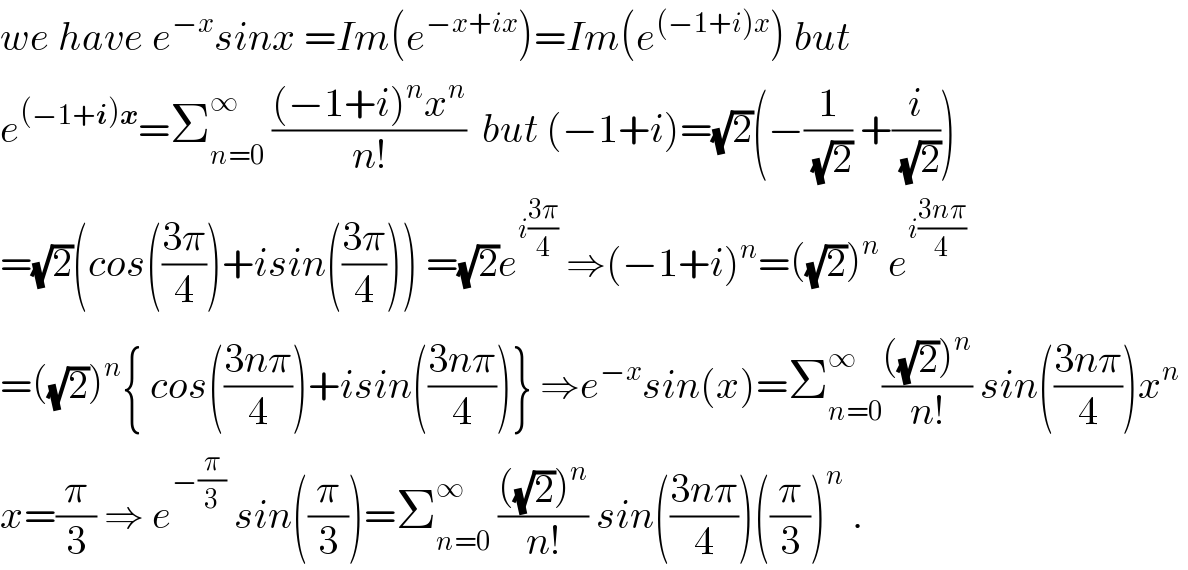
$${we}\:{have}\:{e}^{−{x}} {sinx}\:={Im}\left({e}^{−{x}+{ix}} \right)={Im}\left({e}^{\left(−\mathrm{1}+{i}\right){x}} \right)\:{but} \\ $$$${e}^{\left(−\mathrm{1}+\boldsymbol{{i}}\right)\boldsymbol{{x}}} =\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}+{i}\right)^{{n}} {x}^{{n}} }{{n}!}\:\:{but}\:\left(−\mathrm{1}+{i}\right)=\sqrt{\mathrm{2}}\left(−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:+\frac{{i}}{\sqrt{\mathrm{2}}}\right) \\ $$$$=\sqrt{\mathrm{2}}\left({cos}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)+{isin}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)\right)\:=\sqrt{\mathrm{2}}{e}^{{i}\frac{\mathrm{3}\pi}{\mathrm{4}}} \:\Rightarrow\left(−\mathrm{1}+{i}\right)^{{n}} =\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{e}^{{i}\frac{\mathrm{3}{n}\pi}{\mathrm{4}}} \\ $$$$=\left(\sqrt{\mathrm{2}}\right)^{{n}} \left\{\:{cos}\left(\frac{\mathrm{3}{n}\pi}{\mathrm{4}}\right)+{isin}\left(\frac{\mathrm{3}{n}\pi}{\mathrm{4}}\right)\right\}\:\Rightarrow{e}^{−{x}} {sin}\left({x}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\left(\sqrt{\mathrm{2}}\right)^{{n}} }{{n}!}\:{sin}\left(\frac{\mathrm{3}{n}\pi}{\mathrm{4}}\right){x}^{{n}} \: \\ $$$${x}=\frac{\pi}{\mathrm{3}}\:\Rightarrow\:{e}^{−\frac{\pi}{\mathrm{3}}} \:{sin}\left(\frac{\pi}{\mathrm{3}}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(\sqrt{\mathrm{2}}\right)^{{n}} }{{n}!}\:{sin}\left(\frac{\mathrm{3}{n}\pi}{\mathrm{4}}\right)\left(\frac{\pi}{\mathrm{3}}\right)^{{n}} \:. \\ $$
Commented by peter frank last updated on 19/Nov/18

$$\mathrm{thanks}\: \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 19/Nov/18

$${p}={e}^{−{x}} {cosx} \\ $$$${q}={e}^{−{x}} {sinx} \\ $$$${p}+{iq}={e}^{−{x}} \left({cosx}+{isinx}\right)={e}^{−{x}} .{e}^{{ix}} ={e}^{{x}\left(−\mathrm{1}+{i}\right)} ={e}^{{tx}} \\ $$$${e}^{{tx}} =\mathrm{1}+{tx}+\frac{{t}^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{t}^{\mathrm{3}} {x}^{\mathrm{3}} }{\mathrm{3}!}+... \\ $$$$=\mathrm{1}+\left(−\mathrm{1}+{i}\right){x}+\left(−\mathrm{1}+\mathrm{i}\right)^{\mathrm{2}} ×\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\left(−\mathrm{1}+{i}\right)^{\mathrm{3}} ×\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:{other} \\ $$$${terms}\:{not}\:{considered}\:{as}\:{to}\:{find}\:{coefficient}\:{of} \\ $$$${upto}\:{x}^{\mathrm{3}} \\ $$$$=\mathrm{1}+\left(−{x}+{ix}\right)+\left(−{ix}^{\mathrm{2}} \right)+\left(−\mathrm{2}{i}\right)\left(−\mathrm{1}+{i}\right)×\frac{{x}^{\mathrm{3}} }{\mathrm{3}!} \\ $$$$=\mathrm{1}+\left(−{x}+{ix}\right)+\left(−{ix}^{\mathrm{2}} \right)+\left(\mathrm{2}{i}+\mathrm{2}\right)\frac{{x}^{\mathrm{3}} }{\mathrm{6}} \\ $$$$=\left(\mathrm{1}−{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)+{i}\left({x}−{x}^{\mathrm{2}} +\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right) \\ $$$${so}\:{e}^{{tx}} ={e}^{\left(−\mathrm{1}+{i}\right){x}} =\left(\mathrm{1}−{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)+{i}×\frac{{x}}{\mathrm{3}}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right) \\ $$$${e}^{−{x}} ×{e}^{{ix}} =\left(\mathrm{1}−{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)+{i}×\frac{{x}}{\mathrm{3}}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right) \\ $$$${e}^{−{x}} \left({cosx}+{isinx}\right)=\left(\mathrm{1}−{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)+{i}×\frac{{x}}{\mathrm{3}}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right) \\ $$$${hence} \\ $$$${e}^{−{x}} {sinx}=\frac{{x}}{\mathrm{3}}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)\:\:{proved} \\ $$$${e}^{−\frac{\pi}{\mathrm{3}}} {sin}\left(\frac{\pi}{\mathrm{3}}\right)=\frac{\pi}{\mathrm{9}}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{9}}−\pi+\mathrm{3}\right) \\ $$
