
Question Number 48050 by ajfour last updated on 18/Nov/18
Commented by ajfour last updated on 18/Nov/18

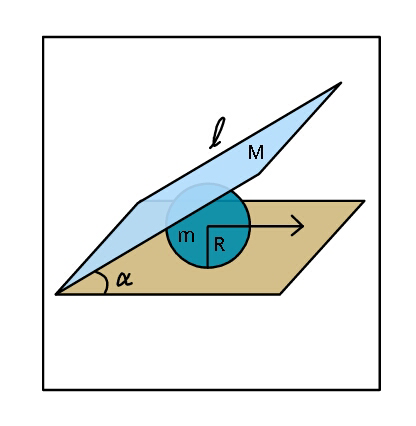
$${Find}\:{acceleration}\:{of}\:{sphere}\:{and} \\ $$$${angular}\:{velocity}\:{of}\:{plank}\:{as}\:{a} \\ $$$${function}\:{of}\:{a}\:{subsequent}\:{angle}\:\theta. \\ $$$${Assume}\:{all}\:{surfaces}\:{frictionless} \\ $$$${and}\:{figure}\:{depicts}\:{the}\:{initial} \\ $$$${situation}\:{when}\:{system}\:{is}\:{released} \\ $$$${at}\:{rest}. \\ $$
Answered by mr W last updated on 19/Nov/18
Commented by mr W last updated on 19/Nov/18
![v=(dx/dt), ω=(dθ/dt) x tan (θ/2)=R v tan (θ/2)+x (ω/(2 cos^2 (θ/2)))=0 v tan^2 (θ/2)+((ωR)/(2 cos^2 (θ/2)))=0 v sin^2 (θ/2)+((ωR)/2)=0 ⇒ω=−((2v sin^2 (θ/2))/R)=(((cos θ−1)v)/R) ((mv^2 )/2)+((Iω^2 )/2)=((MgL(sin α−sin θ))/2) mv^2 +((ML^2 )/3)×((v^2 (cos θ−1)^2 )/R^2 )=MgL(sin α−sin θ) let κ=(m/M), λ=(L/R) [κ+((λ^2 (cos θ−1)^2 )/3)]v^2 =gL(sin α−sin θ) v^2 =((gL(sin α−sin θ))/(κ+((λ^2 (cos θ−1)^2 )/3))) ⇒v=(√((gL(sin α−sin θ))/(κ+((λ^2 (cos θ−1)^2 )/3)))) ⇒ω=((cos θ−1)/R)(√((gL(sin α−sin θ))/(κ+((λ^2 (cos θ−1)^2 )/3)))) a=(dv/dt)=ω(dv/dθ)=......](Q48088.png)
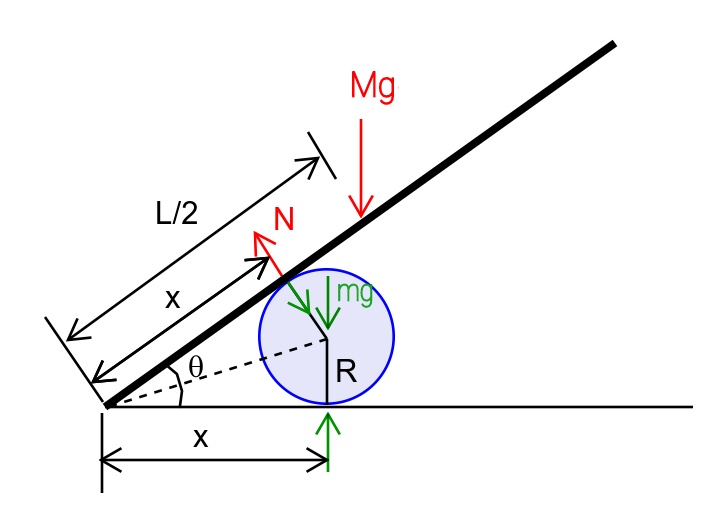
$${v}=\frac{{dx}}{{dt}},\:\omega=\frac{{d}\theta}{{dt}} \\ $$$${x}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}={R} \\ $$$${v}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}+{x}\:\frac{\omega}{\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}=\mathrm{0} \\ $$$${v}\:\mathrm{tan}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}+\frac{\omega{R}}{\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}=\mathrm{0} \\ $$$${v}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}+\frac{\omega{R}}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow\omega=−\frac{\mathrm{2}{v}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}{{R}}=\frac{\left(\mathrm{cos}\:\theta−\mathrm{1}\right){v}}{{R}} \\ $$$$\frac{{mv}^{\mathrm{2}} }{\mathrm{2}}+\frac{{I}\omega^{\mathrm{2}} }{\mathrm{2}}=\frac{{MgL}\left(\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta\right)}{\mathrm{2}} \\ $$$${mv}^{\mathrm{2}} +\frac{{ML}^{\mathrm{2}} }{\mathrm{3}}×\frac{{v}^{\mathrm{2}} \left(\mathrm{cos}\:\theta−\mathrm{1}\right)^{\mathrm{2}} }{{R}^{\mathrm{2}} }={MgL}\left(\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta\right) \\ $$$${let}\:\kappa=\frac{{m}}{{M}},\:\lambda=\frac{{L}}{{R}} \\ $$$$\left[\kappa+\frac{\lambda^{\mathrm{2}} \left(\mathrm{cos}\:\theta−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{3}}\right]{v}^{\mathrm{2}} ={gL}\left(\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta\right) \\ $$$${v}^{\mathrm{2}} =\frac{{gL}\left(\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta\right)}{\kappa+\frac{\lambda^{\mathrm{2}} \left(\mathrm{cos}\:\theta−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{3}}} \\ $$$$\Rightarrow{v}=\sqrt{\frac{{gL}\left(\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta\right)}{\kappa+\frac{\lambda^{\mathrm{2}} \left(\mathrm{cos}\:\theta−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{3}}}} \\ $$$$\Rightarrow\omega=\frac{\mathrm{cos}\:\theta−\mathrm{1}}{{R}}\sqrt{\frac{{gL}\left(\mathrm{sin}\:\alpha−\mathrm{sin}\:\theta\right)}{\kappa+\frac{\lambda^{\mathrm{2}} \left(\mathrm{cos}\:\theta−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{3}}}} \\ $$$${a}=\frac{{dv}}{{dt}}=\omega\frac{{dv}}{{d}\theta}=...... \\ $$
Commented by ajfour last updated on 19/Nov/18
$${Too}\:{Good},\:{Sir}!\:{I}\:{will}\:{also}\:{try}.. \\ $$
